变破产下限相依风险比例再保险的风险模型

雷 鸣，陈新美

（长沙理工大学数学与计算科学学院，长沙410114）

保险业是经营风险的特殊金融服务行业，同时自身的经营又面临风险。再保险是一种分散保险公司风险的有效方法，而破产概率又是度量风险的重要指标。根据保险公司的实际情况建立有再保险因素的风险模型，研究再保险对破产概率的影响是保险数学中的一个重要的研究课题。文献[1]对经典模型加以推广，得到带稀疏过程的风险模型

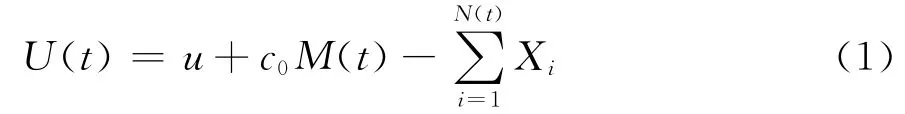
式中：u——u＞0是初始准备金；

c0——c0＞0是保单的平均保费；

M（t）——是到时刻t为止保险公司售出的保单数，且是参数为λ的齐次Poisson过程；

N（t）——是到时刻t为止保险公司理赔的保单数，N（t）是M（t）的p－稀疏过程（0＜p＜1）。

本文对模型（1）加以推广并考虑变破产下限的问题。

1 模型描述

给定一完备概率空间（Ω，F，P），所有涉及的随机过程和随机变量都定义在此概率空间上，考虑风险模型：

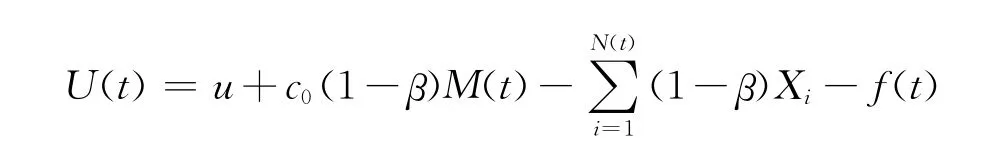
式中：u——初始准备金；

c0——每张保单的平均保费；

M（t）——到时刻t为止保险公司售出的保单数；

N（t）——到时刻t为止保险公司理赔的保单数；

Xi—— 第i次的索赔额，且｛Xi，i＝1，2，…｝是非负独立同分布的随机变量序列，设其分布函数为F（x）；

f（t）—— 变破产下限，f（t）是非负的；

β——再保险比例。

假设｛M（t），t≥0｝是参数为λ的齐次Poisson过程，｛N（t），t≥0｝是｛M（t），t≥0｝的p－稀疏过程，其中0＜p＜1，不妨记｛N（t），t≥0｝这一过程为｛M（t，p），t≥0｝，这里为了方便计算我们假设f（t）是线性的，记

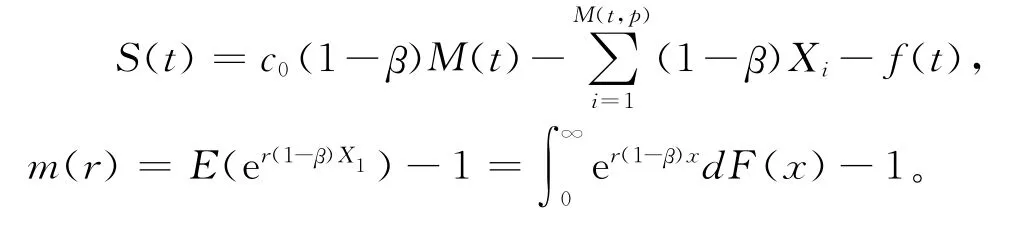
2 预备引理

引理1 盈利过程｛S（t），t≥0｝具有以下性质：

（1）｛S（t），t≥0｝具有平稳独立增量性；

（2）为了保证保险公司的稳定经营，我们假设E[S（t）]＞0。

引理2为Ft的鞅，其中

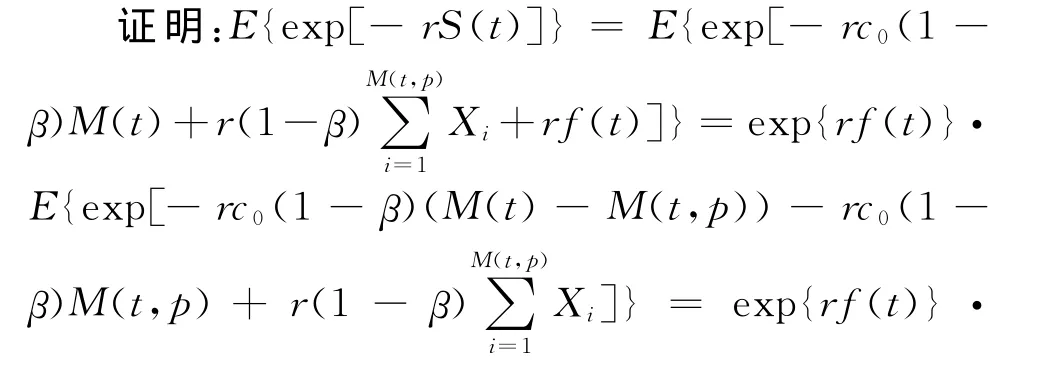
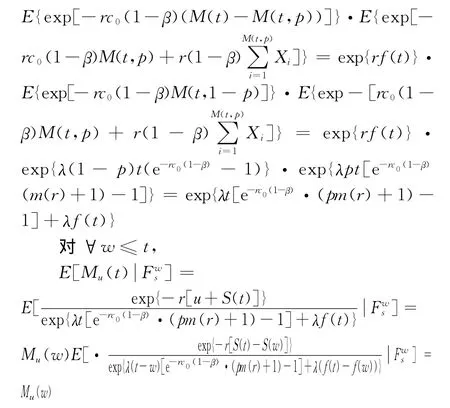
3 主要结果

定义1 破产时刻；破产概率Ψ（u）＝P｛Tu＜ ∞｝。

定理1 破产概率满足不等式：Ψ（u）≤e－ruH（r），其 中

证明：设t0＜∞为一常数，由于Tu是破产时刻，则t0∧Tu为有界停时，根据引理和停时定理可得：

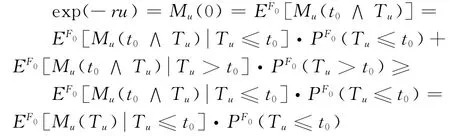
从而

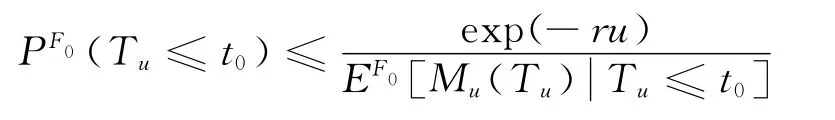
而

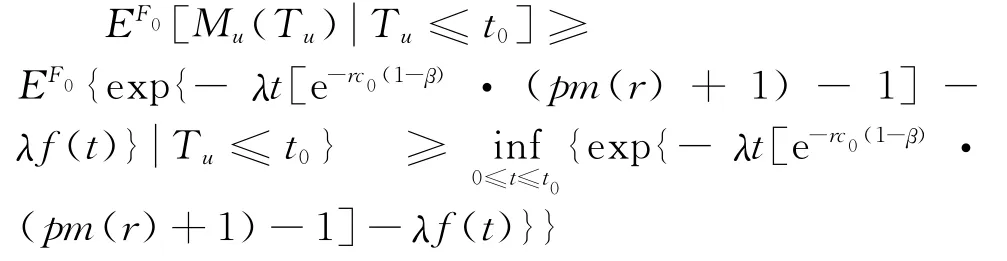
所以

PF0（Tu≤t0）≤（pm（r）＋1）－1]＋λf（t）｝｝两边取期望且令t0→∞得：Ψ（u）≤e－ru·H（r）

由于假设f（t）为线性，这里讨论f（t）的具体形式。

定理2 当f（t）＝a＋bt时，U（t）＝u－a－

（1）破产概率满足等式：

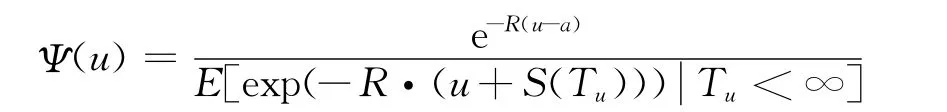
（2）破产概率满足不等式：

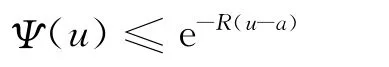
其中R 为关于r 的方程λ[e－rc0（1－β）·（pm（r）＋1）－1]＋rb＝0的解。

定理2的证明与文献[6]定理2证明类似。

[1]陈珊萍，王过京，王振羽.稀疏过程在保险公司破产问题中的应用[J].数学统计与管理，2001，20（5）：26－30.

[2]陈占斌，刘再明.稀疏过程在破产问题中的应用[J].数学理论与应用，2005，25（1）：35－38.

[3]马学思，刘次华.变破产下限风险模型的破产概率[J].数理统计与管理，2007，26（3）：440－443.

[4]王变，张馨方.变破产下限风险再保险模型的破产概率[J].现代商贸工业，2010，（8）：137.

[5]邓永录，梁之舜.随机点过程及其应用[M].北京：科学出版社，1998：1－115.

[6]张馨方，成军祥，王涛.变破产下限双Poisson风险模型的破产概率[J].现代商贸工业，2010，（7）：154.

[7]钱敏平，龚光鲁.随机过程论[M].北京：北京大学出版社，1997：411－415.

[8]张茂军，南江霞，夏尊铨.随机过程论[J].高校应用数学学报，2007，22（4）：411－415.

[9]花俊，陈新美.稀疏过程在变破产下限风险模型中的应用[J].长春工程学院院报：自然科学版，2011，12（1）：142－144.