基于有限元的数控机床床身筋板的动态性能分析与优化设计

杨明亚，杨 涛，王 芳，张长泉，卢灿举，杨颖洁

（1.安徽新闻出版职业技术学院，合肥230601；2.内蒙古工业大学，呼和浩特010051；3.解放军电子工程学院，合肥230037；4.苏州德胜电机有限公司，苏州215122）

0 引言

要进行机床床身结构的动态性能分析，首先必需建立一个真正反映振动系统实际情况的动力学模型和对应的数学模型，它是整个模态分析过程最基本的问题。模型建立得准确与否，将直接影响分析的结果。根据数学模型求解系统的特征向量初特征值（主振型和固有频率）。

一个N自由度线形系统，其运动微分方程为[1－2]：

式中：M，C，K——为系统的质量、阻尼、刚度矩阵；

F——激励力向量矩阵。

求解F＝0时的齐次方程，得到方程的通解将反映系统的自由振动特性，求解它所对应的特征方程得到系统特征解将反映结构的固有特性。

求解F≠0时的非齐次方程，得到方程的特解将反映输入载荷的持点。

固有频率和主振型是振动系统的自然属性，必需通过研究无阻尼的自由振动来求解，假定有一具有N个自由度的多自由度振动系统，它的无阻尼自由振动运动方程为：

此方程要解耦后求解，因线性振动的振动位移是简谐振动函数，根据高等数学知识可得此解的形式必为：

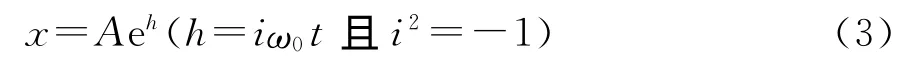
代入式（2）消去eh，整理得

由线性代数知识知A非零解的条件是式（4）的系数行列式应满足：

A为系统的振幅列阵，ω0为固有频率。

通过式（5）可求得固有频率ω0，将其代入式（4）可求得A。一般情况下振动系统具有N个自由度，就有N个固有频率ω01，ω02，…，ω0n，以及N 个对应的主振型A（1），A（2），…，A（n）。

每一阶固有频率对应一阶主振型，倘若第r阶固有频率ω0r已知，带入：（k－m）A＝0展开为[3]：

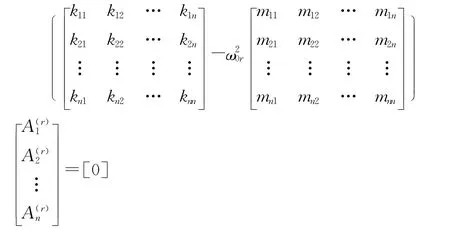
写成方程的形式：

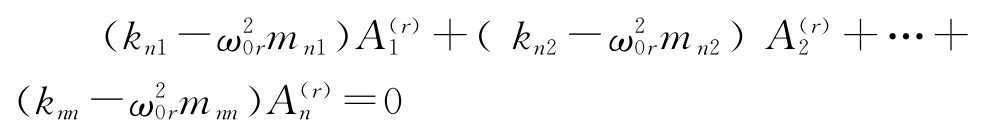
上式是振动系统第r阶主振型且A（r）的n元方程组，解方程组可以得到系统在以ω0r频率振动时的主振型：

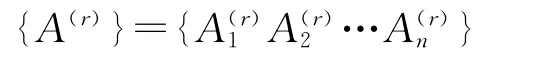
每一阶固有频率有—阶对应的主振型，整个系统全部固有频率所对应的全部主振型集合起来便是系统的主振型。

这就进一步说明了固有频率与主振型是振动系统最基本的固有属性，不会随意改变，这种振动系统中的固有属性，只有在被激励时才表现出来，这就是动态响应。

1 床身结构有限元模型的建立

用Pro／ENGINEER建立机床床身的三维实体模型，因其比ANASYS建模更方便、快捷，特别是建立机床床身这样复杂的三维实体模型，需要耗费大量的时间和精力，所以用Pro／ENGINEER软件可以提高建立实体模型的效率。建好三维模型后再导入ANSYS中，床身的动态性能分析在有限元分析软件ANSYS上进行。由于机床的床身内部是由筋板加强的，筋板的数量影响床身的动态性能。下面就从改变筋板的数量来分析其动态性能并进行优化设计。为了叙述方便把横向筋板定义为短筋板，纵向的则定义为长筋板，下面就开始分析筋板与床身频率之间的关系，并进行结构优化。

用Pro／ENGINEER软件建模的机床床身的尺寸如下[3]：

图1 机床床身外形图

2 筋板数量的改变与固有频率的关系

根据简化后的床身进行优化，找出最优解。为便于说明进行以下的定义，以图2为例进行定义，中间的一条筋板定义为纵向筋板，宽度方向的四块筋板定义为横向筋板，高度方向上的2块筋板定义为高度筋板，图2的筋板记作：1×4×2型筋板。

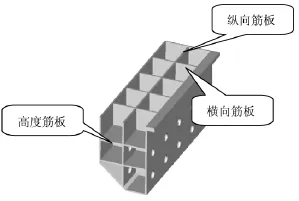
图2 1×4×2型筋板床身图

下面就在ANSYS软件中进行计算，分析这种形式的筋板，得出其固有频率，并与其他类型的筋板分析比较。

由于床身的振动可以表达为各阶固有振型的线性组合，其中低阶固有振型要比高阶对床身的振动影响大，越是低阶影响就越大，因此低阶振型对床身的动态特性起决定作用，故进行床身的振动特性的分析计算时通常取前1～5阶。经过有限元计算得出其固有频率如图3所示[4]。

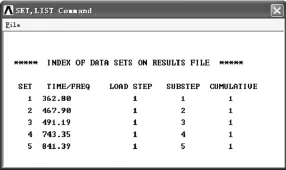
图3 1×4×2型筋板床身固有频率图

（1）床身增加一块纵向的筋板如图4，筋板型式记作：2×4×2型。

图4 2×4×2型筋板床身图

计算固有频率如图5所示。

图5 2×4×2型筋板床身固有频率图

从上面2种形式的筋板布置可以看出，纵向筋板的数量的增加，并不能提高床身的一阶固有频率，从1块纵向筋板到2块纵向筋板，其一阶固有频率分别为：362.80Hz，和348.67Hz，可以看出频率的变化趋势是下降的。从节省材料，优化设计的观点出发，采用1块纵向筋板作为最优的设计方案。

（2）既然纵向筋板数量的增加，致使固有频率不增反降，那么就增加横向筋板的数量，计算其固有频率。增加一块横行的筋板，那么横向筋板的数量增加至5块，如图6，筋板的型式记作：1×5×2型。

图6 1×5×2型筋板床身图

计算出的固有频率如图7所示。

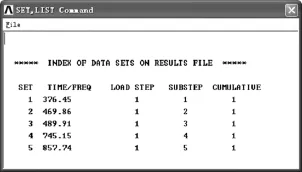
图7 1×5×2型筋板床身固有频率图

由此可见横向筋板的增加会提高床身的动态特性。

（3）增加2块横行的筋板，那么横向筋板的数量增加至6块，如图8，筋板的型式记作：1×6×2型。

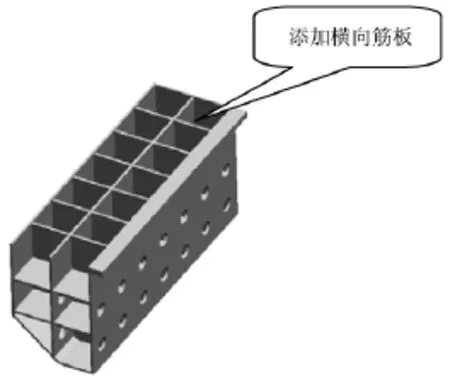
图8 1×6×2型筋板床身图

计算出的固有频率如图9所示。

图9 1×6×2型筋板床身固有频率图

随着横向筋板数量的增加，频率是增加的，从4块筋板时的362.8Hz，5块筋板时的376.45Hz，到6块筋板时的390.92Hz，可见横行筋板数量的增加会提高床身的动态性能。床身的总长度为2 045mm，若用4块筋板，则筋板间的距离为2 045／5＝409mm，若用5块筋板，则筋板间的距离为2 045／6≈341mm，若用6块筋板，则筋板间的距离为2 045／7≈292mm，设计时要从多方面考虑进行优化设计，如果床身的固有频率足够高，那么床身的动、静刚度能够满足刚度的设计要求即可。

3 筋板的厚度与床身固有频率的关系及优化

如果改变筋板的厚度，以1×4×2型筋板的床身为研究对象，壁厚和筋板厚度均为20mm时，计算的结果如下：

把筋板由原来的20mm改为18mm，计算的结果如下：

把筋板由原来的20mm改为16mm，计算的结果如下：

把筋板由原来的20mm改为15mm，计算的结果如下：

把筋板由原来的20mm改为14mm，计算的结果如下：

可见筋板厚度的减小会使床身的一阶固有频率下降，下降的速度如图10所示。二阶固有频率变化曲线如图11所示。

图10 一阶固有频率变化曲线

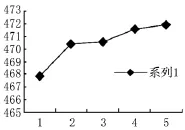
图11 二阶固有频率变化曲线

从频率曲线图可以看出一阶频率是随着筋板厚度的减小固有频率是下降的，而二阶以上的频率变化并非如一阶频率的变化，在频率的变化曲线图能看出或上升或下降，当筋板为18mm时，一阶频率从362.80Hz到359.20Hz是下降的，二阶频率从467.90Hz到470.35Hz是上升的，在四阶固有频率变化曲线图可以看出，筋板为18mm时是一个转折点，从优化设计的角度出发，综合前五阶的频率变化曲线图，当壁厚为20mm时筋板应选择18mm。

4 结语

从上述的分析可以看出有的筋板数量的增加，并不能提高床身的振动频率，这就要求我们在设计机床时不能盲目地增加筋板的数量，在设计筋板时一定要有科学的指导。增加纵向筋板的数量，床身的一阶固有频率不升反降，但是横向筋板数量的增加可以提高床身的振动频率，可见横行筋板数量的增加会提高床身的动态性能。筋板厚度的增加也可以提高床身的振动频率，但是厚度的增加会使其重量增加，从优化设计的角度出发可以选择适当的筋板的厚度。

[1]杨橚，唐恒龄.机床动力学（Ⅱ）[M].北京：机械工业出版社，1983：1－20.

[2]李东旭.高等机构动力学[M].长沙：国防科技大学出版社，1997：2－3.

[3]何博.中文Pro／ENGINEERWildfire速成教程 [M].北京：中国电力出版社，2004：1－243.

[4]张朝晖.ANSYS8.0结构分析及实例解析[M].北京：机械工业出版社，2005：181－220.