双参数二阶非线性周期边值问题Green函数与正解

张 丽

(黑龙江八一农垦大学文理学院,大庆163319)

0 引言

非线性微分方程周期边值问题在数学物理领域中具有深刻实际的背景,其正解存在性研究无论在理论上还是在应用中都有非常重要的意义。关于含参数二阶非线性周期边值问题,一些作者对正解存在性也有过研究,例如文[1—6]。本文借鉴了文献[7—8]的结论,采用范数形式的锥不动点定理研究了一类含双参数二阶非线性周期边值正解存在性。

1 问题假设与主要定理

本部分研究二阶非线性周期边值问题

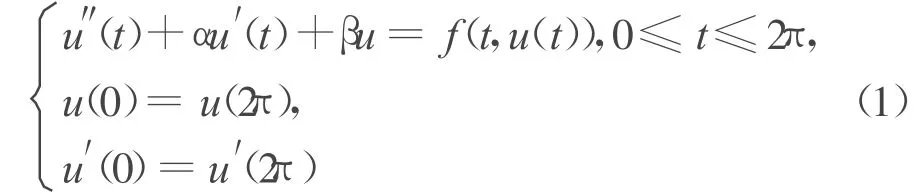
正解的存在性,其中 α＜0,0＜4β-α2＜1。

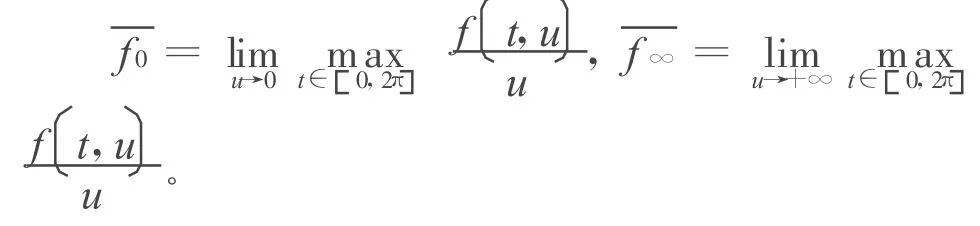
假设如下:

定理1 假设或者成立,则边值问题(1)至少存在一个正解。

从定理1,可得如下

推论1 若方程(1)满足及以下情形之一:

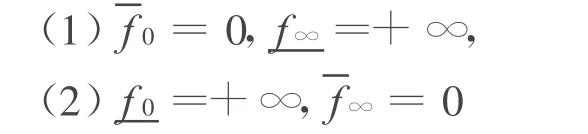
则边值问题(1)至少存在一个正解。

引理1[8]若r(t)是线性周期边值问题

的解,则(1)的解为

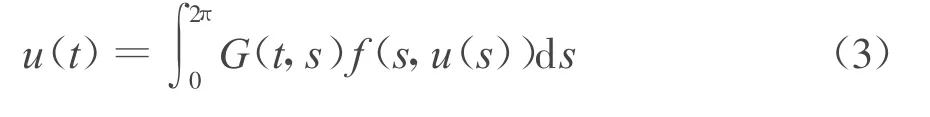
其中

引理2 线性周期边值问题(1)的解r(t)形式如下

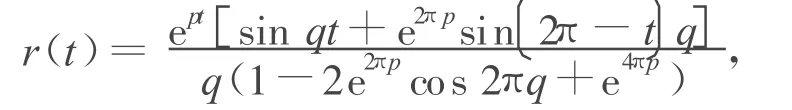
证明:其特征方程 λ2+α λ+β=0

Δ=α2-4β,当 α＜0,0 ＜4β-α2＜1时,

且有

将边值条件 r(0)=r(2π),r′(0)-r′(2π)=1带入式(5)和式(6)

得到:

由克莱姆法则得:

由引理1可知问题(1)等价于下述的积分方程

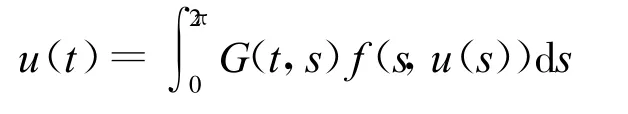
其中

易知G(t,s)＞0。

引理3 对任意的成立0＜m ≤G(t,s)≤M,

其中

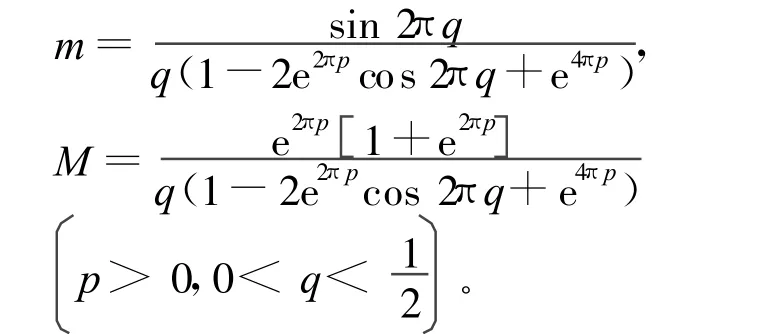
定义映射

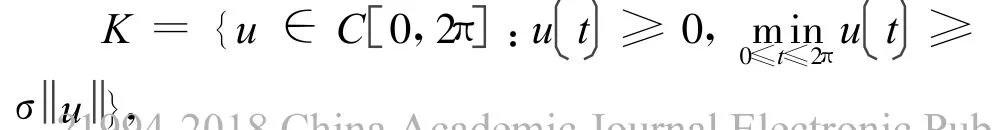
其中

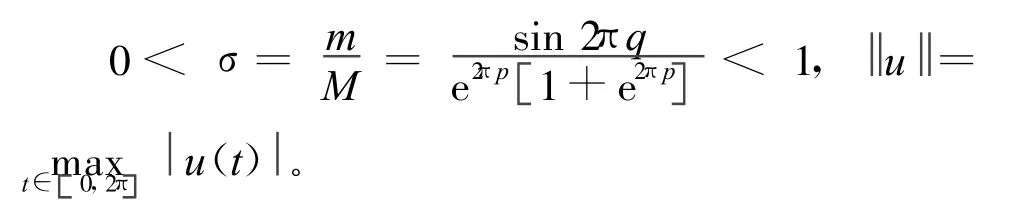
容易知道 ∀u∈K,

引理4 Φ:K→K是全连续算子。

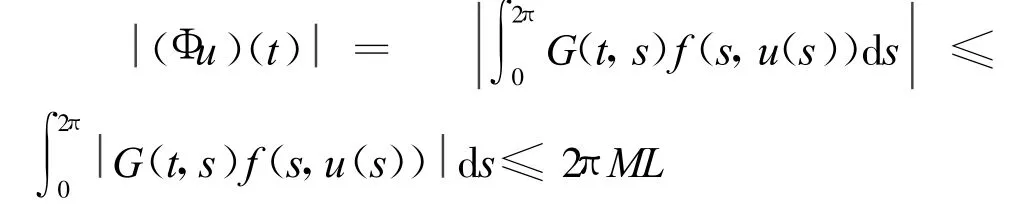
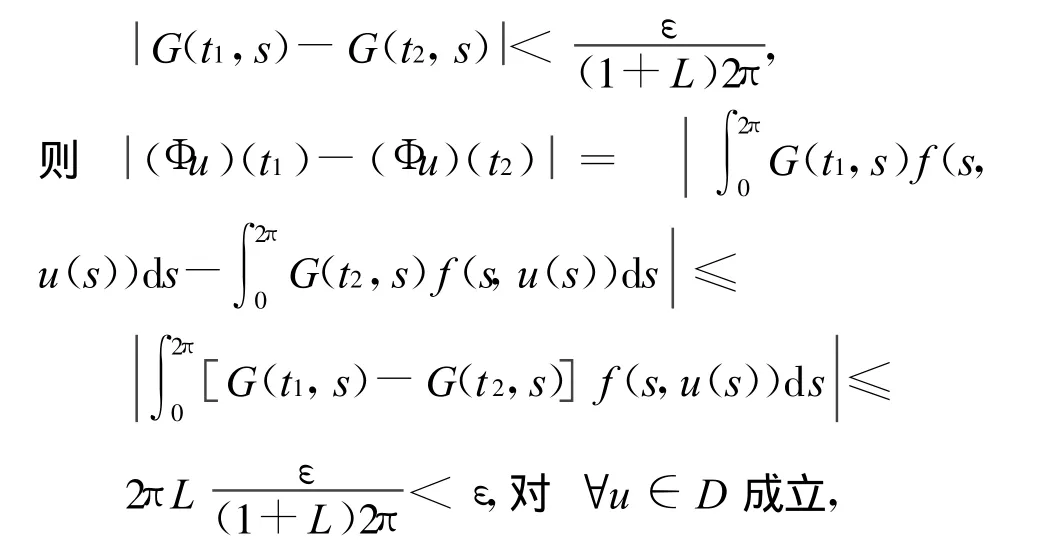
再证 Φ是连续算子。

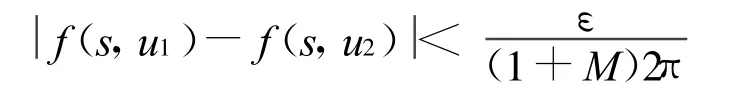
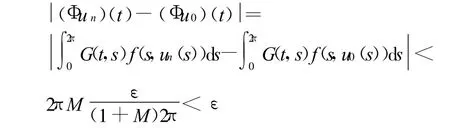
2 主要定理的证明

设E是Banach空间,K⊂E是E中的一个闭锥,Ω是E中的开集,其边界记为。令是全连续算子,若定义不动点指数若则Φ在K ∩Ω上有一个不动点[8]。

引理5[8]令 Φ:K →K是全连续算子,若 μ Φ u ≠u,∀u ∈ ∂Kr,0＜μ≤1,则有 i(Φ,Kr,K)=1。

引理6[8]令Φ:K →K是全连续算子,若满足以下2个条件:

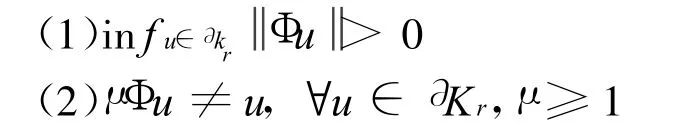
则有i(Φ,Kr,K)=0。

证明定理1:

情形(1):

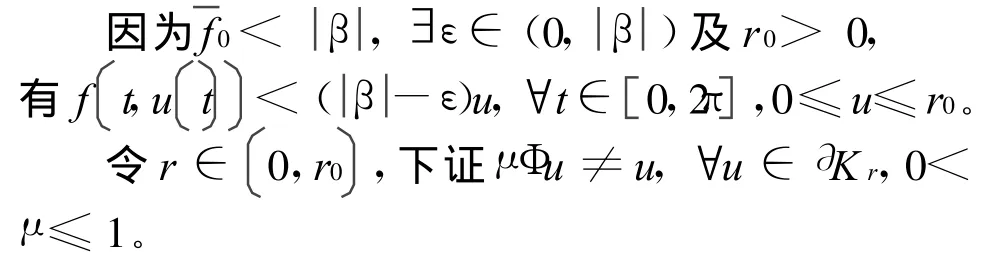
反证法:若 ∃u0∈ ∂Kr,0＜μ0≤1,使

由算子 Φ定义知,u0(t)满足下式

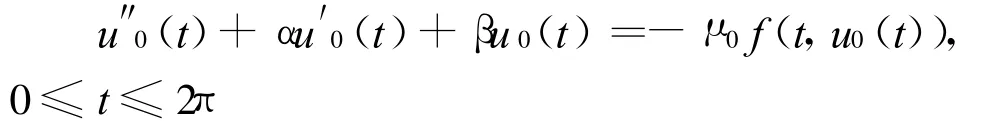
由上式及边值条件,可得

由引理5,有

另一方面:

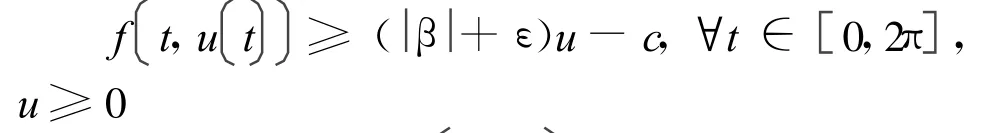
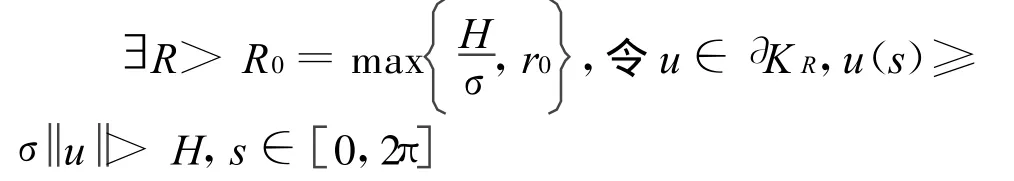
可得:

由引理6(1)知成立下式。

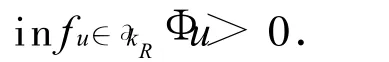
再利用反证法 ∃u0∈ ∂KR,μ0≥1使 μ0Φ u0=u0,可得:

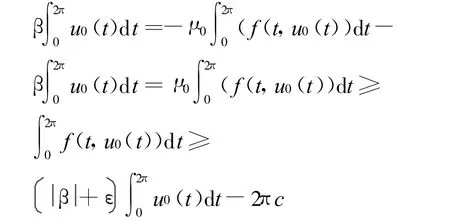
由K⊂E的定义知

综上,则有

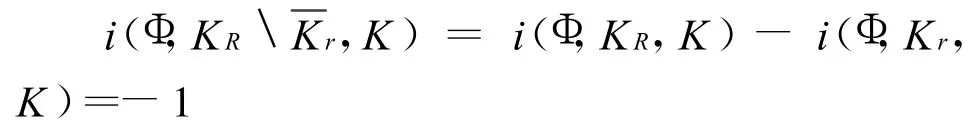
证毕。

3 结语

本文研究了一类二阶非线性周期边值问题在双参数在某种取值范围下,构造给出了该问题的两种形式Green函数,通过Green函数的性质,进而将该边值问题转化为等价的积分方程,在适当的空间上定义映射,再将积分方程转化为算子方程,利用锥不动点指数定理,给出了此问题存在正解的充分条件,并证明了正解的存在性。

[1]张玲忠.二阶微分方程周期边值问题的反序上下解方法[J].甘肃农业大学学报,2003,38(9):304-307.

[2]李相锋.Banach空间中二阶非线性常微分方程周期边值问题[J].应用泛函分析学报,2008,10(1):92-96.

[3]伊继金.Banach空间中二阶周期边值问题的解[J].工程数学学报,2006,23(6):1105-1108.

[4]吕辉.一类周期边值问题正解的存在性[J].淮南师范学院学报,2007,9(5):4-5.

[5]金花,曹德欣.半线性二阶微分方程周期边值问题[J].南京大学学报,2007,24(1):168-176.

[6]刘喆.Banach空间二阶周期边值问题的可解性[J].西北师范大学学报:自然科学版,2008,44(2):14-25.

[7]Cabada A.The method of lower and upper solutions for second,third,fourth and higher order boundary value problems[J].Math Anal Appl,1994,185:302-320.

[8]Yongxiang Li.Positive solutions of fourth-order periodic boundary value problems[J].Nonlinear Analysis,2003,54:1069-1078.