基于智能全站仪精密三角高程测量方法研究
张 江 马文静
(中铁工程设计咨询集团有限公司,北京 100055)
1 概述
《高速铁路工程测量规范》(TB10601—2009)和《铁路工程测量规范》(TB10101—2009)要求250 km/h及以上的铁路和长大隧道、桥梁的高程控制网要达到二等以上水准测量的精度。
传统的方法是使用满足规范要求的精密水准仪及配套水准尺进行测量。在地形平坦、交通便利的地区,传统方法操作简单、精度高,而在高差变化大的山区或跨越大面积水域的区域,用传统方法测量将十分困难,且劳动强度大、效率低、测量时间长。因此,研究基于智能全站仪的精密三角高程测量方法代替二等水准测量,以弥补传统水准测量的不足,提高作业效率和降低劳动强度,具有重要的意义。
2 基于智能全站仪精密三角高程测量方法的原理
2.1 间接量取棱镜高的新方法
众所周知,传统方法进行三角高程测量需要量取仪器高和棱镜高,量取的精度在1~2 mm,不能满足精密三角高程测量的精度要求。为实现精密三角高程测量替代二等水准测量,提出了一种高精度量取棱镜高的新方法。利用特制的棱镜基座,采用全站仪间接量取置于水准点或转点上方的棱镜高度,快速方便且精度可达到亚毫米级。下面介绍该方法的测量原理。
测量中使用具有自动目标识别功能的智能全站仪1台(标称精度0.5″和1 mm+1×10-6D),精密基座1个,精密棱镜2个,三角架2个,特制量取棱镜高基座1个,观测手簿或PDA(个人数字助理)1个。
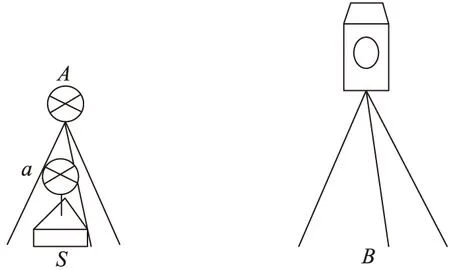
图1 间接量取棱镜高新方法示意
如图1所示,A为置于水准已知点S上方三角架上的棱镜,a为置于水准已知点S上的特制基座上的棱镜,其棱镜高HSa(棱镜点a到水准点S的高度)已知,在自由测站点B处架设全站仪,距离为20~40 m,分别测量棱镜点A和a,得到仪器中心至棱镜点A和a相应的竖直角、斜距观测值。
根据三角高程测量原理,A、B两点之间的高差计算公式如下
hAB=Ssinα+i-v
(1)
式中S——斜距;
α——竖直角;
i——仪器高;
v——棱镜高。
可得B、A和B、a之间的高差分别为
hBA=SBAsinαBA+iB
(2)
hBa=SBasinαBa+iB
(3)
由式(2)-式(3),得棱镜点a与A之间的高差haA为
haA=hBA-hBa=(SBAsinαBA+iB)-
(SBasinαBa+iB)=SBAsinαBA-SBasinαBa
(4)
特制基座上的棱镜高HSa已知,可得棱镜点A至水准点S的高差hSA为
hSA=HSa+haA=HSa+SBAsinαBA-SBasinαBa
(5)
对式(5)全微分并运用协方差传播定律,可得到高差hSA测量的中误差为
(6)
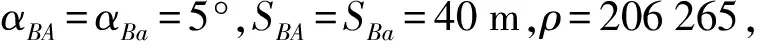
即测量仪器高的精度可达到0.19 mm,当采用多测回观测时,能获得更高的精度。
2.2 精密三角高程测量原理
首先在起始水准点上,利用间接量取棱镜高的新方法,测量得到棱镜点A与水准点S的高差hSA,将水准点S的高程传递到棱镜点A,如图2所示。
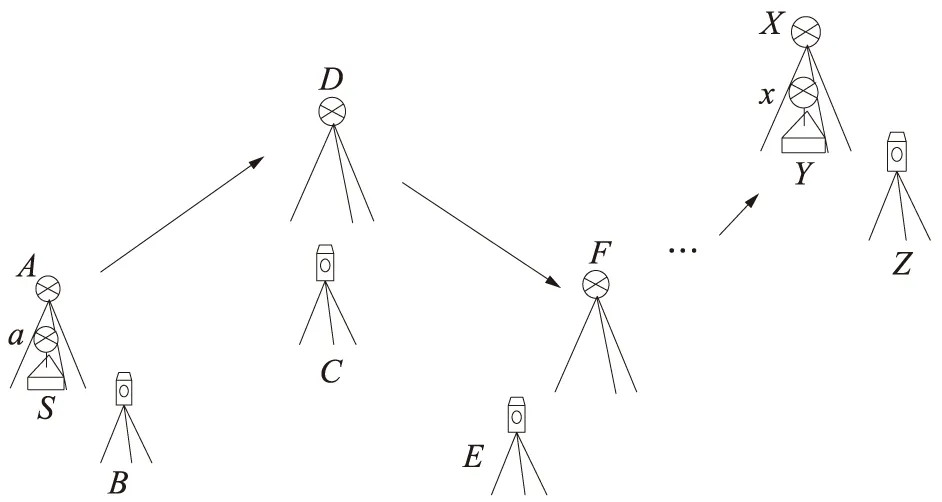
图2 精密三角高程测量方法对向观测示意
然后利用三角高程测量软件控制全站仪,在测站点B、C分别观测棱镜点A、D,测量时两台仪器同时对向观测,即先测量近距离棱镜,再测量远距离棱镜;测站点B与棱镜点A,测站点C与棱镜点D的距离一般为20~40 m,要求尽量等高。按照线路前进方向,依次按上述方法进行测量;附合到线路结束水准点时,如图2中水准点Y,为了避免量取特制基座上的棱镜高的误差,使用在起始水准点S上使用的相同特制基座来消除。在不能一次测量完成时,可以在线路走向中选择一个稳定可靠的点作为临时水准点,使用测量棱镜高新方法将高程传递到该点上,下次测量时从该点接着开始测量。
经过试验研究,精密三角高程测量过程中前后视置镜点D、F的位置可根据测量环境灵活选取,最大距离不应超过1 000 m,竖直角不宜过10°,最大不应超过15°,外业观测的主要技术要求如表1所示。

表1 精密光电测距三角高程测量观测的主要技术要求
注:S为视线长度,单位为km。
在测站B观测棱镜点A、D时,可得B至A、D的高差
(7)
(8)
其中:D为测站至观测点的平距。
测站B观测A时,因其距离为20~40 m,且大致等高,球气差可忽略不计。由测站B观测A、D之间的高差相减,得A、D之间的高差
(9)
同理,由测站C观测A、D之间的高差相减,得A、D之间的高差
(10)
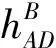
SCDsinαCD-SCAsinαCA)
(11)
按线路前进方向,将仪器B和棱镜A依次搬至E和F,重复上述的观测步骤,得D、F之间的高差hDF,接下来依次将后视的全站仪和棱镜搬至下一站的前视位置,传递高差至另一已知水准点上,在结束水准点上需利用测量棱镜高新方法,将水准点上方的棱镜高程传递到结束水准点上。
3 工程实例验证
3.1 实验地点
为验证精密三角高程测量方法的可行性和精度,本次实验地点选择在发鸠山隧道。该隧道是总长千余公里的山西中南部铁路通道的长大隧道之一,设计为单洞双线隧道,起止里程为D2K440+342~D4K454+910,全长14 568 m,进口路肩设计高程1 044.80 m,出口路肩设计高程1 084.46 m,平均路肩设计高程1 069.20 m。为了提高施工进度,发鸠山隧道设计了4座斜井,需将各洞口的高程子网布设成一个整体的二等水准网。测区范围内沟壑纵横,各水准点间联测难度大,需绕行进行水准测量,增加了外业工作量,测量周期长、效率低。
用精密电子水准仪配套铟瓦水准尺进行了整个测区的二等水准测量后,又采用精密三角高程测量方法对其中高差变化大的测段进行了验证测量。
3.2 仪器设备及人员配置
测量中使用具有自动目标识别功能的智能全站仪2台,精密基座2个,精密棱镜4个,三角架4个,特制量取棱镜高基座2个,测量手簿或PDA(个人数字助理)2个,温度计、气压计各2个,对讲机2个,测量人员6名。
3.3 外业数据采集
选取在线路走向中通视条件好、易于到达、距离适中的地方作为转点。本次外业数据采集一共联测6个水准点,从位于发鸠山隧道进口和1号斜井之间的水准点BM9042开始,联测至3号斜井处水准点BM9057结束,中途依次联测1号斜井处水准点BM9045,1号斜井与2号斜井间的水准点BM9046,2号斜井处水准点BM9051,2号斜井与3号斜井间的水准点BM9053;其中,BM9042到BM9046段进行了两次精密三角高程测量。各水准点实际分布如图3所示。

图3 发鸠山隧道精密三角高程测量过程示意
外业测量时,需根据测量距离按表1中的要求,设置精密三角高程采集软件中相应的限差:输入测回数、指标差较差、测回间竖直角较差、测回间距离较差、测回间高差较差等限差值,以便控制外业数据采集质量。
在起点BM9042处,采用间接量取仪器高的新方法,得到该点与上方棱镜的高差,在前、后视相连接的采集软件中都输入该高差值,将水准点BM9042的高程传递至其上方的棱镜,再传至前视的棱镜。在选择中间转点时,除了前后通视外,还需选在坚硬稳定的地方。在对向观测中,可通过对讲机实现同步测量,保证前、后视测量环境的一致性。
3.4 内业数据计算
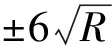
从表2可看出,五段精密三角高程测量高差值与水准测量高差值之差,都小于限差值,满足规范的要求。精密三角高程测量的总路线长度为18.74 km,水准测量的总路线长度为54.35 km,水准测量的路线长
度约为精密三角高程测量的3倍。由此可见,精密三角高程测量方法能够达到二等水准测量精度要求,且测量的效率较普通二等水准测量高。
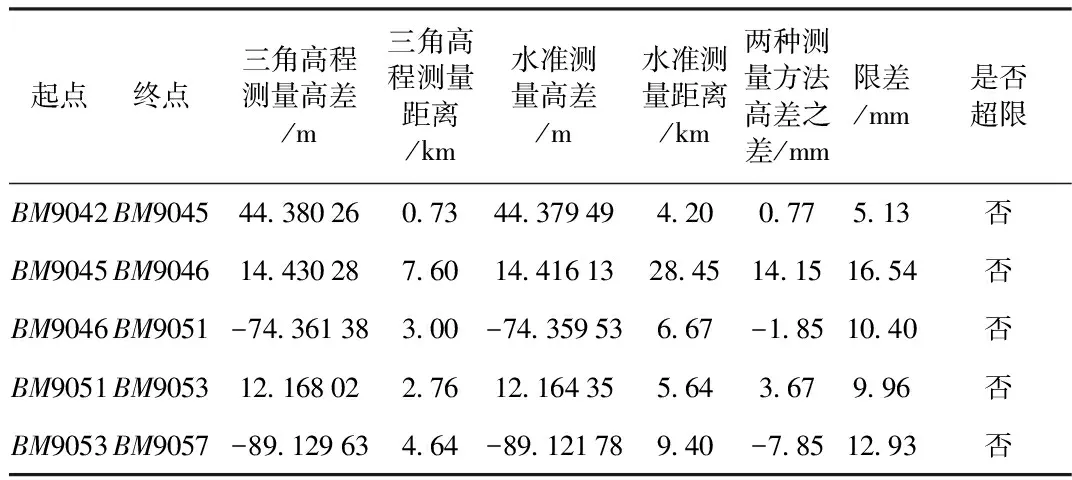
表2 精密三角高程测量与水准测量高差对比
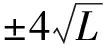

表3 往返两次精密三角高程测量结果比较
从表3可以看出,往返分别进行的两次精密三角高程测量的路线大致相同,往返测高差之差值为5.37 mm,满足二等水准测量相应的限差要求。
4 结束语
通过对比发鸠山隧道二等高程控制测量的结果,不仅验证了精密三角高程测量方法的精度能够满足二等水准测量的要求,也验证了该方法的正确性和可行性,大大提高了测量效率。结合精密三角高程测量数据采集软件和数据处理软件,为复杂山区和跨越大面积水域的二等高程控制测量提供了一种全新和高效的测量方法,该方法完全可以替代传统使用精密水准仪及其配套水准尺进行的二等水准测量。
[1]中华人民共和国铁道部.TB 10601—2009 高速铁路工程测量规范[S].北京:中国铁道出版社,2010
[2]中华人民共和国铁道部.TB 10101—2009 铁路工程测量规范[S].北京:中国铁道出版社,2010
[3]中国国家标准化管理委员会.GB/T 12897—2006 国家一、二等水准测量规范[S].北京:中国标准出版社,2008
[4]中国国家标准化管理委员会.GB/T 15314—94 精密工程测量规范[S].北京:中国标准出版社,1995
[5]中国有色金属工业协会.GB 50026—2007 工程测量规范[S].北京:中国计划出版社,2008
[6]华锡生,黄 腾.精密工程测量技术及应用[M].南京:河海大学出版社,2010
[7]李青岳,陈永奇.工程测量学[M].北京: 测绘出版社,1997
[8]赵吉先.精密工程测量[M].北京:科学技术出版社,2010
[9]梁振英.精密水准测量的理论和实践[M].北京:测绘出版社,2004
[10] 张坤宜.交通土木工程测量[M].北京:人民交通出版社,1999

