模糊决策在铁路工程地基处理方案选择中的应用

胡朝阳

(铁道第三勘察设计院集团有限公司,天津 300251)

1 软基处理方法探讨

每一种地基处理方法各有其适用范围、局限性。多数地基经过处理效果较好,达到使用要求；但也有的地基处理效果不好,这主要是地基处理方案选择存在问题,如有的地基软土层较深,采用置换方法,土方量较大,危及邻近建筑,且过深土层夯填,质量难以保证；有的软弱土层埋深较浅,可采用灰砂桩的而却采用了振冲碎石桩,虽地基承载力提高较多,但造价也增加较多；遇软弱土层较深可用碎石桩的,却采用了混凝土灌注桩等。每一种地基处理方法各有其适用条件和适用范围,不可滥用，否则技术上不合理,达不到预期效果,同时也浪费资源。在这些方案选择中,有很多影响因素,如工程造价、工期等，这些影响因素有些可以定量分析,有些具有模糊性质,只能定性分析，这些因素之间相互关联,相互制约,构成了复杂系统。模糊决策理论和层次分析法是系统工程理论中对非定量问题分析的有效决策方法，本文将构建多层次模糊决策模型,对邯黄线软基处理方案进行多因素综合分析,筛选出最优处理方案。

2 多层次模糊决策模型

2.1 建立评价模型

(1)假设采用n个因素代表某一事物,则由该因素组成的因素集合为：U={u1,u2,…,un},ui表示被考查的因素,i={1,2,…,n}。

(2)又设对某因素可能出现的评语有m个,构成评语集合为：V={v1,v2,…,vm},表示被考查因素的评判结果,j={1,2,…,m}。

(3)从集合U到V的一个Fuzzy映射Ri叫单因素评判,给出Fuzzy映射,f：U→f(v)；f(ui)=(ri1,ri2,…,rim)∈f(v)；

其中,f(ui)是关于因素ui的评语Fuzzy向量,rij表示关于因素ui具有评语vj的程度。

(4)将Fuzzy映射的全体向量合并起来得到一个关系矩阵,即综合评判的矩阵

R=(rij)m*n,i=1,2,…,n；j=1,2,…,m。

判断矩阵标度及其含义如表1。

2.2 确定因素集合U上的权重分配

层次总排序计算是基于层次单排序的结果计算指标层中的各个指标在地基处理方案中所占的综合权重,这一过程是从最高层次到最低层次逐渐进行计算的。综合权重的向量记为[WD1,WD2,…,WDn]T。

表1 矩阵标度及其含义

2.3 指标的评分标准及处理

在评价体系中,既有定性指标,又有定量指标,因此必须对所有指标的评分标准进行处理,这样才可以使评价结果具有可比性。利用层次分析法计算评价指标的权数分配可较大幅度地减少主观因素。如果人的主观判断偏离了客观实际,则CR值便显示了这种差别,以便对判断矩阵做出调整。

(1)对于定性指标,如可采用层次分析法中定性指标定量化的1～9比率标度方法评分,指标的取值范围1～9。

(2)对于定量指标,如果规范中要求指标小于或大于某值,那么根据规范要求,由专家或同行给予打分,以十分制打分,可以打零分。如果规范中没有定量要求,那么,也由专家或同行根据判断给予打分。

(3)由区域范围内岩土专家根据以上方法，对拟建工程地基处理方案进行逐项评分,取其平均值,然后进行统计。

2.4 方案比较优化

最后根据每个方案得分的多少选择最佳方案,以达到地基处理方案的优化目的。

3 实例研究

3.1 工程概况

邯郸至黄骅港铁路西起河北省邯郸市,经邢台、南宫、衡水、沧州等市至黄骅港,其中邯郸至邢台利用该段既有京广铁路,邢台至黄骅港为新建铁路，邯郸至黄骅港港区正线全长约367.6 km。

邯黄线某段软土路基位于沧州市黄骅港既有朔黄铁路北侧,全长2 260 m。经地质调查、钻探、触探揭示,本段勘探范围内地层为第四系全新统人工堆积层(Q4ml),第四系全新统冲积层(Q4al),第四系全新统海相沉积层(Q4m),局部表层夹少量植物根系,其地层自上而下分别为：素填土、淤泥、黏土、淤泥质黏土、淤泥质粉质黏土、粉砂等。其中的淤泥、淤泥质黏土、淤泥质粉质黏土的厚度最大可达6～10 m,呈流塑和软塑状态,含水量高、孔隙比大、强度很低,必须经过处理才能修筑路基。业主单位对工期、造价、环境影响提出了较高的要求,成为决策需重点考虑的因素。

采用上述多层次模糊决策模型,对袋装砂井、碎石桩、粉喷桩三种方案进行了综合评价,选出了最优方案。

3.2 加固方案层次结构模型

为进行方案对比,构造的层次递阶结构模型如图1。

目标 准则层 指标层 方案层

图1软土路基处理方案选择分层结构

3.3 影响因素权重赋值

准则层的判断矩阵见表2,指标层的判断矩阵见表3～表5。表中数据是通过对过去类似铁路工程资料的分析、计算、专家咨询和参考业主意见后确定的。

表2 准则层的判断矩阵

表3 准则层的判断矩阵

表4 准则层的判断矩阵

表5 准则层的判断矩阵

根据上面的理论,对以上矩阵进行计算，得到各自的解及一致性检验结果。

对表2,有

Wu=[0.394,0.516,0.090],λmax=3.018,

CI=0.009,RI=0.58,CR=0；

对表3～表5,有

WA=[0.75,0.25]；

WB=[0.070,0.255,0.080,0.595]；

λmax=0.405 7,CI=0.019,RI=0.89,CR=0.021；

WC=[0.75,0.25]；

以上的解W即为某一层相对应因素对于上一层某因素相对重要性的排序权值。

3.4 方案层个体评判的指标

(1)定量指标

工程费用：参考初步设计及施工图设计的资料以价格相对比值来分析。袋装砂井、碎石桩、粉喷桩比价为30∶100∶80。则各方案的指标取值为

U1(A1)=(100-30)/(100-30)=1

U2(A1)=(100-100)/(100-30)=0

U3(A1)=(100-80)/(100-30)=0.286

工期：以时间天为计算单位。袋装砂井170 d,碎石桩为85 d,粉喷桩为75 d。各方案的指标取值为

U1(B4)=(170-170)/(170-75)=0

U2(B4)=(170-85)/(170-75)=0.895

U3(B4)=(170-75)/(170-75)=1

(2)定性指标

定性指标：维修工作量、施工技术的可靠性、处理效果、施工难易程度、环境影响及资源消耗的取值采用专家评分法,如表6所示。

表6 定性指标专家评分法

根据以上标准,派遣专业技术人员进行调查,结果平均值见表7。

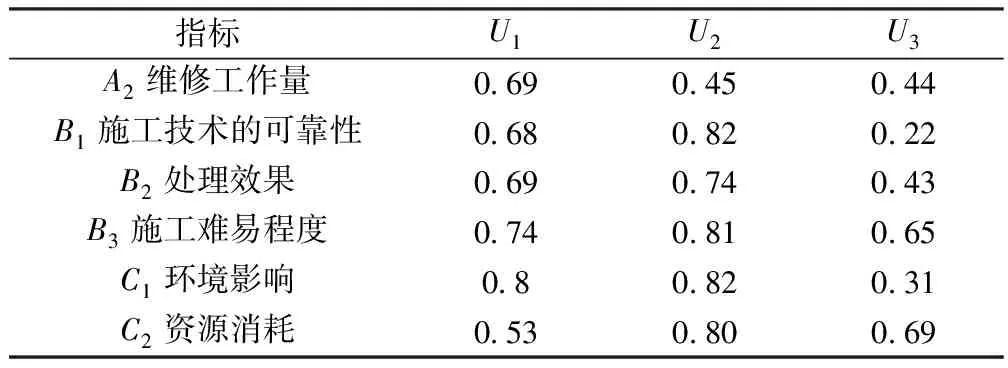
表7 定性指标评分结果

3.5 方案的综合排序

(1)方案的单排序

有了上述方案层个体评判指标的取值,就可形成方案层个体评判指标矩阵

则各方案对准则层的排序计算为

UA=WA·uA=(0.923,0.113,0.325)

UB=WB·uB=(0.283,0.843,0.772)

UC=WC·uC=(0.733,0.815,0.405)

(2)各个方案的综合排序

可见,袋装砂井软基处理方案为最优。实际施工中采用的地基处理方案为袋装砂井软基处理方案,与分析结果一致。

4 结束语

用本文建立的铁路软基处理方案的多层次模糊决策模型,对邯黄线某段软基处理工程进行了实例研究,对受到多种因素(包括定性和定量因素)制约的方案做出一个总体的评估,再据此排序选优,选择最佳方案。实际证明，多层次模糊决策模型在分析铁路软基处理方案中是可行的。

在以上计算分析中可以看出：最后的评价结果取决于各判断影响元素的取值,这些数据的获取方法至关重要，一般可以通过对过去工程资料的分析、理论计算和专家咨询等方法。在确定影响因素权重值时,误差会随着影响指标的增多而增大,应考虑对方案影响较大的指标进行评估。

多层次模糊决策模型不仅适用于软土地基加固设计的方案选择,而且还可以将其扩展到其他方面的工程项目中去,诸如铁路选线、工程设计方案优选、工程投标决策等。

[1]林宗元.岩土工程治理手册[M].北京：中国建筑工业出版社,2005

[2]吴邦颖, 张师德等.软土地基处理[M].北京：中国铁道出版社,1995

[3]贺仲雄.模糊数学及其应用[M].天津：天津科学出版社,1984

[4]李国和,刘远峰,崔维孝.高标准铁路软土地基处理方法适宜性探讨[J].路基工程,2002,104(5)：54-60

[5]赵焕臣,许树柏,和金生.层次分析法[M].北京：科学出版社,1986

[6]龙许友,魏庆朝,赵金顺.基于神经网络和灰色系统理论的新建铁路基本走向智能决策支持系统研究[J].铁道勘察,2006(4)：12-15