似大地水准面精化方法研究与精度分析

陈达玉 谯 勇 刘 俊 李春华

(1.四川省地质测绘院,四川成都 610017； 2.成都市勘察测绘研究院,四川成都 610081)

随着GPS连续运行参考站系统(Continuous Operation Reference Stations缩写为CORS)的广泛建立与应用,网络实时动态差分(Network Real Time Kinematic,NRTK)测量模式正逐渐成为无线通讯良好地区(如城市或经济发达地区)的主要测量手段,并部分或全部取代常规RTK。

NRTK的精度测试标明,其平面定位精度优于±3 cm,大地高定位精度优于±5 cm[1,2],GPS静态定位大地高精度则可以达到±0.5 cm[2]。而GPS得到的是没有物理意义的几何高,不是我们常用的具有物理意义的正常高,需要采用似大地水准面模型进行转换。只有具备了相应级别的似大地水准面模型,才可以将GPS大地高转直接换成相应精度的正常高,以代替劳动强度大且效率低的传统水准测量,实现GPS技术在几何和物理意义上的三维定位测量,满足大比例尺地形图测绘、施工放样、市政工程、航外像控等测量项目的需要。

1 似大地水准面的精化方法

大地高与正高或正常高之间的差距,分别称为大地水准面差距N和高程异常ξ,求解N或ξ的主要方法有几何法、重力法及组合法等(以下不再严格区分N和ξ)。

大地水准面精化的几何法又称为直接法,它是根据一种几何关系直接测定两点之间的大地水准面高程差,或一点的大地水准面相对于参考椭球面的高程,主要包括天文水准、卫星测高和GPS水准[3]。天文大地法需要知道测点的天文大地垂线偏差,精度较低,我国境内似大地水准面(LQG-60)精度平均为±2.7 m,在边远地区更差。目前均采用GPS水准方法,并这种方法确定的大地水准面称为“GPS大地水准面”。

GPS水准几何法是按照一定密度(一般为5～10 km)布设GPS重合点,按照公式(1)计算各离散点的大地水准面差距N或高程异常ξ,再按照一定的内插模型生成1′×1′(约2 km)或2.5′×2.5′(约5 km)的格网几何似大地水准面。

N=H-hg或ξ=H-hγ

(1)

重力法又称为间接法,它是根据一种或多种重力数据作为边值,建立关于扰动位的相应重力(大地测量)边值问题(Stokes理论或Molodensky理论),通过求解边值问题确定扰动位函数,再由Bruns公式转换为大地水准面高程[1,4]。

组合法首先应用移去-恢复原理和1D-FFT技术计算重力大地水准面,即似大地水准面的长波分量,并将它拟合(一般采用多项式拟合)到由GPS水准确定的几何大地水准面上(即似大地水准面的短波分量),消除这两类大地水准面之间的系统偏差,使似大地水准面满足实际精度要求。该方法的关键数据包括：高精度和高分辨率的GPS水准数据和地形数据、高阶重力场模型、重力异常数据和地形数据(如DEM)。

区域大地水准面的计算模型如下[5]

N(φP,λP)=NGM(φP,λP)+NRES(φP,λP)+NT(φP,λP)

(2)

其中,NGM、NRES和NT分别为重力场模型大地水准面、残差大地水准面和DTM的间接影响,φi和λi分别为大地纬度和经度。

重力似大地水准面与GPS水准所测定的高程异常之间系统偏差的消除采用五参数模型,计算公式如下

Δξ=x0+x1cosφicosλi+x2cosφisinλi+

x3sinφi+x4sin2φi+vi

(3)

其中xi(i=0,1,2,3,4)为未知参数,vi为随机噪声。

基于格网模型的内插计算采用加权平均内插模型。

顾名思义,加权平均法是取拟合点周围若干个点的高程异常的加权平均值作为该点的高程异常值,即

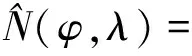
(4)

2 计算实例

下面以某地区的GPS水准数据、WDM94地球重力场模型以及该地区的重力资料等分别计算了该地区1′×1′的几何似大地水准面和重力似大地水准面,并比较两者之间的精度差异。

2.1 GPS水准数据精度

该测区介于东经104°15′～104°35′、北纬30°00′～31°25′之间,面积6 000余km2。地貌分为平原、浅丘、深丘三种类型,一般海拔在450～750 m之间,平均海拔约530 m。

共有34个GPS控制控制点,采用双频GPS接收机按照三等GPS控制网的技术要求进行施测,并以该地区的GPS连续运行参考站(Continuous Operation Reference Stations缩写为CORS)的2000坐标为起算数据,获取各GOS点的三维大地坐标B、L、H。GPS点位分布见图1。

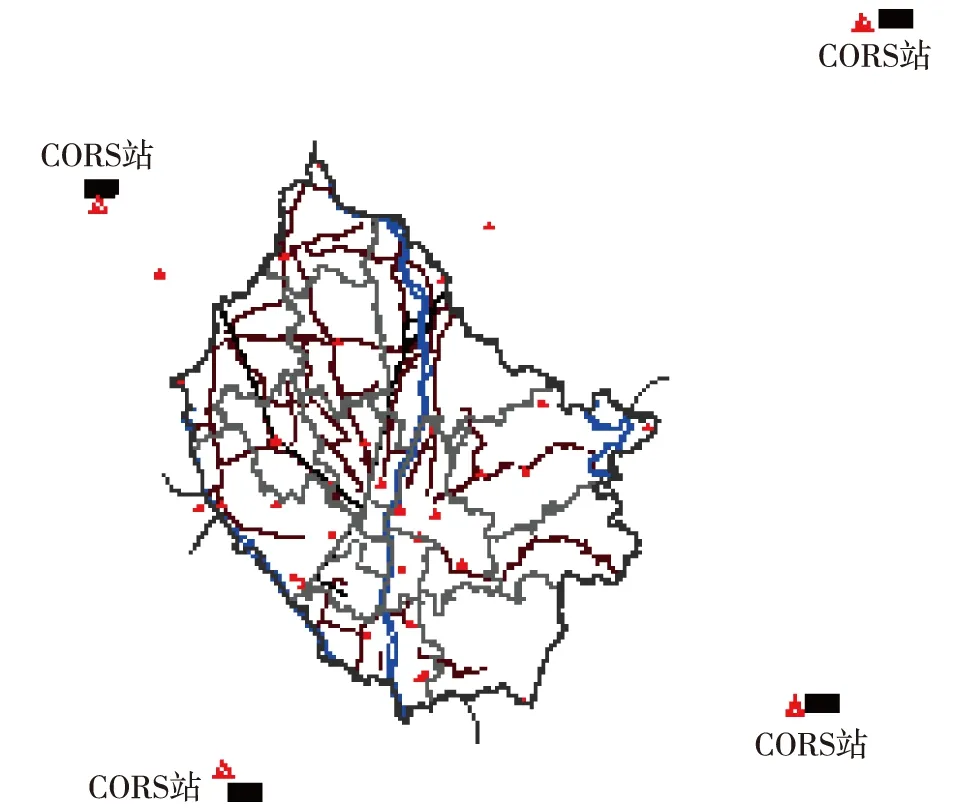
图1 GPS点位分布

以某个CORS站的2000大地坐标为起算数据进行三维无约束平差,平差后个GPS点的精度统计如下：经纬度方向的最大误差值均为0.5 cm,最小误差值均为0.1 cm,大地高最大误差值为1.4 cm,最小误差值为0.4 cm,平均误差值为0.7 cm。各GPS点的误差分布见图2。

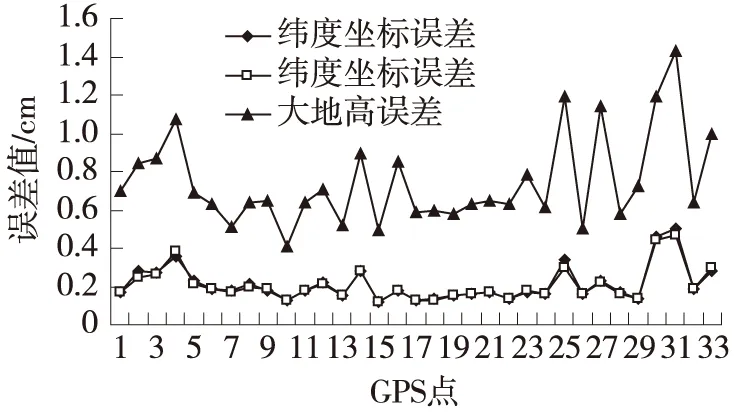
图2 各GPS点坐标分量误差分布

对三等GPS点施测了三等水准,水准网平差后的单位权中误差为±2.9 mm,约为限差(±6 mm)的1/2。

GPS水准实测数据表明,GPS水准点高程介于470～690 m之间,平均高程约为530 m,高程异常的最大值为-40.7 m、最小值为-41.8 m,高程异常起伏为1.1 m左右。

2.2 计算结果与精度分析

为了评价计算方法的可行性和有效性,从该地区的四等水准和四等GPS控制网中选取了20个分布均匀的GPS水准重合点(大地高及水准高程中误差均优于±1.0 cm)作为检核点。

以WDM94作为参考重力场模型,联合该地区的GPS水准数据、重力数据和数字地形资料,计算了该地区1′×1′(约2 km)格网重力似大地水准面模型。采用加权平均进行模型内插,与30余个GPS水准点的高程异常比较,其内符合精度(标准差)为±0.3 cm。20个检核点的精度标明,其外符合检验精度(标准差)为±2.3 cm。

同时,仅以30余个离散GPS水准点数据生成1′×1′格网几何似大地水准面模型,其内符合精度与外符合精度(标准差)分别为±0.5 cm和±2.7 cm。两种模型的精度统计见表1。

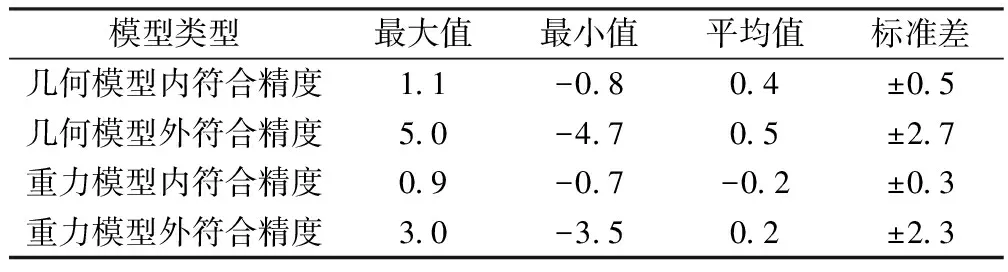
表1 高程异常的检核结果 cm

表1的结果表明,该地区的重力格网模型似大地水准面精度略优于几何格网模型,但二者之间的精度等级基本一致。

3 结论

本文的研究表明,在几千平方千米地势起伏不大的平原或丘陵地区,仅依靠GPS水准资料获得的几何似大地水准面格网模型与利用重力资料、地球重力场模型和GPS水准数据等资料确定的重力似大地水准面模型精度大致一致(后者精度略高)。同时,随着各地区,尤其是中小城市的GPS控制网和水准控制网的建立与更新,可以根据当地的测绘资料成果直接计算本地区具有厘米量级的几何似大地水准面模型,满足城市一般测绘工程高程转换,尤其是网络RTK测量实时高程转换的需要。

[1]李春华.基于网络GPS和精化大地水准面的区域实时三维定位理论与应用[D].成都：西南交通大学,2010

[2]李春华,黄丁发,罗志才,等.成都市似大地水准面的精化与应用[J].大地测量与地球动力学,2009,29(1)：83-87

[3]Yang Zhanji. Precise Determination of Local Geoid and Its Geophysical Interpretation[D]. Hong Kong: The Hong Kong Polytechnic University, 1998

[4]李建成,陈俊勇,宁津生,等.地球重力场逼近原理与中国2000似大地水准面的确定[M].武汉：武汉大学出版社,2003

[5]宁津生,罗志才,杨沾吉,等.深圳市1 km高分辨率厘米级高精度大地水准面的确定[J].测绘学报,2003,32(2)：102-107