一种复杂电磁环境下雷达信号综合分选方法*

熊永坤，时 磊，王瑞革

(92782 部队，河北 秦皇岛 066200)

1 引言

雷达脉冲信号分选是雷达对抗侦察系统的关键技术之一，是指从随机交叠的脉冲信号流中分离出各个雷达的脉冲信号并选出有用信号的过程。当前的分选算法主要基于分析截获信号的各种常规参数，例如到达时间、到达角、载频、脉宽等，其中利用到达时间的信号分选即PRI分选在预分析完成后进行，是最终的分选，也是必不可少的分选。本文将介绍累计差值直方图法(CDH，Cumulative Difference Histogram）、序列差直方图分选算法(SDH，Sequential Difference Histogram）和改进的PRI(Pulse Repetition Interval）变换算法分选，重点分析由SDH和改进的PRI 变换相结合的信号分选算法［1］。

2 雷达信号的PRI 特征

雷达信号的PRI 参数是指某部雷达相邻两个脉冲之间的时间间隔序列。一部雷达可能具有多种工作样式和工作参数，而PRI 是其中参数范围最大、工作样式最多的参数。图1分别显示了固定PRI、参差PRI、抖动PRI、参差抖动PRI 到达脉冲序列的波形［2］。

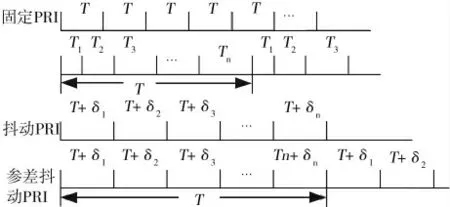
图1 典型雷达信号PRI 特征

图1中，T 是非变的固定常数，n为周期参差数，T1～Tn为n个确定性的常数，每经过n个脉冲，各PRI值循环变化一次。δn一般为在区间［－T，T］对称分布的随机序列。

3 常见PRI 估计算法

目前，估算脉冲重复间隔已提出了多种算法，主要是利用脉冲到达时间(TOA）来估算。这些算法都是以计算脉冲序列的自相关函数为基础。下面简要介绍CDH、SDH和改进的PRI 变化法这3 种算法，重点分析由SDH和改进的PRI 变换相结合的信号分选算法。

3.1 CDH算法

CDH算法基于周期性脉冲时间相关原理，对传统的直方图计算法有较大改进。它是一种基于直方图统计和序列搜索的混合算法，其基本原理是通过积累各级差值直方图来估计原始脉冲序列中可能存在的PRI，并根据该PRI来进行序列搜索。CDH算法的检测门限为

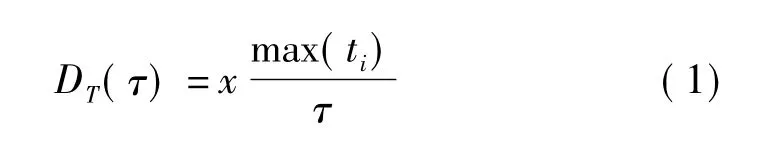
其中τ为直方图的自变量；x 可根据实际情况调节，一般取x＜1；ti为脉冲到达时间［3］。

CDH算法需要将直方图中每个PRI 间隔的直方图值以及二倍PRI 间隔的直方图值与门限比较，若两个值都超过门限，则进行搜索。这是针对二次谐波存在的情形，即存在足够数目的间隔为PRI的3个脉冲序列，而不是只存在足够数目的间隔为PRI的两个脉冲序列，而解决此问题可在序列搜索中用3 脉冲搜索的方法解决。这样做将耗费大量时间，因此提出了SDH。

3.2 SDH算法

SDH算法是一种在累计差值直方图算法基础上的改进算法，也包括PRI的建立和序列检测两部分组成，其步骤如下:

首先，计算相邻两脉冲的TOA 之差构成第一级差值直方图，并且计算检测门限，然后进行子谐波检测，若只有一个值超过检测门限，则把该值当作可能的PRI进行序列搜索；当多个辐射源同时出现时，第一级差值直方图可能会有几个超过门限的PRI 值，并且不同于实际的PRI 值。此时，不进行序列搜索，而计算下一级的差值直方图，然后对可能的PRI 进行序列搜索。若能成功地分离出相应的序列，则从采样序列中扣除，并对剩余脉冲列从第一级开始形成新的差值直方图。再经过子谐波检验，然后对超过门限的峰值进行序列搜索，最后进行参差鉴别。SDH算法的检测门限为

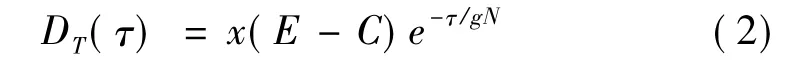
式中，E 是脉冲总数，C 是差值直方图的级数，g为小于1的正常数，N 是直方图上脉冲间隔的总刻度值，常数x 由实验确定。

3.3 改进的PRI 变换法

PRI 变换算法仅对固定重频的脉冲序列有效，当输入脉冲为抖动重频时:(1）若PRI 抖动范围大于PRI箱的宽度，则脉冲间隔会分布到真是PRI 附近的几个箱去；(2）当脉冲个数越大时，相位因子的误差也越大。显然这两点将导致PRI 变换算法不适应于PRI 抖动的脉冲。

下面来解释相位因子随着PRI 抖动时误差增大的原因。假设输入的是一列随机抖动的PRI 脉冲列，其各个脉冲的到达时间为

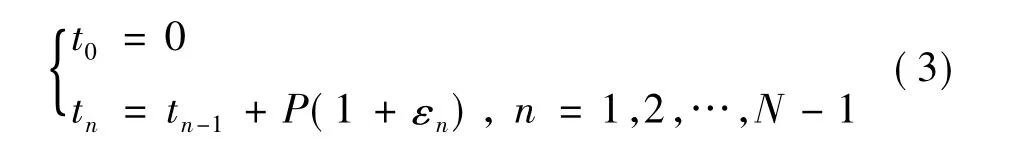
式中，p 是PRI中心值，εn是相邻脉冲间隔相对于p的变化范围。假设εn是在均值为0、方差为σ2的独立分布随机变量。在上述假设下，PRI 变换的相邻脉冲相位为

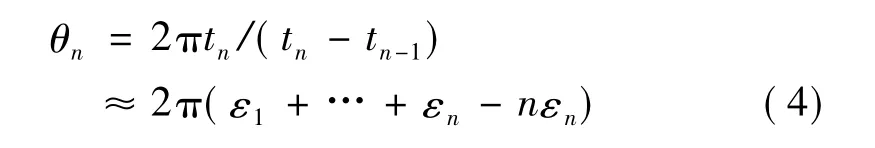
这意味着相位误差随着n的增大而增大，这样经过PRI 变换后真实的PRI 值就可能淹没在噪声中。

针对传统PRI 变换法的缺陷，一种改进的PRI 变换法被提出，即将交叠的PRI 箱与改变开始时间这两种方法结合起来。这两点改进很好地克服了传统PRI变换法的缺陷。

3.4 基于SDH算法和改进的PRI 变换相结合的信号分选

通过以上介绍，利用PRI 进行分选的算法有很多，这些算法在单独使用时都存在一定的缺陷。例如，SDH算法和CDH算法是以计算接收脉冲的自相关函数为基础，但由于周期信号的相关函数乃是周期函数，所以很容易出现信号的脉冲重复间隔及其整数倍值同时存在的现象，改进后的PRI 变换算法对于重频抖动的脉冲序列具有很好的检测效果，但是依然不适用于重频参差的脉冲序列。将这些算法组合使用、取长补短是十分必要的，基于SDH和改进的PRI 变换相结合的算法便是一例，其基本分选流程如图2。

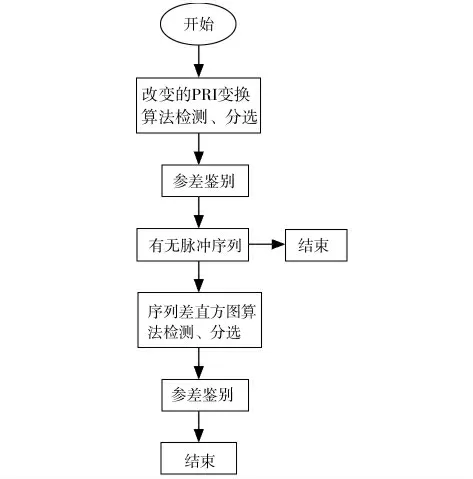
图2 综合分选流程图

雷达脉冲序列经过预分选后，首先用改进的PRI变换算法完成对固定重频脉冲序列与抖动重频脉冲序列的检测，利用检测出来的PRI 值对原始脉冲序列进行抽取。此处须注意的是:如果参差重频脉冲序列的几个子周期较为相近时，则其会被当作抖动重频脉冲序列而检测出来，因而改进后的PRI 变换算法对于抖动量在30%之内的抖动脉冲序列有效，所以对抽取出来的脉冲序列做序列直方图，通过观察其PRI 值的分布状况来进行参差鉴别。此时，再看抽取后的原始脉冲中海剩下多少脉冲，若脉冲数够多则可能存在参差重频或相同重频的几部雷达的脉冲序列，最后再利用序列差直方图算法对剩下的脉冲串进行检测、分选以及参差鉴别［4］。

4 仿真分析

假设有3 列脉冲序列:一列为固定重频脉冲序列，TPRI=420μs；一列为抖动重频脉冲序列，它的TPRI=530μs，抖动量为10%；一列为三参差重频脉冲序列，子周期分别为110、250和300 μs。首先用改进的PRI 变换算法来计算它们的PRI 值，结果如图3所示。

由图3 可以得知，有两列脉冲序列的TPRI，分别为420.7和531.1 μs，然后依次以这两个PRI 值对脉冲串进行抽取并依次进行参差鉴别，最后得知这两列脉冲序列中无重频参差脉冲序列，再对剩下的脉冲进行三阶序列差直方图算法的检测，可以得到图4。

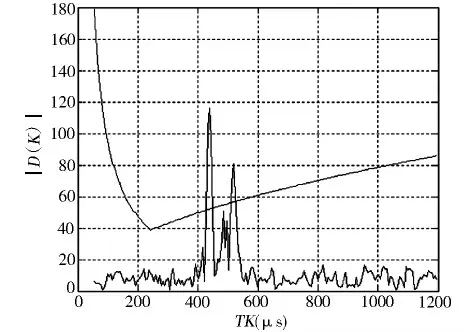
图3 改进的PRI 变换算法检测图

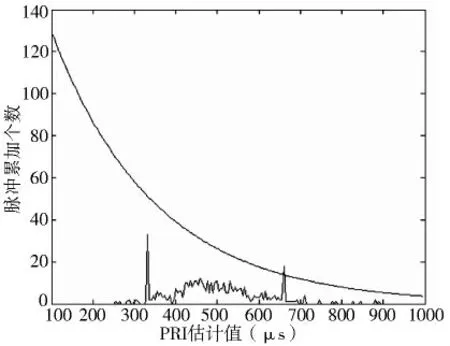
图4 三阶序列差直方图

对图4 进行综合分析并经过参差鉴别后可知，剩下的脉冲为一列三参差重频的脉冲序列，它的帧周期为660.7 μs。

以上便完成了该雷达脉冲串的分选，分选结果见表1。

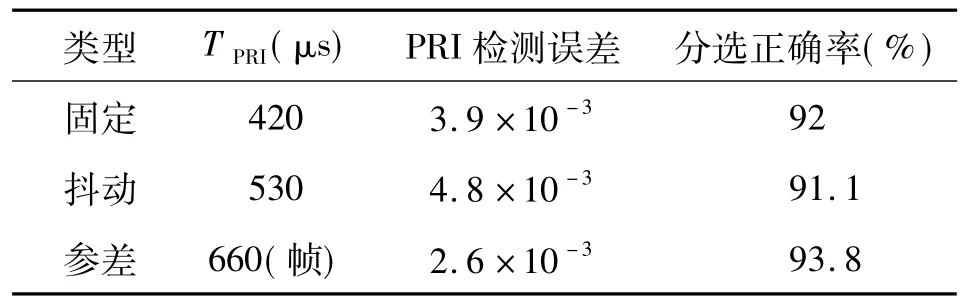
表1 分选结果

由表1 可以看出，该算法可行且分选效果好。仿真表明，SDH 法和改进的PRI 变换法的综合分选方法达到了预期效果。

5 结束语

随着雷达技术的迅猛发展，雷达参数复杂多变，重频样式更是丰富多变。基于SDH算法和改进的PRI变换相结合的信号分选技术将在雷达对抗侦察系统中获得广泛应用。

［1］周一宇.电子对抗原理［M］.北京:电子工业出版社，2009.

［2］曾志伟.雷达情报侦察系统信号分析和识别［D］.成都:电子科技大学出版社，2006.

［3］何炜.雷达信号分选关键算法研究［D］.电子科技大学，2007.

［4］袁学华，俞红兵.雷达信号识别技术研究［J］.电子工程，2003(1）:1-6.