基于模糊层次分析法的产品特性分类模型

李鹏举，程中华，李欣玥

（军械工程学院 装备指挥与管理系，石家庄 050003）

0 引言

产品特性分类工作由设计部门负责，是指在特性分析（技术指标分析、设计分析和选定检验单元）的基础上确定配套产品的关键件、重要件和一般件[1]。其目的是将设计人员对重点产品控制意图传递给工艺、制造、采购和检验部门，以便在各环节中采取重点预防、监督、管理的措施，保证产品质量的稳定性和可追溯性。产品特性分类是武器装备研制设计的重要环节，也是各级有关部门、合同商实行重点控制的主要依据[2]。

根据产品可能出现故障后果的严酷度等级及故障发生概率，当前产品特性分类方法主要有风险优先数（RPN，Risk Priority Number）法和危害性矩阵法。这两种方法着重考虑的是产品的安全性，而忽略了装备寿命期中的维修性、保障性因素。文章针对这些不足，在原有特性分类方法的基础上，采用系统工程中的层次分析法将定性指标和定量指标相结合考虑，满足了特性分类指标多样化的要求。同时，根据准则权重和评分结果得出的产品优劣排序，可以辅助指导设计人员按照关键件、重要件比例进行产品特性分类工作。

1 模糊层次分析法基本过程

层次分析法（AHP，Analytical Hierarchy Process）是美国运筹学教授Saaty于20世纪70年代提出了一种定性分析和定量分析相结合的系统分析法。它通过建立层次结构模型和判断矩阵的方式对层次中的元素进行排序，从而把一个复杂的决策问题简单化，为解决问题提供客观依据。为了改进AHP中诸如判断一致性与矩阵一致性的差异、一致性检验困难和缺乏科学性等问题，一些学者提出模糊层次分析法（FAHP，Fuzzy AHP）。与AHP相比，FAHP通过元素两两比较构造模糊一致性判断矩阵，更符合人的思维和心理特点，并解决了AHP存在的一些问题，因此FAHP在决策分析中得到了广泛的应用。

1.1 建立层次结构

应用层次分析法进行产品特性分析决策时，首先要建立评价问题的层次结构。层次结构是应用层次分析法把复杂问题分解简化的关键，必须在对评价原则和意图深刻分析理解的基础上进行。结构中的最上层是评估目标，中间层是准则层，最底层是评价对象（产品层）。准则层可以包含多级，同级之间相互独立，上下级之间为隶属关系[3]。

参照GJB 190—86《特性分类》相关规定，结合产品特性分类工作实际，建立产品特性分类层次结构图，如图1所示。

在进行产品特性分类过程中，首先采用关键件特性准则对系统或单机内的所有产品进行评价排序；由分析人员按照关键件比例要求确定关键件后，再应用重要件特性分类准则对剩余器件进行评价排序；最后按照比例要求确定重要件和一般件。

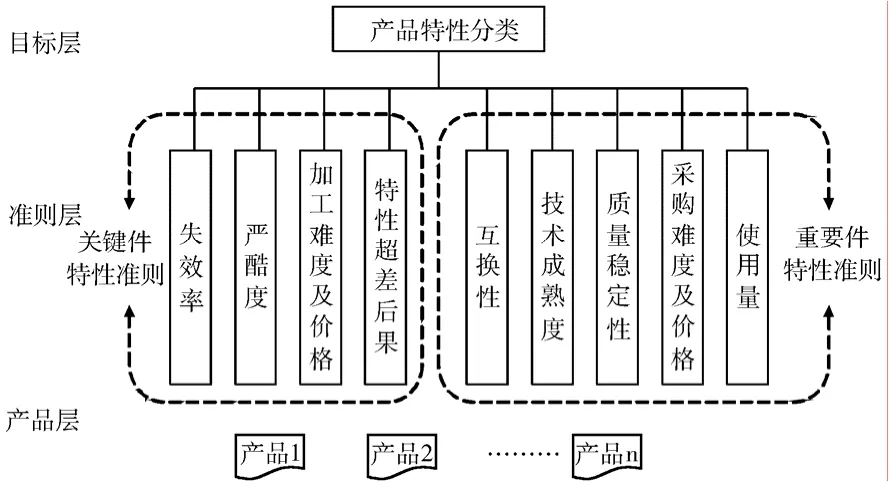
图1 产品特性分类层次结构Fig.1 Hierarchy of the classification of product characteristics

1.2 构造模糊判断矩阵

模糊判断矩阵R表示在层次结构中，针对隶属的上一级元素，某一级元素之间相对重要性的比较矩阵。例如：假定上一级元素为B1，它与下一级中的元素C1、C2、…、Cn、有隶属联系，经过专家的模糊判断，可得矩阵为

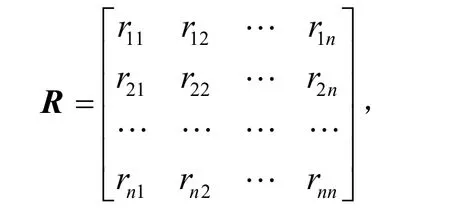
其中rij表示元素Ci相对元素Cj的重要程度的度量值，通常采用1～9标度法，如表1所示。

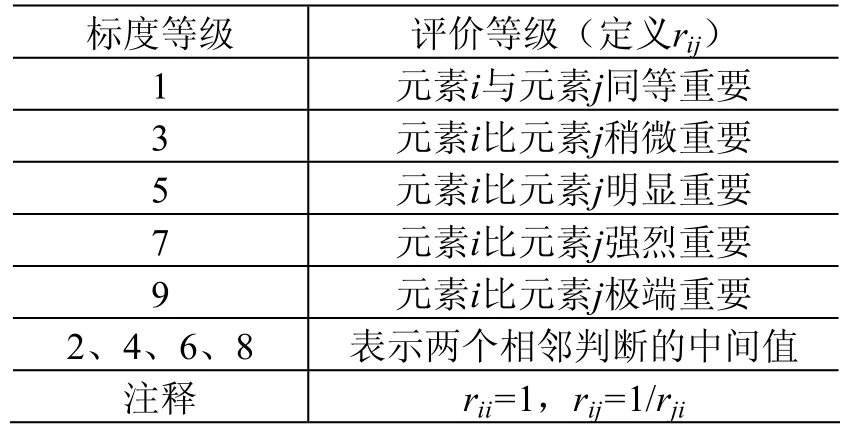
表 1 1～9标度法及其意义Table 1 Meaning of the 1～9 scaling levels

利用模糊判断矩阵计算各特性所占权重方法很多，本文选用以下公式[5]：

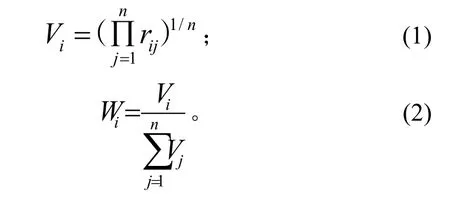
其中：V为中间变量；ij12,n=…、,,。 得出的权重向量表达式为

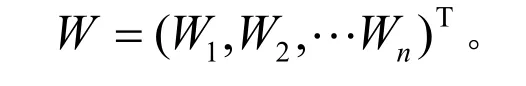
1.3 模糊判断矩阵的一致性检验

由模糊判断矩阵得到的权重值是否合理，需要进行一致性检验。模糊判断矩阵的一致性反映判断者思维的逻辑一致程度。当偏离一致性过大时，将此权重向量的计算结果作为决策依据是不可靠的[4]。

检验模糊判断矩阵一致性的公式为

其中：CR为判断矩阵的一致性比率；maxλ为模糊判断矩阵的最大特征值；n为矩阵阶数（1＞n）；RI为平均随机一致性指标，如表2所示。

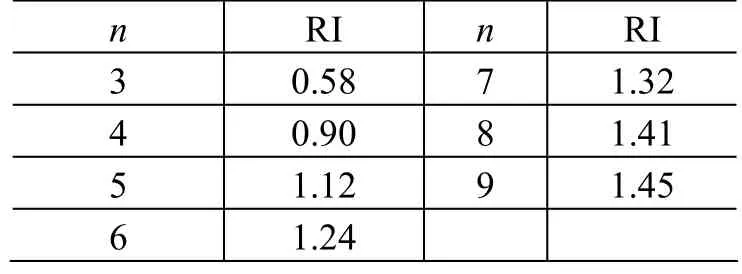
表 2 平均随机一致性指标Table 2 Mean random consistency index(RI) of 3-order through 9-order

如果 C R = CIRI＜0.1，则此模糊判断矩阵具有满意的一致性，评价结果是可靠的，否则就需要进行调整。一般对于三阶以上的判断矩阵才需要检验一致性。

1.4 确定专家权重

在对特性分类准则进行模糊评判的过程中，不同专家由于受到知识结构、评判水平和自身偏好等因素的影响，所作出的模糊判断矩阵的质量和侧重方面必然存在差异。因此，在最终确定各特性分类准则所占权重时，不能简单地将每位专家的结果相加求平均值，应有区别地对待。目前，确定专家的权重有两种方法：第一种方法是通过专家所做的模糊矩阵一致性程度来确定；另一种方法则通过不同专家所做的模糊矩阵相似程度来确定。本文选用第二种方法[5]。

设有m(m＞ 1)位专家参与人为差错影响因素的评判，第k位专家的模糊互补判断矩阵为

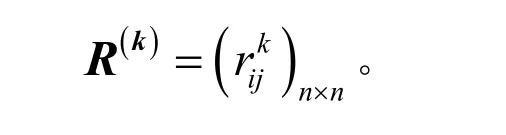
计算得第k位专家所确定的特性分类准则权重向量为

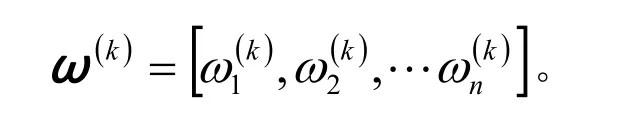
设θ表示权重向量ω(k)与ω(l)的夹角，θ的余弦

klkl定义为

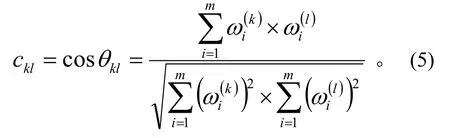
c表示权重向量ω(k)与ω(l)的相似程度，即专家

kl k与专家l判断的一致程度，c越大，表明ω(k)与

kl ω(l)越相似。

计算每个权重向量与其他权重向量的夹角余弦后，可得到矩阵

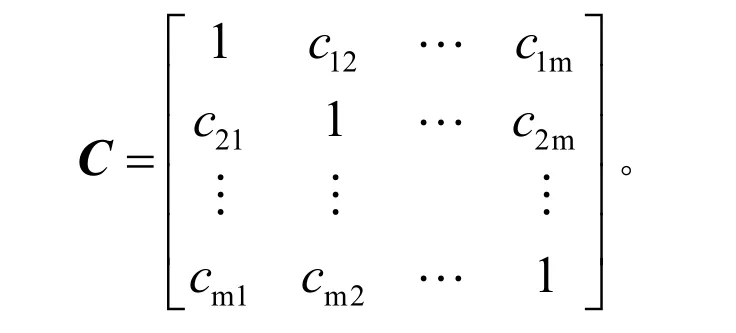
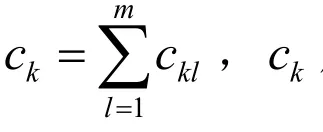
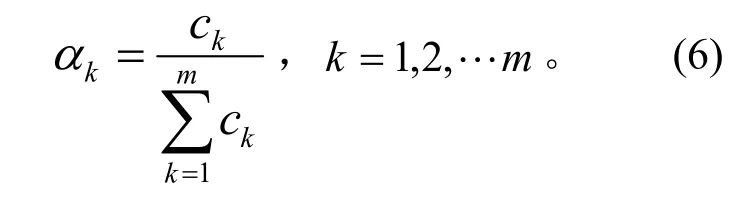
最后得出综合专家权重的特性准则权重向量为

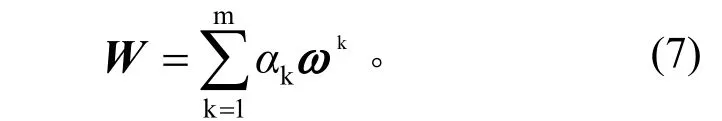
2 案例计算

现对某新型号雷达的发射机调制器组合进行产品特性分类。调制器组合是雷达发射机中的重要组成部分，其主要作用是给雷达发射机的行波管提供正负偏压、灯丝电压以及调制脉冲。

首先邀请3位不同领域的专家对关键件和重要件的特性分类准则作两两比较判断，得出互补模糊判断矩阵。第一位专家的模糊判断数据如表3所示。

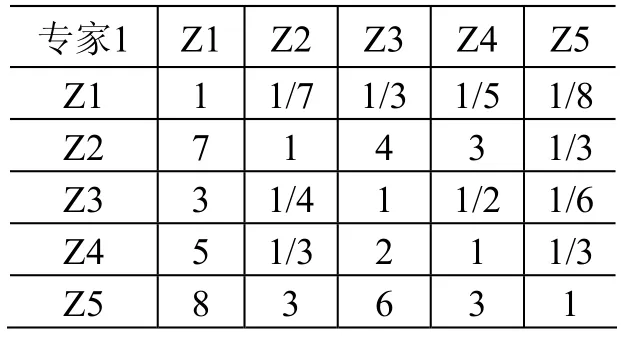
表3 专家1模糊判断数据Table 3 Fuzzy judgment data of expert A

专家1的模糊判断矩阵为

根据式(1)、(2)计算出专家1的特性准则权重向量为

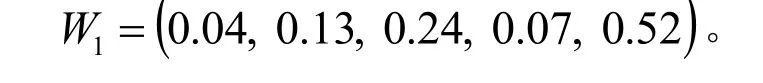
类似可得专家2和专家3的权重向量分别为

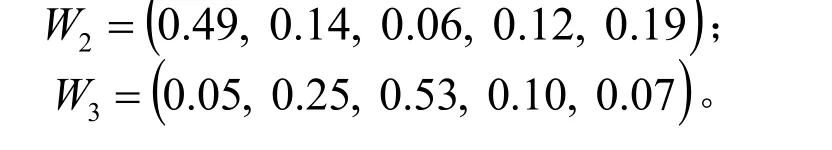
根据式(3)、(4)计算得出3位专家的模糊判断矩阵一致性指标分别为CR1=0.043 3、CR2=0.001 1、CR3=0.001 3，满足一致性指标要求。

由式(5)得到的专家权重计算矩阵C为

由式(6)得到3位专家权重分别为0.35、0.32、0.33，最终可算得重要件特性分类准则的权重为

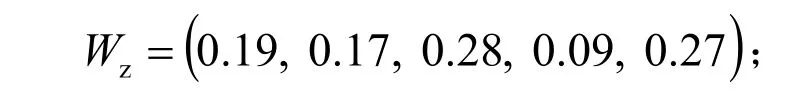
关键件特性分类准则的权重为

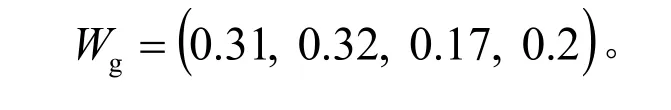
3 软件开发

笔者运用Borland Delphi 7.0和Microsoft Access 2007软件工具开发了基于模型的产品特性分类软件，界面如图2、图3所示。将专家模糊判断矩阵和器件目录导入到特性分类软件中后，分析人员对器件的各种特性按照1～10标度进行逐一打分，根据隶属度原则，加权计算后得出优劣排序，最终可以按照关键件、重要件的比例要求完成产品特性分类工作。

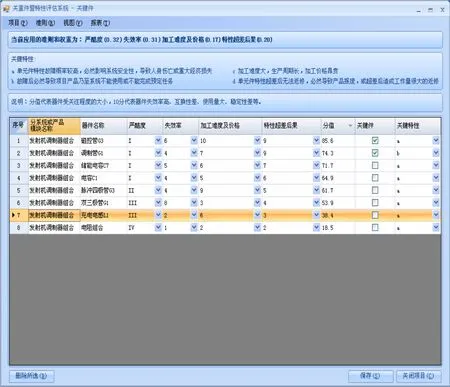
图2 关键件评价Fig.2 Assessment of key products

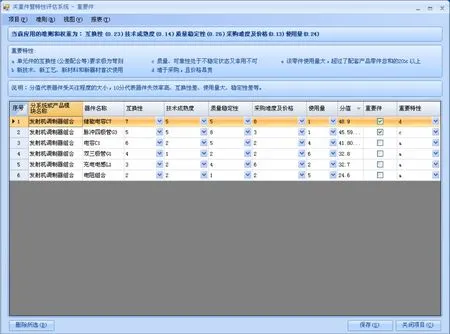
图3 重要件评价Fig.3 Assessment of important products

4 结束语

在原有的产品特性分类方法基础上建立的评价指标体系，综合考虑了安全性、维修性、保障性因素，提高了特性分类结果的客观性和可信度。FAHP能够科学确定相关特性分类准则权重，既避免了权重确定中的随意性，又考虑了主观思维判断的模糊性，是一种思路清晰、可操作性强的权重计算方法。案例分析结果表明：基于FAHP的产品特性分类方法及软件能够有效提高产品特性分类工作的科学性和效率，是对现有方法的补充和完善。

（References）

[1]陈圣斌, 周晓光.直升机可靠性关键件和重要件的确定方法及工程应用[C]//中国航空学会直升机专业分会第十九届全国直升机年会.哈尔滨： 中国航空学会,2004： 314-320

[2]李凤良.航天型号产品特性分类工作基本状况与建议[J].航天标准化, 2001(5)： 17-18

Li Fengliang.The base situation and some suggestions about classification of product’s characteristics of space product[J].Aerospace Standardization, 2001(5)： 17-18

[3]段秉乾, 司春林.基于模糊层次分析法的产品创新风险评估模型[J].同济大学学报： 自然科学版, 2008,36(7)： 1002-1005

Duan Bingqian, Si Chunlin.Comprehensive risk assessment model of complex product systems innovation based on fuzzy AHP[J].Journal of Tongji University： Natural Science, 2008, 36(7)： 1002-1005

[4]王雪青, 刘姗姗, 郭晓博.基于模糊层次分析法的代建制企业风险评价[J].北京理工大学学报： 社会科学版, 2008, 10(3)： 73-76

Wang Xueqing, Liu Shanshan, Guo Xiaobo.A risk evaluation of the agent construction company based on FAHP[J].Journal of Beijing Institute of Technology：Social Science Edition, 2008, 10(3)： 73-76

[5]刘风强, 孙志强, 谢红卫.航空维修人为差错影响因素分析中的模糊层次分析法[J].中国安全科学学报,2008,18(7)： 43-48

Liu Fengqiang, Sun Zhiqiang, Xie Hongwei.Analysis of human error influence factors in aviation maintenance based in group fuzzy analytical hierarchy process[J].China Safety Science Journal, 2008, 18(7)： 43-48