导弹遥控过程的CADET算法精度分析

花寅东，赵利强，邹士新

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

对于雷达型导弹导引头已截获目标后的导弹系统制导精度分析，CADET算法获得了广泛的应用，并有了系统的分析方法和模式。但对于导弹遥控精度这一类问题的分析，目前仍无有效的分析方法。

本文采用一个简单的二维导弹模型，仅考虑导弹的非线性误差、导弹的加速度计误差、以及机载雷达的目标探测误差，并引入CADET算法进行定量计算，从而得出各误差对遥控精度的不同影响程度，成功地对该类问题进行编程和仿真。该分析结果有助于设计者进行针对性设计和调整，提高遥控精度，进而提高导弹的制导精度，增大导弹的截获概率。

1 误差模型

遥控过程工作中的主要误差源有以下几个:载机和导弹坐标系的初始对准误差、非线性因素的误差、机载雷达的目标探测误差以及惯性器件误差。为了使仿真结果更具代表性，应该尽可能将上述误差都考虑进去，不过同时工作量也会有很大的增加。综合考虑后，假设载机和导弹坐标系初始对准很精确，惯性器件中的陀螺也没有误差，考虑导弹的非线性因素误差、导弹的加速度计误差、机载雷达的目标探测误差对遥控精度的影响。

1.1 非线性因素误差模型

遥控过程中，非线性因素也有很多，如:加速度指令限制、弹体的非线性、坐标变换、导引头天线罩像差等。在此，考虑加速度指令限制，让导弹的y向加速度经过一个限幅器，得到真实的y向加速度，可用式(1)表示:

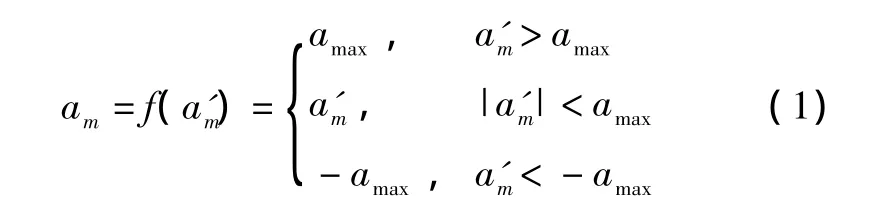
处理该非线性因素时，对该模型采用准线性化，先求其统计量:

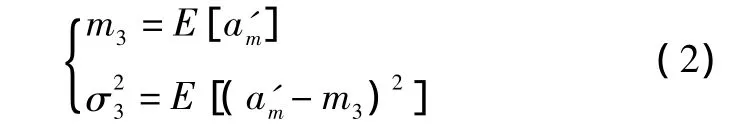
对其进行准线性化:

其中的参数可直接利用式(1)计算:

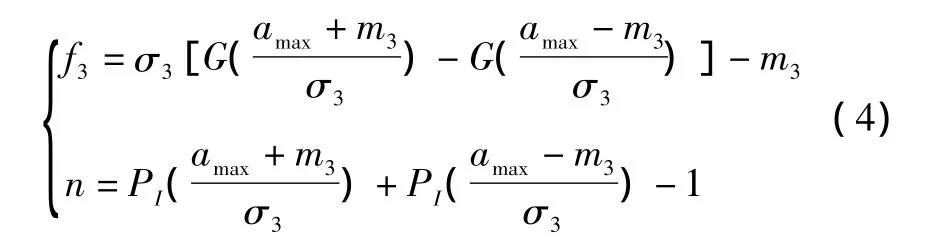
其中的函数定义如下:

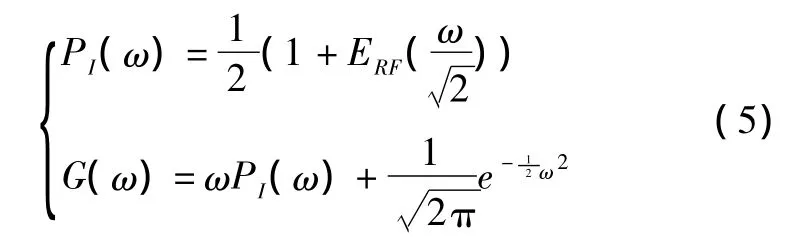
1.2 导弹加速度计误差模型

遥控过程中，导弹y向加速度由加速度计测量［2］，所得误差为

式中:ax，ay，az为导弹 x，y，z向加速度;Sy为标度因数误差;Mx，Mz为交叉耦合因数;Bf为测量零偏;Bv为振摆误差系数;ny为随机零偏。

而事实上，考虑的是加速度计的误差整体对遥控精度的影响，因此若是用上述表达式来分析，所得到的也是加速度计误差的各个分量对遥控精度的影响。所以，此处不采用该误差模型，而直接假设加速度计误差为一个高斯白噪声R(x，t)，其统计量函数可设定为均值是0，方差为一常数。即:

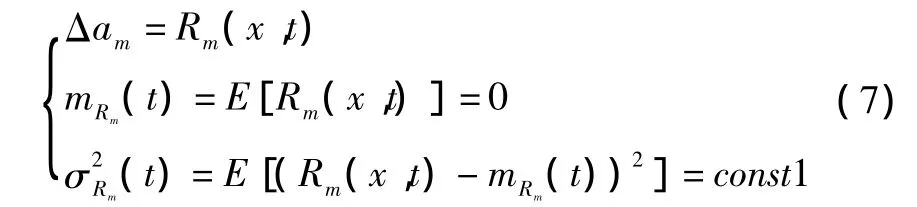
1.3 机载雷达目标探测误差模型

同样的，用机载雷达测得的目标加速度，其误差也用一个高斯白噪声表示，且与加速度计误差白噪声互不相关，其统计量函数均值也是0，方差为一常数。表达如下。

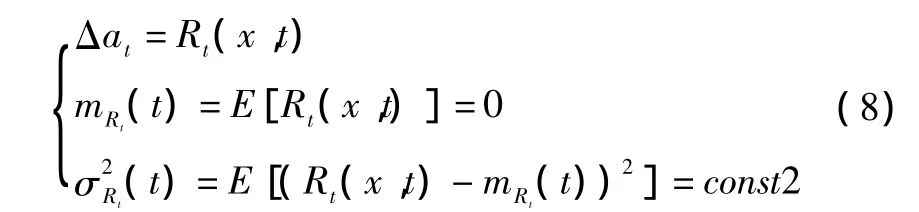
另外的，CADET算法的作用函数w(t)分解为确定性分量与随机分量之和，事实上其中的随机分量也可以认为是噪声误差项。为了研究方便，同样认为该随机分量是一个高斯白噪声，这些白噪声相互独立，互不相关。

2 系统模型

真实的系统模型需要对导弹以及目标进行力和力矩分析，分别列出运动学和动力学方程，之后求解出各个参数。不过在此，所研究的主要是导弹和目标的加速度，涉及的参数远远少于真实的系统。因此，可以直接忽略动力学方程，只需对导弹和目标进行运动学的假设，就可以推导出整个系统的方程。

导弹的遥控过程示意图见图1［1］。

图1 导弹遥控过程示意图Fig.1 The sketch map of missile’s remote control process

遥控过程需要的时间为T(即拦截时间为T)，考虑t时刻的情况，则还需要飞行的时间为tgo=T－t。导弹、目标的速度与加速度都在图1中标注，不再具体说明。

考虑y方向上的相对距离y(t)，与y方向的导弹加速度、目标加速度有如下关系:

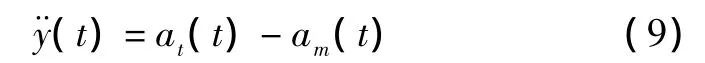
自动驾驶仪用如下线性模型的传递函数表示:

载机测得目标加速度后将数据传递给导弹，导弹采用比例导引律接近目标，加速度指令a0是与目标线角速度和径向速度之积成正比，比例系数k取为常数3，即:

则未限制的导弹y向加速度满足微分方程:

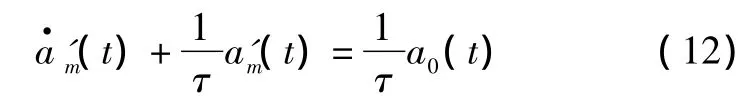
实际上，导弹的y向加速度还需要经过一个理想限幅器，模拟弹体的结构饱和效应，其表达式已在误差模型式(1)给出。

并假设目标加速度是确定性变量与有限带宽的高斯过程之和，满足:

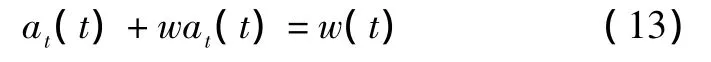
式中:w为目标机动带宽，仿真时取一常数;w(t)为随机输入。

至此，就有足够的运动学假设方程，取状态量为

由式(9)、式(12)、式(13)，经过近似、化解，可以得到状态方程如下(具体推导过程可参见参考文献［1］):

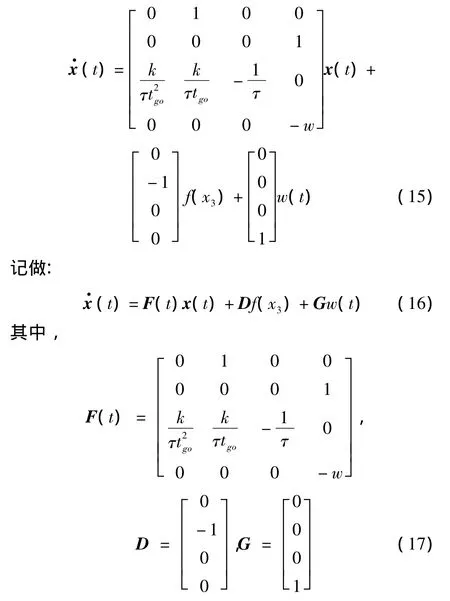
这时，再加入误差模型，实测值表达为真实值加上误差项，真实值依然满足各个假设的运动学方程。即:

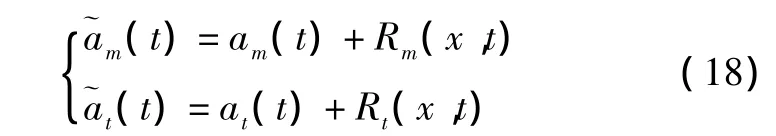
状态量取其实测值，各个运动学方程都需要做变形。如式(9)变为

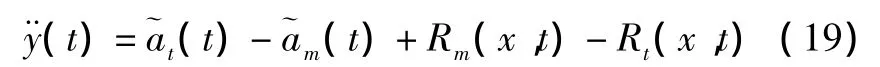
同理修正式(12)、式(13)，得到新的状态方程为

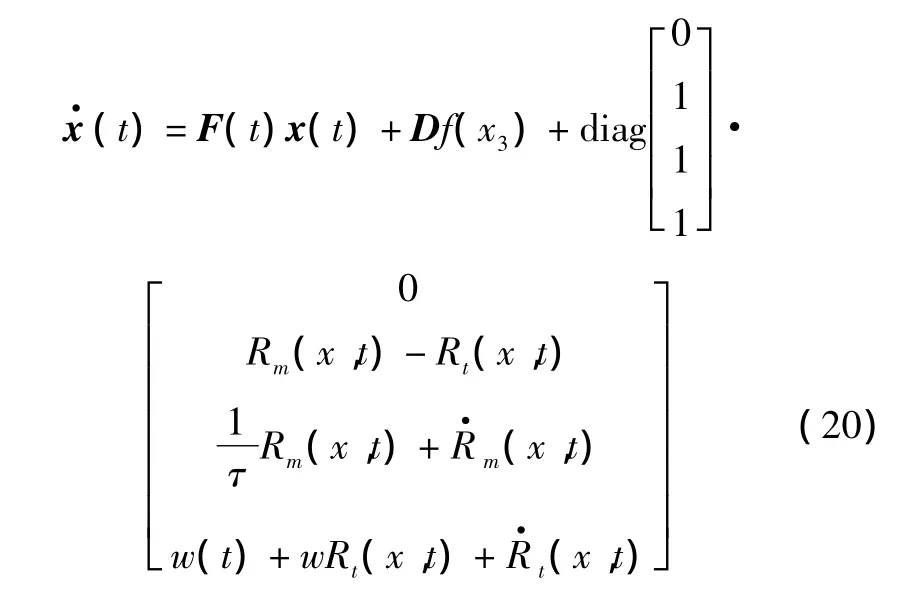
这时，状态方程的最后一项G、w(t)均发生了变化。再利用下述性质:

1)高斯随机过程的线性组合还是高斯随机过程;

2)高斯随机过程的微分(积分)还是高斯随机过程;

3)高斯随机过程的微分(积分)后得到的高斯随机过程，统计量函数是原来的统计量函数的微分(积分)。

性质1)、性质2)在介绍高斯随机过程的书籍中都有推导与证明，在这里可以简单证明一下性质3)。

考虑高斯随机过程分布函数为f(x，t)，统计量函数为均值函数m(t)，方差函数σ(t);微分后的高斯随机过程统计量函数为均值函数 m'(t)，方差函数σ'(t)。

方差函数σ(t)的推导证明复杂一些，但考虑到此时要处理的噪声函数m(t)均为常数0，则其微分也为0，此时有:

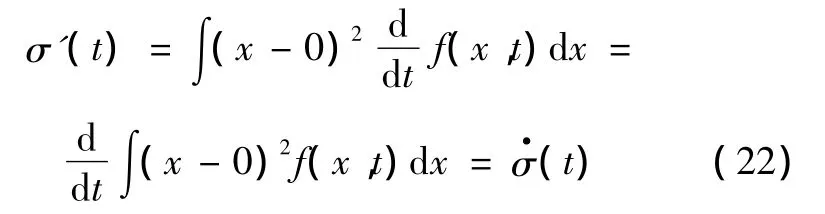
同样的，可以推导高斯随机过程积分后的统计量函数表达式。

对误差项进行化解，化成一个噪声项，令:

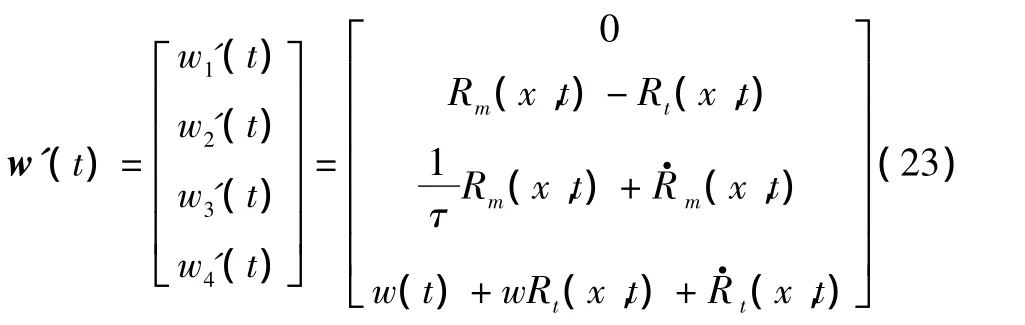
其系数为对角矩阵:

至此，可以按照定义重新计算该噪声的统计量得:

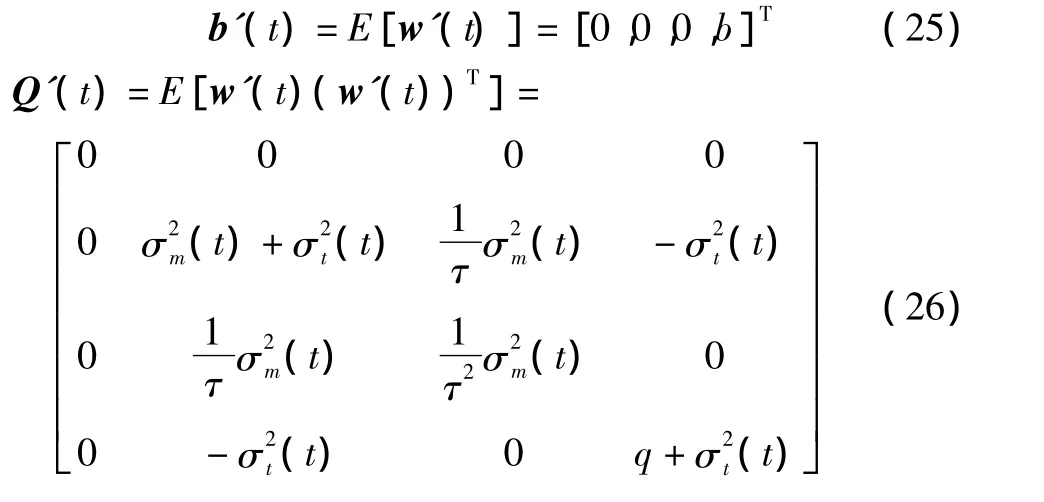
其中:参数b和q是随机输入w(t)的输入统计量，分别代表均值和方差。

将非线性项f(x3)按照式(2)～式(5)进行准线性化，并将状态方程的等式右边前两项整体作为一个非线性函数，则可以推出:

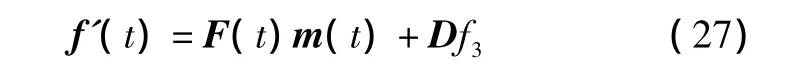
并由 N(t)的计算公式［3］得:

之后代入统计量微分传递方程［4］:

此时，就得到了统计量(包括均值向量和协方差矩阵)的微分传递方程，依次迭代、积分就能得到每一个时刻的统计量，再对此协方差矩阵进行分析，就能看出误差的影响情况了。

至此，完成了系统模型的建立。

3 仿真结果分析

上文推导的系统状态方程以及CADET算法微分传递方程，在已有条件下按照式(27)、式(28)可以得到解算，设定均值向量m与协方差矩阵P的初值为0，目标机动带宽w定为1 rad/s，时间常数τ为1 s，遥控过程的拦截时间T=10 s。

此时，有3 个误差项 amax、Rm(x，t)、Rt(x，t)会对 y向距离均方值σy产生影响，分别代表导弹非线性因素误差、导弹加速度计误差、机载雷达的目标探测误差。其中的两个噪声项由于均值统计量为0，因此主要是噪声的方差σm、σt对y向距离均方值σy造成影响，其中σy越大，表明y向距离在均值上下起伏的波动越大，误差也就越大。

当 amax=8e10、σm=2、σt=2 时，得到的误差分析曲线与无误差时CADET算法解算该模型的曲线［1］比较接近，表明该算法的可行性是可以保障的。如图2所示。

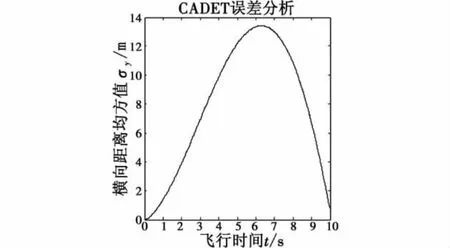
图2 amax无限制、噪声方差很小时的误差分析曲线Fig.2 Curve of error with unbounded amaxand small noise variance

但实际上，amax不可能做到无限制，往往是令其取中等限制amax=8，这时候的曲线在t=7 s之后就能明显地看出是对非线性系统进行近似的准线性系统。此时，再对σm、σt固定其中一个，令另一个的数值进行变动，得到很形象的三维曲线图，即图3。

图3 误差曲线随误差源变动的三维曲面图Fig.3 The 3D error analysis

从图3中可以看出，当导弹加速度计误差σm很小时，误差σy在达到峰值之后，又收敛回零点;但随着导弹加速度计误差σm的增大，σy－t误差曲线也一直在增大，σy峰值的幅度越来越大，取到峰值的时间也在增大，当σm增大到一定程度(约为数值8)后，取到峰值的时间在拦截时间T外，这意味着误差曲线在整个遥控过程中是一直发散的。而机载雷达的目标探测误差σt很小时，误差σy在达到峰值之后，又收敛回零点;随着σt增大，σy越来越快地取到峰值，其峰值的幅度越来越大，之后收敛速度越来越慢，以至在最后拦截时间T时，误差σy的数值还很大。

图4 增大各误差后，误差曲线的变化Fig.4 The change of error curve

此外，还可以对这3个误差源的影响程度做分析:让误差源在程序中对应的参数各自增大同一个数值(仿真时取3)，将某项参数改变后的误差曲线集中画在一个图中，就能直观地看出哪个误差源对误差的影响最大。但要注意的是，让非线性因素误差源增大，对应的是限幅器的幅值amax减小，这样对应的线性范围减小，增大了非线性因素;其他的两项误差源对应的参数都应该增大。如图4所示，可以直观地看出，导弹加速度计误差σm是对整个误差影响最大的一个误差源，在t=7.8 s之前机载雷达的目标探测误差次之，非线性因素误差最末;而t=7.8 s之后非线性误差更加明显。这与遥控过程实际工作时的误差分析是一致的。

4 结论

本文将CADET算法应用到导弹的遥控过程进行精度分析，在误差源很小的情况下得到的分析曲线与无误差时CADET算法解算该模型的曲线十分吻合，表明将该算法应用到遥控过程误差模型中是行之有效的。

量化计算误差源对精度的影响，从而判断出最大误差源是导弹加速度计误差，也和实际相符，这说明了该算法在遥控过程误差模型中的精度分析上具有独到之处。

略微不足的是本文为研究方便，并没有采用导弹六自由度的模型，而只是对相关参数做了合适的运动学方程假设;对遥控过程中“载机－导弹－目标”这三者组成的系统的工作过程也没有深入地分析。这可以作为下一步的工作，不断完善系统模型，对真实的导弹模型进行分析，从而能更精确地进行导弹遥控过程精度分析。

［1］TAYLOR J H.战术导弹制导系统直接统计分析手册［M］.赵善友，译.上海:第八二五○研究设计所，1978，12:9-13，49-50.

［2］TITTERTON D H，WESTON J L.捷联惯性导航技术［M］.张天光，王秀萍，王丽霞，译.北京:国防工业出版社，2007.

［3］PHANEUF R J.Approximate honlinear estimation ［D］.M.I.T.，Cambridge，Mass.，1968.

［4］JAZWINSKI A H.Stochastic processes and filtering theory［M］.New York:Academic Press Inc.，1970.