Effect of Hydrostatic Pressure on Input Power Flow in Submerged Ring-stiffened Cylindrical Shells
(Department of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)
Effect of Hydrostatic Pressure on Input Power Flow in Submerged Ring-stiffened Cylindrical Shells
LIU Zhi-zhong,LI Tian-yun,ZHU Xiang,ZHANG Jun-jie
(Department of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)
The input power flow for an infinite ring-stiffened cylindrical shell submerged in fluid induced by a cosine harmonic circumferential line force under conditions of a uniform external hydrostatic pressure field is investigated in this paper.The motion of the shell and the pressure field of the external fluid are described by the Flügge’s thin shell theory and the Helmholtz equation respectively.The effect of the external pressure field is modeled by including static prestress terms in the shell equations of motion.The effects of hydrostatic pressure on the input power flow are examined.The results show that the external pressure shifts the curves of input power flow to left along the frequency axis.The effect is more obvious with higher external pressure and circumferential mode.It will give some guidelines for vibration and noise control of this kind of shell.
hydrostatic pressure;input power flow;ring-stiffened shell;submerged shell
Biography:LIU Zhi-zhong(1980-),male,Ph.D.student of Huazhong University of Science and Technology,
E-mail:hichrisliu@163.com.
1 Introduction
A submerged cylindrical shell reinforced by circumferential rings is the primary structure of submarine,torpedo and all kinds of submerged vehicles.The determination of the dynamic response of the structures is thus a significant subject in vibration and noise control area.The method of vibration power flow is an effective tool used in this area,and the concept of power flow was first definitely presented by Goyder and White[1-3].Zhang and Zhang[4]have introduced the concept of power flow into the analysis of periodic shells,and studied the input vibrational power flow from a cosine harmonic circumferential line force and the power transmitted by internal forces of the shell wall in vacuo.
Fuller[5]has investigated the input mobility of an infinite elastic circular cylindrical shell filled with fluid.The spectral equations of motion of the shell-fluid system and the method of residues were employed to evaluate the mobility,and their physical interpretation was also discussed.Xu et al[6-7]have studied the vibration power flow input and transmission in a fluidfilled cylindrical shell.A technology of the spatial Fourier transforms and the inverse transforms was applied in their studies.
Practically,a cylindrical shell submerged in water is always reinforced by rings or/and bulkheads.Mead and Bardell[8]researched free vibration of a thin cylindrical shell with periodic circumferential stiffeners.When periodic structure is surrounded by the fluid field,the space harmonic analysis method presented by Mead[9]has been widely used.Using this method,Xu[10]investigated the input power flow in a periodically stiffened shell filled with fluid.Yan[11-13]also studied the characteristics of the vibrational power flow propagation and sound radiation in an infinite submerged periodic ring-stiffened cylindrical shell by the same method.Burroughs[14]studied the fluid-loaded infinite circular cylindrical with doubly periodic ring supports forced by a point excitation and gave the analytical expression of far field acoustic radiation,which established the basal thought of this kind of problem.But the model he used is comparatively simple,only the normal force between the stiffeners and the shell was considered.
When the structure is located in a dense medium such as water,there is a resultant stress field in the structure even though exists in the absence of any vibrations or acoustic loadings.The presence of this static additional stress state in the structure changes the structural response characteristics including,for example,the natural frequencies of vibration[15-16]and acoustic response of the structure[17].These effects will then subsequently result in a variation of forced vibration response of the structure as well.
The purpose of the present study is to include the hydrostatic pressure field effects in the formulation of the coupled vibro-acoustic response of submerged ring-stiffened cylindrical shells.There exists an extensive literature discussing the dynamic response of prestressed shells[18-20].Xie and Luo[21]studied the acoustic radiation properties of ring-stiffened cylindrical shells submerged in fluid by means of Hamilton’s principle and Green function,and the effects of hydrostatic pressure and rings on the acoustic radiation of the shells were also discussed.
In this paper,the space harmonic analysis is extended to investigate the input power flow induced by a cosine harmonic line force for an infinite ring-stiffened cylindrical shell submerged in water.The effects of hydrostatic pressure on the input power flow are examined.
2 Forced vibration of the coupled system
An infinite thin-walled periodic ring-stiffened cylindrical shell submerged in fluid is considered,as shown in Fig.1.The shell is characterized by its mean radius R,wall thickness h,mass density ρs,Young’s modulus E and the Poisson’s ratio μ.The density of the external fluid is ρfand the sound velocity in it is Cf.The ring stiffeners have uniform rectangular section with width b and height d,attached at x=mL(L is the stiffener spacing,m=0,±1,±2,…).The connections are rigid,so that,at each line of attachment,the shell and the stiffeners have the same linear velocity and angular velocity.The inside stiffeners may apply axial force,shear and moments on the shell.To simplify the problem,it is assumed that the stiffeners are located on the inner wall of the shell,so that their interaction with the external fluid can be ignored.
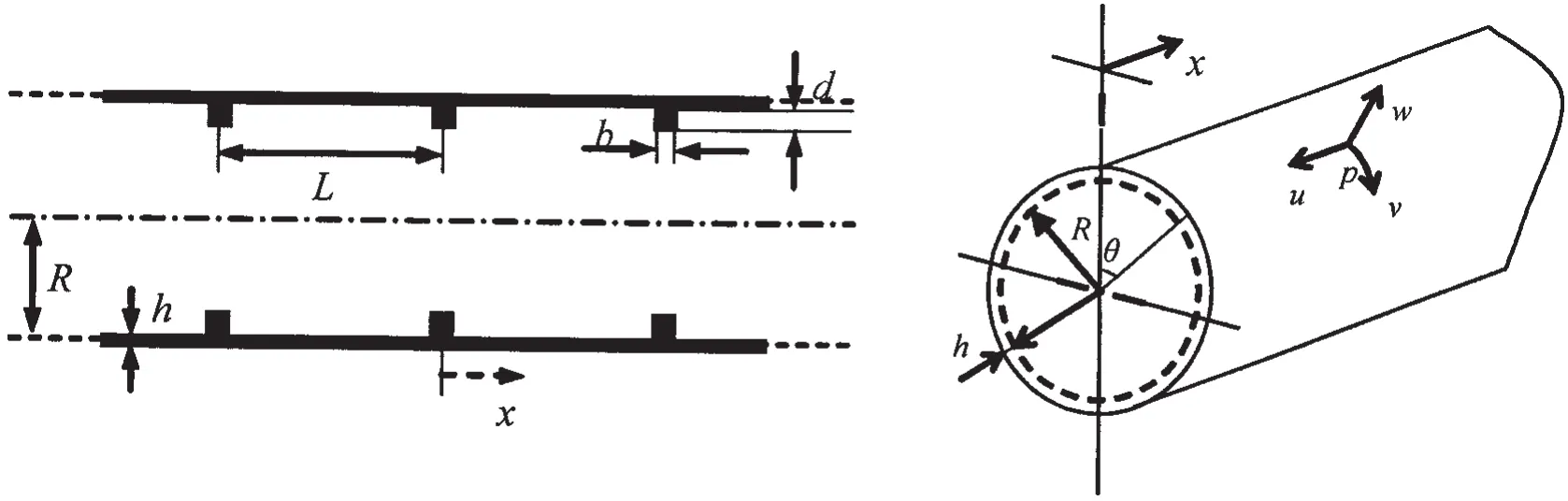
Fig.1 Periodic ring-stiffened cylindrical shell immersed in fluid and coordinate
2.1 The motion equations of the periodic shell
The shell is excited by a harmonic line pressure F,acting on x=0,expressed as

where F0is amplitude of the pressure,ω is the circular frequency,n is the circumferential model order and δ is the Dirac delta function.
The cylindrical coordinate system x,θ,( )r is adopted in the analysis shown in Fig.1.The equations of structure motion are taken from Flügge’s thin shell theory[22]as
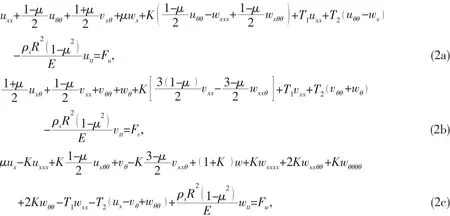

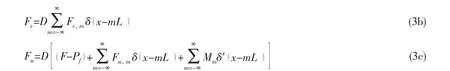
where,D=R2(1- μ2)/(Eh),δ′=dδ/dx,Pfis the acoustic pressure,Fu,m,Fv,m,Fw,mand Mmare the sideward forces and moments of the mth stiffener acting on the shell,respectively.
2.2 Fluid acoustic equations
The fluid is assumed to be non-viscous,isotropic and irrotational which satisfies the acoustic wave equation.The equation of motion of the fluid can be written by Helmholtz equation in the cylindrical coordinate system x,θ,( )r as

where the x,θ and r coordinate are the same as those of the shell.
Applying variables separation method to solve the acoustic wave equation,the associated form of the pressure field is expressed as
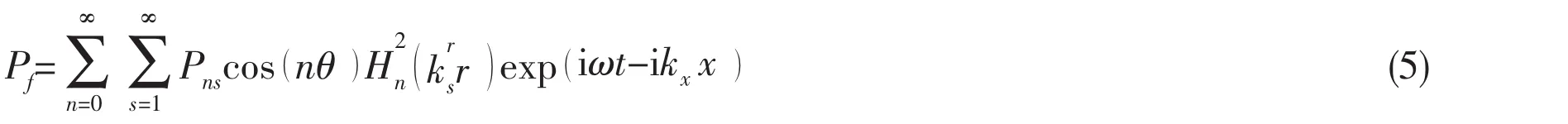
where subscript s denotes a particular branch of the dispersion curve;Pnsis the fluid acoustic pressure amplitude of every n and s;r ) is Hankel function of the second kind and order n;and kxare the radial and axial wave numbers respectively,and their relation is

where kfis the free wave number,kf=ω/Cf.
The displacement components of the shell are expressed in a travelling wave form as
where Uns,Vnsand Wnsare the displacement amplitudes in the x,θ and r directions,respectively.
As usual,the fluid velocity is continuous across the fluid-shell boundary,leading to the boundary condition

Substituting Eqs.(5)and(7c)into Eq.(8),the fluid acoustic pressure amplitude Pnsis obtained as

Introducing Eq.(9)into Eq.(5),acoustic pressure can be obtained as
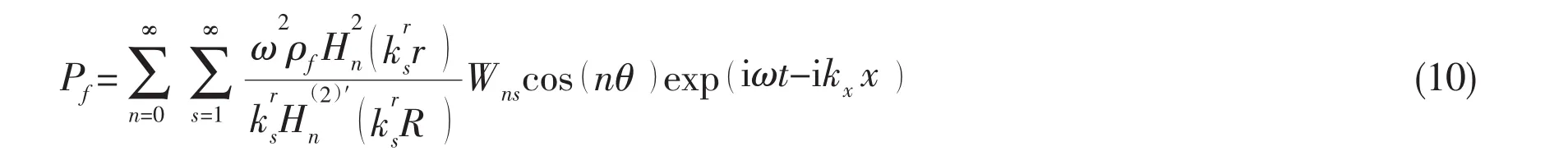
2.3 The response of the coupled system
Introducing Eqs.(7),(10)into Eq.(2)and taking the Fourier transform,the following equations are obtained in the matrix form as

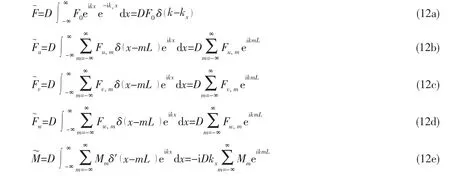
where k is axial wave number in spectral domain.
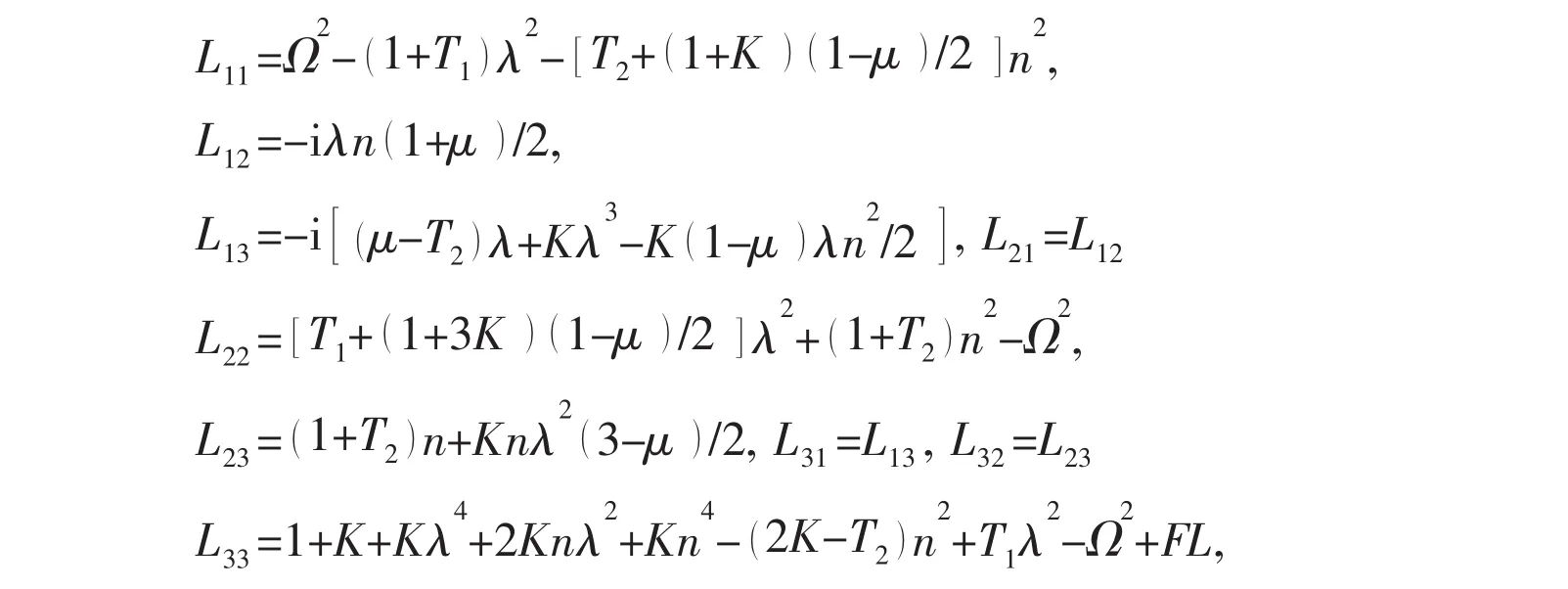


As the rings are periodic in x-axes direction,the forces in the stiffeners acting on the shell wall satisfy the periodicity condition as
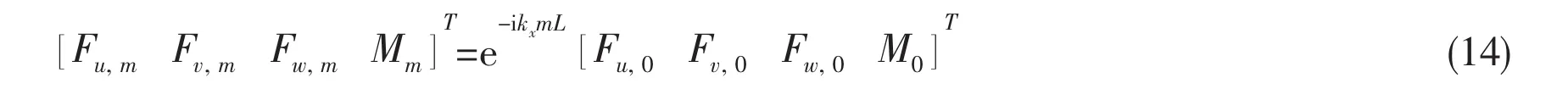
where Fu,0,Fv,0,Fw,0and M0are the forces or moments of 0th(m=0)stiffener.By using Poisson sum formula[23],the following equations can be obtained:
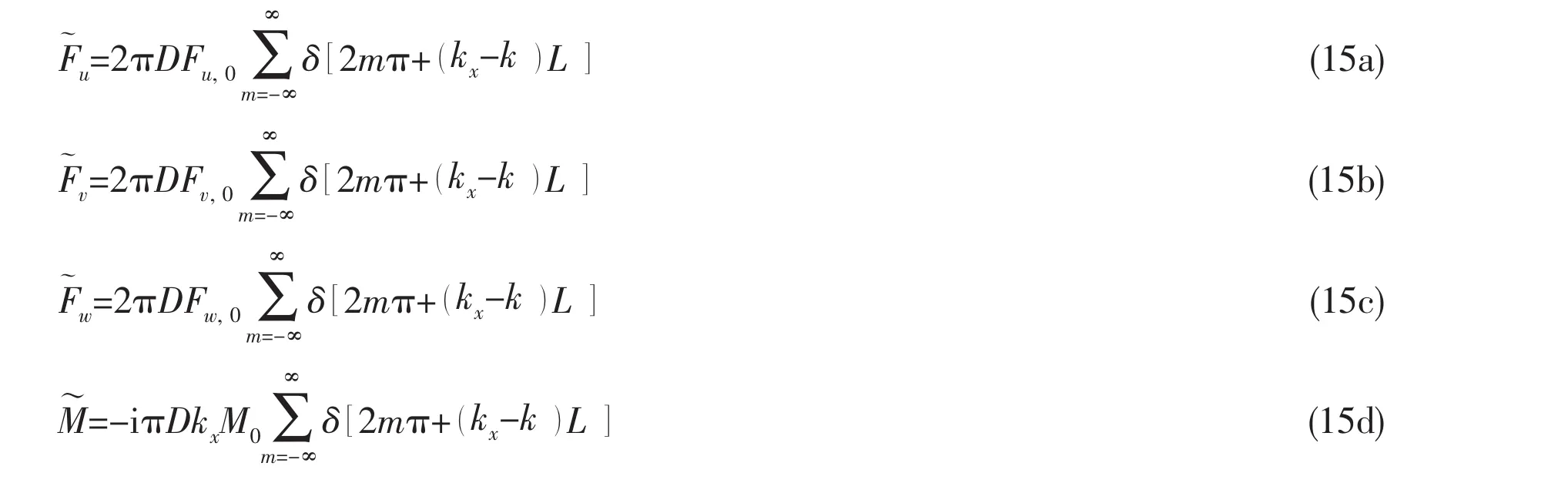
Let matrix I be the inverse of matrix L,then the spectral displacements can be obtained from Eq.(11)as follows

Taking the inverse Fourier transform to Eq.(16),the shell displacement can be obtained as:
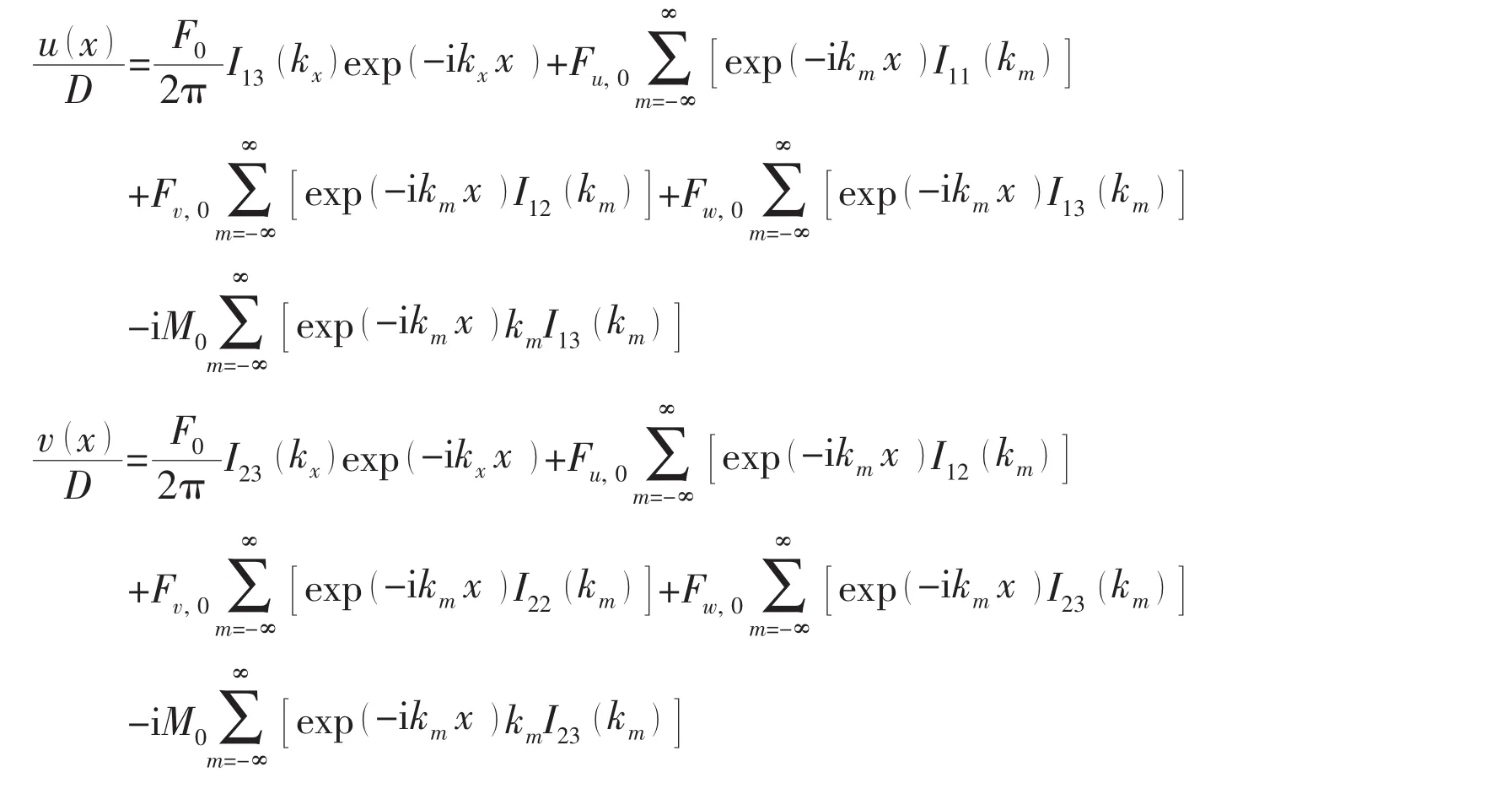
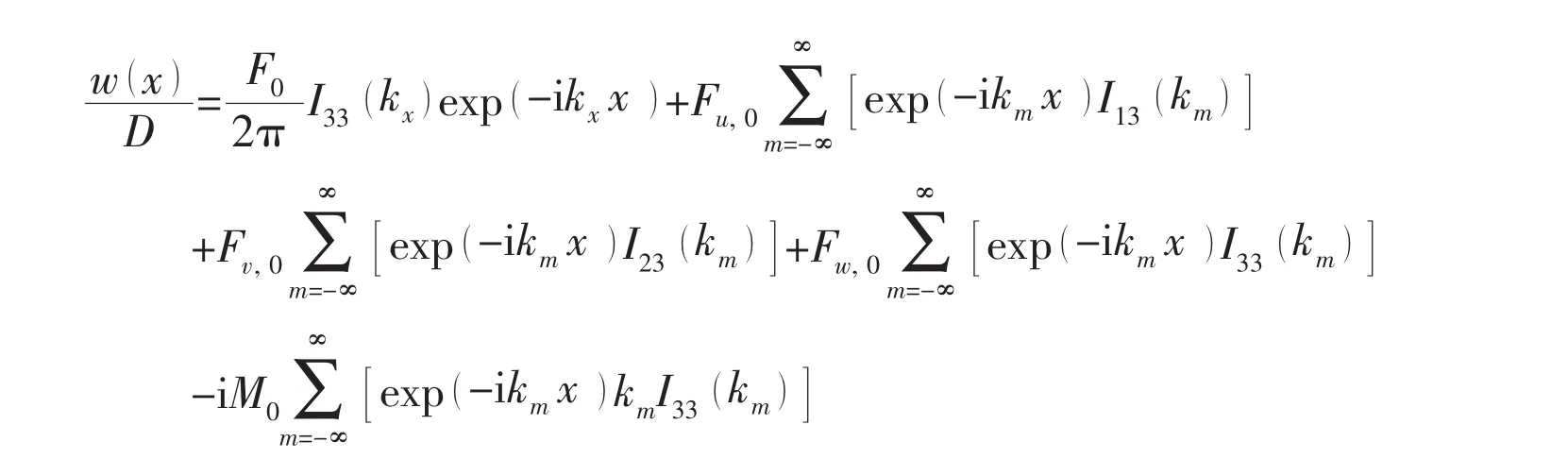
where,km=kx+2mπ/L.
Thus,the space displacement at x=0 is given by:

Once the forces and moments of the 0th(x=0)stiffener in Eq.(17)are given,the shell response to the applied pressure load F can be easily solved.Applying the compatible condition of the forces and the displacements between the shell and the stiffeners at x=0,the reaction forces can be expressed as follows[10]:
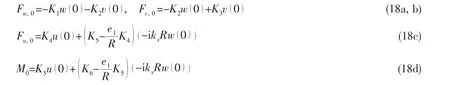
where,e1is the distance from the midsurface of the shell to the geometric center of the stiffener,K1~K6are given in the Ref.[10].
Introducing Eq.(18)into Eq.(17),the shell displacement at x=0 can be obtained in matrix form as


From Eq.(19),the displacements of the stiffened shell at x=0 can be easily solved as follows
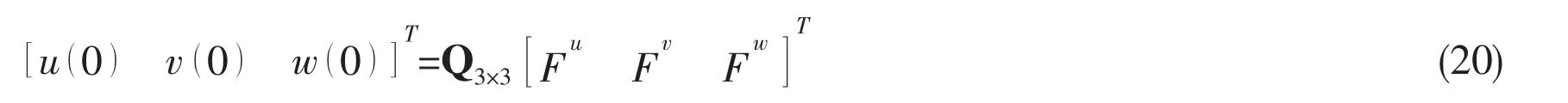
where,the elements of matrix Q can be written in terms of the element of matrix H from matrix theory and not be given for short.
2.4 The input power flow of the coupled system
For a structure excited by an external force,the magnitudes of vibration and sound radiation depend largely on the input power flow into the structure.Thus,it is important to study its characteristics of the input power flow.
According to the definition of the input power flow[1],when a cosine harmonic line force is applied to the shell wall radially,the radial response of the shell wall at x=0 can be obtained from Eq.(20).Then,the total input power flow from this driving force is defined as follows
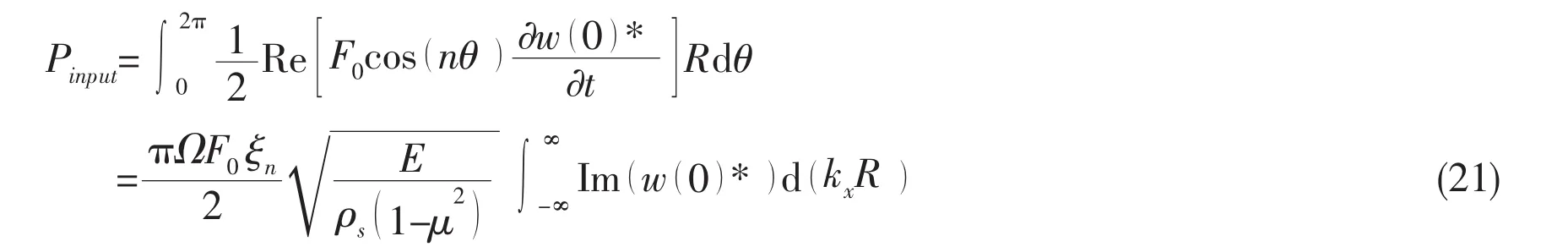
where*denotes the complex conjugate,and

The non-dimensional power flow is defined as

3 Numerical computation and result discussion
In this paper,an integrated numerical method discussed in Ref.[10]is employed to calculate the integral in Eq.(21).This method is to integrate numerically along the pure imaginary axis of the complex wave number domain in order to avoid singularities in the integrand function along the integration path.Structural damping is introduced into the shell material by modifying the Young’s modules E to be complex as E′=E 1-i( )η.Here,η is damping factor.
Numerical computations are carried out subsequently and the input power flow from a cosine harmonic line force into a periodically ring-stiffened cylindrical shell submerged in fluid is studied.The following parameters of the coupled system have been used in the computations.The shell and the stiffener adopt the same material with E=1.92×1011N/m2,ρs=7 850kg/m3,μ=0.3 and η=0.02.The thickness-radius ratio of the shell is h/R=0.02.The fluid parameters are ρf=1 000kg/m3and cf=1 500m/s.The stiffener has a rectangular cross-section with width b=2h and height d=2h,and the stiffener spacing is L=0.4R.The amplitude of radial harmonic line pressure is supposed to be F0=1N/m.
Fig.2 shows the non-dimensional input power flow P′inputinto a ring-stiffened shell and a non-stiffened shell versus the non-dimensional frequency Ω for circumferential mode order n=1,without considering the effect of hydrostatic pressure.
In some frequency bands,such as 0.68<Ω<0.76 and 1.3<Ω<1.6,the power flow input into the stiffened shell is much less than that into a shell without stiffeners.These frequency bands are named non-propagating bands,and the other frequency bands are called propagating bands in which the input power flow into the ring-stiffened shell is close to(or even exceed)that into the shell without stiffeners.It can be seen that the stiffeners greatly influence the input power flow in non-propagating bands.At Ω=0.78 and Ω=1.34,the power flow into the stiffened shell achieves its maximum,and is much more than that into an unstiffened shell.In propagating bands,the difference between the results with stiffeners and those without stiffeners is large,too.
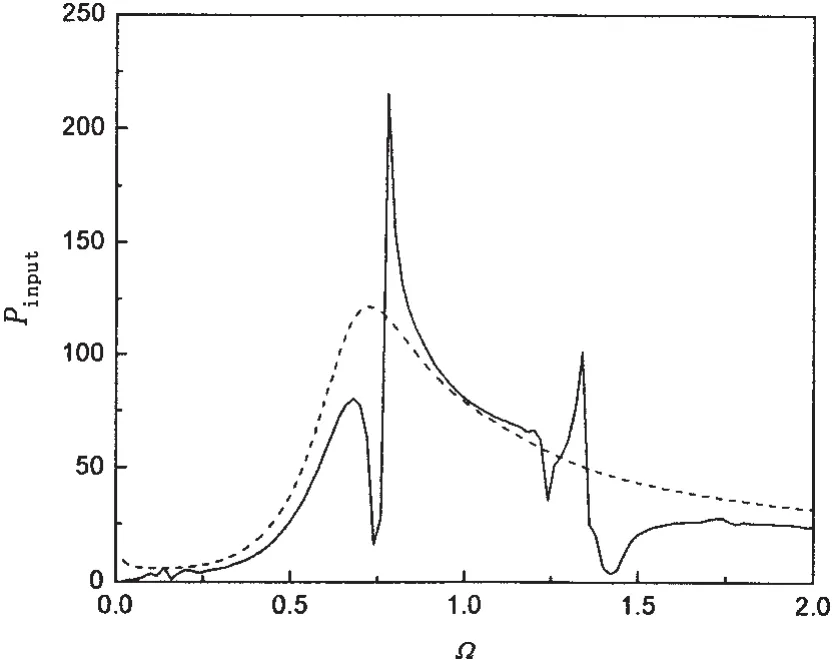
Fig.2 Input power flow into the cylindrical shell submerged in fluid for n=1—ring-stiffened shell;┄non-stiffened shell
Fig.3 shows the effect of hydrostatic pressure on input power flow into a ring-stiffened shell for circumferential mode n=0,1,and 5.There also exists propagating bands and nonpropagating bands for a stiffened shell considering the effect of external hydrostatic pressure.For n=0,the frequency bands of 0.70<Ω<0.76 and 1.3<Ω<1.6 are non-propagating bands,and the other frequency bands are propagating bands.The non-propagating bands for n=5 are the frequency bands of 0.5<Ω<0.72 and 1.4<Ω<1.6.As shown in these drawings,the curves of input power flow are shifted to left along the frequency axis mainly in non-propagating bands.It is because that the external hydrostatic pressure decreases the stiffness of the shell.Consequently,its natural frequency decreases due to the external hydrostatic pressure.The influence of hydrostatic pressure with p0=1MPa on the power flow is very small for low circumferential mode n=0 and 1.However,this influence for n=5 becomes larger.When the external hydrostatic pressure increases to p0=3MPa,the influence of hydrostatic pressure on the power flow is larger especially for the high mode n=5.
Since the hydrostatic pressure shifts the curves of input power flow into a submerged ring-stiffened shell,the peaks and valleys of the power flow are shifted.It is significant for the vibration and noise of control.
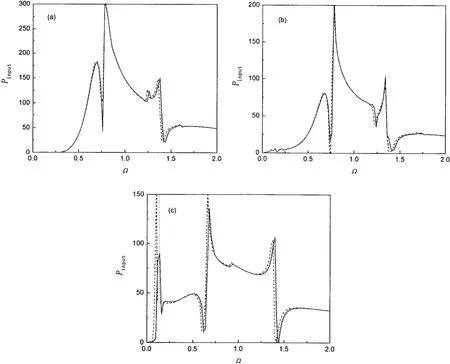
Fig.3 Effect of hydrostatic pressure on input power flow into a ring-stiffened shell(a)n=0;(b)n=1;(c)n=5;— p0=0,… p0=1MPa,┄ p0=3MPa
4 Conclusions
By adopting a periodic structure theory,a periodically ring-stiffened cylindrical submerged shell has been investigated.The input power flow for this coupled system induced by a cosine harmonic circumferential line force has been obtained and the effect of external hydrostatic pressure on the input power flow has also been examined.
There are propagating bands and non-propagating bands for a stiffened shell.The high external hydrostatic pressure influences the input power flow into the coupled system mainly in non-propagating bands.The external pressure will shift the curves of power flow to left along the frequency axis.With increasing the circumferential mode n and the external hydrostatic pressure p0,the effect of hydrostatic pressure on input power flow is more obvious.Hydrostatic pressure of a relative high value cannot be neglected when analyzing the vibration and noise of a submerged stiffened shell.
[1]Goyder H G D,White R G.Vibrational power flow from machines into built-up structures,part I:Introduction and approximate analyses of beam and plate-like foundations[J].Journal of Sound and Vibration,1980,68(1):59-75.
[2]Goyder H G D,White R G.Vibration power flow from machines into built-up structures,Part II:wave propagation and power flow in beam-stiffened plates[J].Journal of Sound and Vibration 1980,68(1):77-96.
[3]Goyder H G D,White R G.Vibration power flow from machines into built-up structures,Part III:power flow through isolation systems[J].Journal of Sound and Vibration 1980,68(1):97-117.
[4]Zhang W H,Zhang X M.Vibrational power flow in a cylindrical shell with periodic stiffeners[C]//ASME-PVP.Nashville,USA,1991.
[5]Fuller C R.The input mobility of an infinite circular cylindrical shell filled with fluid[J].Journal of Sound and Vibration,1983,87:409-427.
[6]Xu M B,Zhang X M.Vibration power flow in a fluid-filled cylindrical shell[J].Journal of Sound and Vibration,1998,218(4):587-598.
[7]Xu M B,Zhang W H.Vibrational power flow input and transmission in a circular cylindrical shell filled with fluid[J].Journal of Sound and Vibration,2000,234(3):387-403.
[8]Mead D J,Bardell N S.Free vibration of a thin cylindrical shell with periodic circumferential stiffeners[J].Journal of Sound and Vibration,1987,115(3):499-520.
[9]Mead D J,Pujara K K.Space-harmonic analysis of periodically supported beams:response to convected random loading[J].Journal of Sound and Vibration,1971,14:525-541.
[10]Xu M B,Zhang X M,Zhang W H.Space-harmonic analysis of input power flow in a periodically stiffened shell filled with fluid[J].Journal of Sound and Vibration,1999,222:531-546.
[11]Yan J,Li T Y,Liu T G,et al.Characteristics of the vibrational power flow propagation in a submerged periodic ringstiffened cylindrical shell[J].Applied Acoustics,2006,67:550-569.
[12]Yan J,Li T Y,Liu J X,et al.Space harmonic analysis of sound radiation from a submerged periodic ring-stiffened cylindrical shell[J].Applied Acoustics,2006,67(8):743-755.
[13]Yan J,Li T Y,Liu J X,et al.Input power flow in a submerged infinite cylindrical shell with doubly periodic supports[J].Applied Acoustics,2008,69(8):681-690.
[14]Burroughs B C.Acoustic radiation from fluid-loaded infinite circular cylindrical with double periodic ring supports[J].Journal of Acoustical Society of America,1984,75:714-722.
[15]Zhang Y L,Daniel G G,Jason M R.Vibration of prestressed thin cylindrical shells conveying fluid[J].Thin-Walled Structurs,2003,41(12):1103-1127.
[16]Zhang Y L,Reese J M,Gorman D G.Finite element analysis of the vibratory characteristics of cylindrical shells conveying fluid[J].Computer Methods in Applied Mechanics and Engineering,2002,191(45):5207-5231.
[17]Keltie R F.The effect of hydrostatic pressure fields on the structural and acoustic response of cylindrical shells[J].Journal of the Acoustical Society of America,1983,79(3):595-603.
[18]Meish V F,Kairov A S.Vibrations of reinforced cylindrical shells with initial deflections under nonstationary loads[J].International Applied Mechanics,2005,41(1):42-48.
[19]Arturs K.Vibration and stability of prestressed shells[J].Nuclear Engineering and Design,1972,20(1):131-147.
[20]Luo D P,Xu Z P.Vibration characteristics of submerged ring-stiffened cylindrical shells[J].Shipbuilding of China,1990(2):67-79.(in Chinese)
[21]Xie G M,Luo D P.Acoustic radiation analysis of ring-stiffened cylindrical shells in fluids[J].Shipbuilding of China,1995(4):37-45.(in Chinese)
[22]Wilhelm Flügge.Stresses in Shells[M].Second edition.Springer-Verlag,New York,1973.
[23]Mace B R.Periodically stiffened fluid-loaded plates,II:response to line and point forces[J].Journal of Sound and Vibration,1980,73:487-504.
静水压力对水下环肋圆柱壳输入功率流的影响
刘志忠,李天匀,朱 翔,张俊杰
(华中科技大学船海学院,武汉 430074)
研究了考虑静水压力时水下环肋圆柱壳在周向余弦线分布力激励下的输入功率流特性。圆柱壳体和外流场的振动分别由Flügge壳体方程和Helmholtz波动方程描述,静水压力的影响以额外应力的形式计入壳体振动方程当中。探讨了静水压力对输入功率流的影响。结果表明外部静水压力使输入功率流曲线沿频率轴往左移动,即往低频方向移动。静水压力越大,影响越大;周向模态数越大,影响越大。文中结果对水下环肋圆柱壳的振动与噪声控制有一定的指导意义。
静水压力;输入功率流;环肋圆柱壳;水下圆柱壳
O328
A
刘志忠(1980-),男,华中科技大学船海学院博士研究生;
张俊杰(1982-),男,华中科技大学船海学院博士研究生。
O328
A
1007-7294(2011)03-0301-12
date:2010-06-10
李天匀(1969-),男,华中科技大学船海学院教授,博士生导师;
朱 翔(1980-),男,博士,华中科技大学船海学院讲师;
——记华中科技大学哲学系教授欧阳康

