基于实测时间序列的非线性系统恢复力识别

许 斌,贺 佳

(1.湖南大学土木工程学院,长沙 410082;2.湖南大学建筑安全与节能教育部重点实验室,长沙 410082)

1 前言

由于结构材料自身的老化与徐变、使用荷载的变化以及各种自然和人为因素的作用,土木工程结构都不可避免地存在着不同程度损伤累积,从而导致结构使用性能降低甚至灾变行为的发生。近来,世界范围内工程事故频发,工程结构的安全事故带来巨大的生命和财产损失,进而产生较大的社会负面影响。因此,对工程结构在动力荷载作用下损伤的发生发展过程的监测与识别已经成为当前国内外土木工程领域的紧迫课题和关键科学问题之一。

一般地,随着损伤的发生和发展,结构参数也随之发生改变。因此,在过去20多年的时间里,研究人员主要将土木工程结构的损伤识别问题作为结构参数识别问题来处理,提出了系列识别方法。现有的损伤识别研究以基于动力测量的方法为主,包括时域、频域、时频域联合分析方法等[1,2]。这些土木工程结构的损伤识别方法的基本思想可以概括为以下两点。第一,用结构构件层次或者子结构刚度的降低来表征结构损伤的存在和程度;第二,运用从结构动力响应测量中抽取的结构振动频率和(或者)模态或者他们的衍生量,通过优化算法识别出结构物理参数或者对原有数值模型进行修正,所识别或者修正的参数主要是结构构件刚度或者是材料层次的弹性模量,并借此表征损伤。显然,从理论上来讲,现阶段应用最广泛的动力指纹分析法和模型修正法均基于线性假定,即在测量过程中工程结构被认为是线弹性结构,并且某些情况下要以质量已知为前提。然而,实际工程结构在动力荷载作用下损伤的发生发展过程是典型的非线性过程,伴随着结构损伤的出现,结构随即进入非线性状态,例如裂缝的发生、发展就是一个典型的非线性过程。另外,许多情况下结构的质量仅仅根据设计图纸难以准确确定。因此,运用传统的基于模型修正思想进行动力荷载作用下结构的损伤识别从方法论上说存在着不足。

事实上,与将一个非线性动力系统等价线性化,通过其刚度的变化来表述损伤程度的方法相比,结构构件的非线性恢复力特征不仅可以更直观地反映结构构件的损伤发生发展过程,而且可以定量描述结构构件在动力荷载作用下所消耗的能量,更有助于对结构的损伤进行定量评估。因此,寻找一种基于基本运动方程而不需要关于结构的线性假定的具有普遍意义的直接利用结构动力响应测量数据的结构恢复力识别的方法具有重要意义[3]。

关于土木工程结构的非线性特性识别,国外开始了初步研究。Masri和Caughy提出了恢复力曲面法,以系统位移和速度为坐标,构造非线性系统恢复力曲面,解决了单自由度动力系统的非线性参数识别问题[4]。Masri等进一步将该方法应用于解决链状多自由度非线性动力系统的识别问题[5]。针对非线性多自由度系统,Masri等基于模态转换的思想提出了完全基于结构动力响应数据测量的非线性多自由度系统的非参数化降阶模型[6,7],该方法必须将质量视为已知条件,且不能直接应用于具有滞回特性的非线性结构。运用最小二乘拟合优化算法,Toussi和Yao识别了高层结构层间力与位移随时间变化的滞回特性[8],但该方法仍然需以结构质量作为已知条件。基于单个激励和响应时程,结合最小二乘拟合算法,Mohammad等提出一种直接使用时域响应测量的线性或非线性结构物理参数识别方法[9],该方法有效识别了两种弱非线性结构的各个物理参数,然而,与通过识别结构刚度的变化来反映非线性程度、损伤大小的思路相比,结构的非线性恢复力最能反映结构自身损伤的发生和发展过程。

文章提出了一种不需要将质量视为已知条件,而是完全基于时域信号(激励和响应信号)的非线性系统恢复力的识别方法,并以安装有磁流变阻尼器(MR)的4层钢框架模型实验验证了该方法的有效性。文章研究了在结构的各自由度均受激励的完整激励情况下与仅部分自由度受激励的非完整激励情况下的实现方法。

2 时域非线性动力系统恢复力识别的基本原理

2.1 完整激励下非线性恢复力识别

在一个n个自由度的非线性结构中运动平衡方程可表示为:

结构的非线性恢复力是结构损伤状况的最直接反映,识别出式(1)中的非线性恢复力FNT,可以直观判断结构是否进入非线性阶段。

当结构的各自由度均受到激励而且激励和各自由度的响应测量已知时,为了求得FNT,可先构造一个非线性结构的等价线性结构,其平衡方程为:

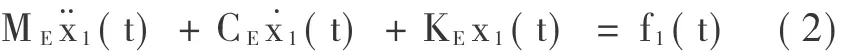
式(2)中ME、CE和KE分别为等价线性结构的质量矩阵、阻尼矩阵和刚度矩阵。对于等价线性结构,f1(t)的第i个元素可以表达成系统状态变量的线性组合[6,7]:

式(3)中,aE,ij、bE,ij、cE,ij分别表示等效质量、等效阻尼、等效刚度矩阵中等i行第j列的元素。运用优化算法,比如最小二乘算法,可以确定式(3)中的各个系数,进而得到等价线性系统的质量矩阵、阻尼矩阵和刚度矩阵。系统的质量矩阵与非线性无关,等价线性系统的质量矩阵可以作为非线性结构系统的质量矩阵的估计,于是整个非线性系统的恢复力可以根据下式确定:

一般地,至此即已达到求解恢复力的目的。在文章中非线性阻尼力由MR提供,为了验证恢复力识别结果的可靠性,运用力传感器测量了结构振动过程中MR的阻尼力大小并与识别结果进行比较。为了便于比较,需要从识别出的总非线性恢复力中除去结构自身的线弹性恢复力和粘性阻尼力。根据系统总恢复力的构成形式,MR的阻尼力为:

式(5)中,FN(t)为由MR提供的阻尼力;C、K为线性系统的阻尼和刚度矩阵。为了得到文章中线性系统的阻尼和刚度矩阵,可以将MR从非线性结构中移开,通过振动测试,运用上述方法得到。但该过程在实际中并不是必需的,在此仅为了结果比较的方便而从总的非线性恢复力中抽取出MR阻尼力。

2.2 非完整激励下非线性恢复力的识别

在实际情况下,往往很难对结构的每一个自由度进行激励,因此,上述方法必须进行改进。因为在不完整激励下,激励矩阵的秩小于结构的自由度n,从而不能直接使用最小二乘拟合求解结构矩阵。在非完整激励情况下,考虑多自由度集中质量模型,其运动方程为:

不失一般性,假设只有结构的第i个自由度上受到激励作用,则将式(6)展开并整理得:

式(7a)～(7c)中,mi表示第i个自由度上的集中质量;Vi-1,i和Si-1,i表示第i-1和i层之间的层间速度和层间位移;aj-1,j,h,l表示 Vi-1,i和 Si-1,i分别为 h次方和l次方时的待定系数;p和q为层间位移和层间速度的最高次方数,其大小视非线性程度而定。式(7a)为第i层(激励作用处)的平衡方程,式(7b)为结构顶层平衡方程,式(7c)为任意第 j层(j≠i)的平衡方程。对于式(7a),可以直接运用最小二乘法得出各个参数,而式(7b)和(7c)在等式两边同时除以mj后,运用最小二乘法也能得到各个待定系数与相应质量的比值。

根据结构各相邻质点间的相互作用力大小相等、方向相反的关系,即 aj-1,j,h,l=-aj,j-1,h,l,式(7b)和(7c)中的各个参数即可分步确定,因此,第i-1层和第i层之间的层间恢复力可以求得:

同样地,由于该层间恢复力是由结构自身的恢复力和MR阻尼力构成,则MR阻尼力的大小可以表示成:

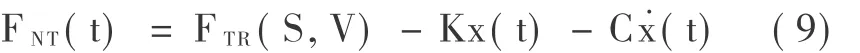
3 基于动力实验实测的非线性恢复力识别方法验证

3.1 实验模型以及动力测试

为了验证方法的有效性,设计制作了一个4层钢结构模型,并通过在结构的第4层安装磁流变阻尼器的方法模拟结构的非线性行为,实验模型如图1所示。结构平面尺寸为0.3 m×0.4 m,层高0.3 m,总高度为1.2 m,结构总质量51.41 kg。楼面板的板厚为10 mm,柱截面尺寸为30 mm×5 mm,所有柱与楼面板均采用螺栓连接。此模型可以简化成具有4个水平自由度的集中质量模型。磁流变阻尼器安装在第4层即模型的集中质量3与4之间。MR的电流为0.1 A的直流电,其产生的阻尼力的大小由力传感器直接测得。利用力锤给结构施加激励,结构的加速度响应和位移响应分别由安装在每层楼面上的加速度传感器和位移传感器测得。使用LMS数据采集系统实时记录激励力和结构的加速度、位移响应,结构的速度由实测加速度积分得到。实验采样频率为1 024 Hz。采用高通滤波,通过频率为1 Hz。图1表示实验模型、传感器安装和数据采集系统。

图1 非线性结构模型以及数据采集系统Fig.1 Nonlinear model structure and data acquisition system

3.2 完整激励下非线性恢复力识别验证

此种工况下,用一个力锤依次沿水平方向激励结构的每一层,并同时测量力锤激励力、位移和加速度响应信号。图2、图3表示的是一组位移和加速度的实测值。

图2 实测位移响应Fig.2 The displacement measurements

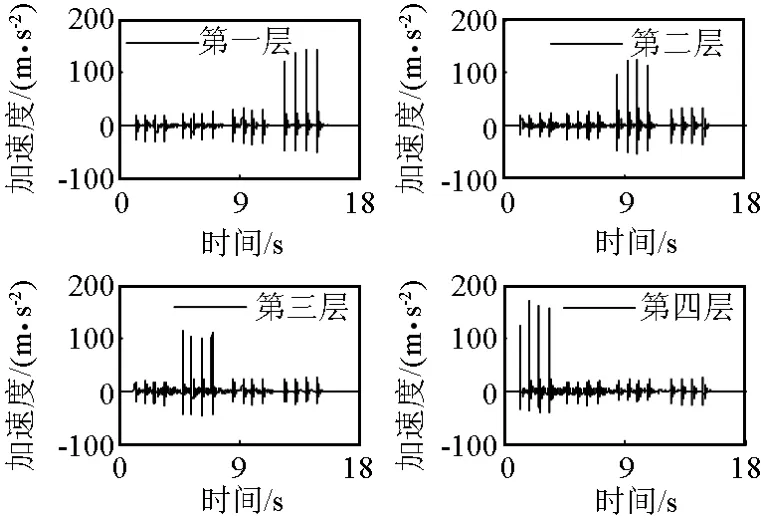
图3 实测加速度响应Fig.3 The acceleration measurements

结合以上激励和响应信号,根据式(3),运用最小二乘优化算法,可以得到用系统动力响应表示的结构各层激励,如式(10 a)～(10 d)所示。

式(10a)～(10d)中 ai、vi和 si(i=1,…,4)分别为第i层的加速度、速度和位移响应。由式(10a)～(10d)和式(3),等价线性结构的系数矩阵为:

式(11a)～(11c)的单位分别是kg、N/m和N· s/m。

此时,根据式(4)即可以直接求得结构的总恢复力。为了获得MR所产生的阻尼力的大小并与实测值进行比较,对没有安装MR的线性结构进行了动力实验。类似的,可以识别出线性结构的质量、刚度和阻尼矩阵如下:

式(12a)～(12c)的单位分别是kg、N/m和N·s/m。

由以上识别结果可知,尽管未对结构做任何假设,所识别出的线性结构质量、刚度、阻尼矩阵仍然具有较好的对称性。通过比较式(11a)～(11c)和式(12a)～(12c)可知,MR阻尼器对结构的质量和刚度影响不甚明显,这是由于MR阻尼器仅0.4 kg,相对于结构总重,其影响可以忽略不计,同时,MR阻尼器自身的特性决定了其对刚度的影响也很小。比较式(11c)和式(12c),可知MR阻尼器在结构的第3和第4集中质量之间。从而,根据式(5)即可得到MR阻尼力,其结果如图4所示。图5为实验实测的 MR阻尼力的水平分量。从图4和图5可见,识别的MR阻尼力与实测值吻合较好。

如果考察其他各层的非线性阻尼力的大小,可以发现,结构第1层至第3层的非线性阻尼力的值接近于零,表示在实验结构的第1层至第3层没有安装MR阻尼器。图6表示识别的第2层非线性阻尼力的大小,其值在整个动力测量过程中均相对较小,由此可以判断该层没有安装MR阻尼器,层间恢复力为位移和速度的线性组合,层间结构未表现出非线性行为。第1层与第3层的结果类似,由于篇幅限制未列出。由此可见,该算法不仅能准确地确定动力荷载作用下结构的非线性响应区域,同时能定量地识别出结构非线性层间滞回特性。

图4 识别的第4层MR阻尼器阻尼力Fig.4 The identified MR force on the 4th floor

图5 实测的第4层MR阻尼器阻尼力Fig.5 The measured MR force on the 4th floor

3.3 非完整激励下非线性恢复力识别验证

为了验证改进的算法的可靠性,进行了相应的动力测试实验。实验中力锤仅沿水平方向作用在结构的第3层,同时采集位移和加速度信号。实测位移、加速度信号分别如图7、图8所示。

从理论上说,根据式(7a)～(7c),S和V的最高次方数(即p和q)取得越高,越能够更好地模拟结构的非线性。然而,实际工程中,次方数越高,运用最小二乘算法时噪声的影响也越大,综合考虑,文中取p+q=3(p,q均为整数)。

图6 识别的第2层MR阻尼器阻尼力Fig.6 The identified MR force on the 2nd floor

图7 实测位移响应Fig.7 The displacement measurements

图8 实测加速度响应Fig.8 The acceleration measurements

运用最小二乘拟合优化算法,首先识别第3层平衡方程中的各个系数,然后依次识别其余各层系数。因此,根据式(8),结构各层层间恢复力为:

式(13)中Vi=vi-vi-1和Si=si-si-1表示相邻两层间的层间速度和层间位移;FTR(i,i-1)表示第i层和第i-1层的层间恢复力。得到各层层间恢复力的表达式后根据式(9)可以确定MR阻尼力大小。图9、图10分别表示识别的和实测的第4层MR阻尼力。比较图9与图10可见,非完整激励下识别出的MR阻尼力的大小与实测值基本吻合。通过多项式表达的恢复力识别结果与位移的关系曲线略显光滑。

图9 识别的第4层MR阻尼器阻尼力Fig.9 The identified MR force on the 4th floor

图11所示为第2层MR阻尼力的识别结果,从图中可见,第2层的MR阻尼力相对较小,类似的结果也可以在第1、3层得到。可以推断结构的第1层至第3层没有安装MR阻尼器,相应层表现出线性行为,识别结果与实际情况相符。可见,在非完整激励情况下所提出的改进的算法仍然不失为一种识别结构非线性恢复力的有效的方法。

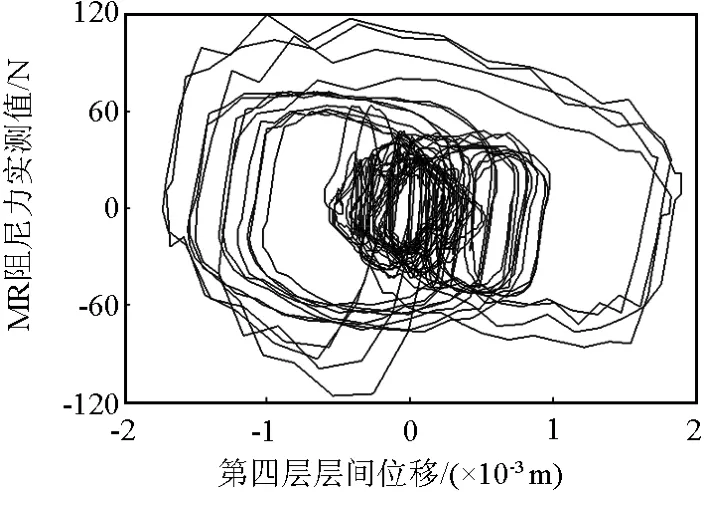
图10 实测的第4层MR阻尼器阻尼力Fig.10 The measured MR force on the 4th floor

图11 识别的第2层MR阻尼器阻尼力Fig.11 The identified MR force on the 2nd floor

4 结语

基于结构的激励和动力响应信号,运用文章所提出的方法可以对多自由度非线性系统的非线性恢复力进行有效识别。针对不同的激励形式,文章分别提出了识别非线性恢复力的具体实现方法。该方法不需要已知结构质量,也不需要对识别对象的拓扑结构进行假设,其理论依据为运动平衡方程,具有一般性。通过在一个4层钢结构模型中安装MR阻尼器模拟结构非线性,运用在完整激励和非完整激励下的动力实验验证了该方法的可行性。结果表明,该方法是一种有效可行的结构非线性行为识别方法,能有效地识别出结构在动力荷载作用下的非线性恢复力。该方法能基于工程结构在动力荷载作用下的监测数据对结构的非线性恢复力进行定量识别,进而可直观体现结构的非线性行为的发生和发展过程。该方法将在结构健康监测和损伤评估中得到有效应用。

文章所提出的两种识别方法均运用了结构各个自由度上的加速度、速度和位移测量时间序列,然而实际工程中,最易获得的观测值是加速度,因此,对于仅有加速度实测值或结构响应观测值有限的情况,需要对该方法进行进一步拓展。

[1]Doebling S W,Farrar C R,Prime M B.A summary review of vibration-based damage identification methods[J].Shock and Vibration Digest,1998,30(2):91-105.

[2]李国强,李 杰.工程结构动力检测理论与应用[M].北京:科学出版社,2002.

[3]Zhou R,Xu B,He J,et al.Data-based hysteretic performance identification for a nonlinear structure equipped with MR damper[C]//Proceedings of the Tenth International Symposium on Structural Engineering for Young Experts.2008,2:1516-1521.

[4]Masri S F,Caughey T K.A nonparametric identification technique for nonlinear dynamic problems[J].Journal of Applied Mechanics,ASME,1979,46(2):433-447.

[5]Masri S F,Sassi H,Caughey T K.Nonparametric identification of arbitrary nonlinear system [J].Journal of Applied Mechanics Transportation,1982,49:754-767.

[6]Masri S F,Caffery J P,Caughey T K,et al.A general data-based approach for developing reduced-order models of non-linear MDOF systems[J].Nonlinear Dynamics,2005,39:95-112.

[7]Masri S F,Tasbihgoo F,Caffery J P,et al.Data-based model-free representation ofcomplex hysteretic MDOF systems [J].Structural Control&Health Monitoring,2006,13:365-387.

[8]Toussi S,Yao T P.Hysteretic identification of existing structures[J].Journal of Engineering Mechanics,ASCE,1983,109(5):1189-1202.

[9]Mohammad K S,Worden K,Tomlinson G R.Direct parameter estimation for linear and non-linear structures[J].Journal of Sound and Vibration,1992,153(3):471-499.