寿命期内预应力混凝土连续梁体系可靠度分析

田 浩，陈艾荣

(1.同济大学 桥梁工程系，200092 上海，tianhao－8@163.com;2.浙江省交通科学研究所，310006 杭州)

寿命期内预应力混凝土连续梁体系可靠度分析

田 浩1，2，陈艾荣1

(1.同济大学 桥梁工程系，200092 上海，tianhao－8@163.com;2.浙江省交通科学研究所，310006 杭州)

为了模拟氯离子侵蚀环境作用时寿命期内预应力混凝土桥梁的结构性能演变过程，建立了一种基于概率和有限元的寿命期内预应力混凝土桥梁性能演变分析方法.首先，明确了退化过程中的3个关键时刻并给出其计算公式;其次，在重点解决退化过程分析中的材料力学性能退化、截面面积削弱以及结构整体力学性能演变等问题模拟方法的基础上编写了耐久性分析程序CBDAS;最后，结合分析程序CBDAS、Monte－Carlo模拟以及体系可靠度分析程序建立了预应力混凝土桥梁时变体系可靠度分析方法.以一座预应力混凝土连续梁桥为对象，利用时变体系可靠度研究其在氯离子侵蚀作用时寿命期内的结构性能演变规律.

预应力混凝土桥梁;寿命期;性能演变;Monte-Carlo模拟;时变体系可靠度

氯离子侵蚀环境作用会引起混凝土桥梁性能退化，减少结构的使用寿命，需对其进行耐久性设计.其中首要解决的问题是如何模拟寿命期内混凝土桥梁的结构性能演变过程.此外，由于结构构造、荷载和环境条件中固有的随机性，结构性能演变分析应是基于概率的.到目前为止，众多学者开展了基于概率的不同类型结构性能演变分析［1－5］，通过失效概率、可靠度或冗余度等性能指标研究了不同结构的性能演变过程.但是在现有研究中主要存在2个问题:结构的极限状态方程均以显式函数表示，而对于混凝土连续梁等超静定体系结构其极限状态方程是隐式的，需要利用有限元方法求解;研究多集中在承载能力极限状态(钢筋混凝土桥梁的抗弯和抗剪承载力)而很少涉及正常使用极限状态(预应力混凝土桥梁的混凝土压应力等).

本文建立了一种基于概率和有限元的寿命期内预应力混凝土桥梁性能演变分析方法.首先，明确了退化过程中的3个关键时刻;其次，在给出退化过程中关键力学问题模拟方法的基础上编写了耐久性分析程序 CBDAS;最后，结合 CBDAS、Monte-Carlo模拟以及体系可靠度分析程序建立了预应力混凝土桥梁时变体系可靠度分析方法.以一座预应力混凝土连续梁桥为对象，利用时变体系可靠度研究其在氯离子侵蚀作用下寿命期内结构性能演变规律.

1 退化过程中的关键时刻

混凝土桥梁的退化过程可通过3个关键时刻:钢筋开始锈蚀时刻t1、保护层开始开裂时刻t2以及保护层完全剥落时刻t3划分为4个阶段.

1.1 钢筋开始锈蚀时刻

退化过程的第一阶段由施工过程结束时刻(即成桥时刻)开始到钢筋表面的氯离子浓度累积到钢筋即将开始锈蚀时刻t1为止，该阶段也可称为氯离子侵蚀阶段.t1可表示为［6］

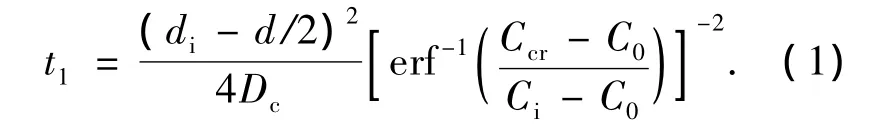
式中:di普通钢筋形心到混凝土表面的距离(mm)，d为普通钢筋的直径(mm)，Dc为氯离子扩散系数(mm2/a)，Ccr为钢筋锈蚀临界氯离子质量分数，C0为混凝土中氯离子质量分数，Ci为混凝土中初始氯离子质量分数.为了考虑氯离子扩散系数随时间的变化，文献［7］根据现场及试验实测数据修正了式(1)，即

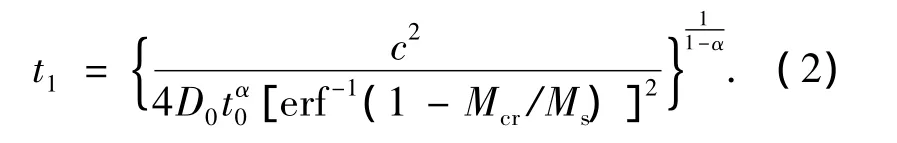
式中:c为混凝土保护层厚度(mm)，D0为氯离子扩散系数(mm2/a)，t0为结构建成至检测时所经历的时间(a)，α为D0的时间效应系数，Mcr为钢筋锈蚀临界氯离子质量浓度(kg/m3)，Ms为混凝土表面氯离子质量浓度(kg/m3).本文将利用式(2)预测钢筋锈蚀开始时刻t1.

1.2 保护层开始开裂时刻

退化过程的第2阶段可定义为钢筋锈蚀产物膨胀阶段.从钢筋开始锈蚀时刻t1到钢筋锈蚀产物的膨胀即将引起混凝土保护层开裂时刻t2，可表示为［8］

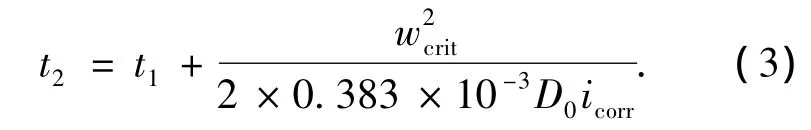
式中:wcrit为临界锈蚀量(kg/m)，icorr为锈蚀速率(μA/cm2).据笔者所知，由于其理论公式难以用于有限元计算，在以往研究中wcrit通常是依据专家的经验假定一个数值.因此，本文采用一个基于现场和实验数据拟合的实用公式求解t2［7］

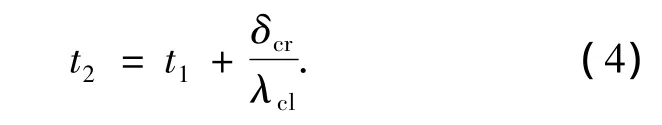
式中:δcr为保护层即将开裂时的钢筋临界锈蚀深度(mm)，λcl为保护层开裂前钢筋年平均锈蚀率(mm/a).

1.3 保护层完全剥落时刻

在退化过程的第3阶段钢筋锈蚀不断加深直至混凝土保护层完全剥落时刻t3，此后进入第4阶段.在第4阶段中假设钢筋继续锈蚀而混凝土截面不再进一步削弱，根据这一假定结构性能将继续退化直至结构到达极限状态或设计使用寿命，意味着整个退化过程的结束.据笔者所知，在现有的混凝土桥梁退化过程模拟中均未考虑保护层完全剥落时刻t3，但这个时间点在分析中是十分必要的，因为:为了模拟混凝土桥梁的完整退化过程混凝土保护层开裂后的性能演变过程也应包含在内，而不仅仅是把保护层开裂时刻t2作为结构寿命的终点;同混凝土保护层相比，保护层内的混凝土截面由于包裹了许多钢筋因此不容易引起开裂剥落.本文采用一个利用实验和工地现场数据拟合的公式计算t［7］3

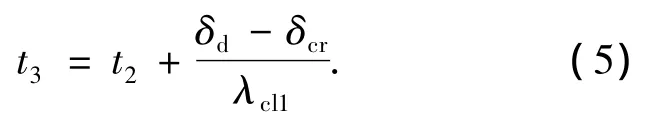
式中:δd为保护层完全剥落时的钢筋临界锈蚀深度(mm)，λcl1为保护层开裂后钢筋年平均锈蚀率(mm/a).

2 关键力学问题

2.1 施工过程

施工过程中的主要力学问题包括:结构体系转换、预应力效应以及混凝土徐变收缩［9－10］.混凝土桥梁施工方法众多，例如:满堂支架浇筑法、悬臂浇筑法、简支变连续法以及顶推施工法等.在这些方法中应着重解决以下力学问题:增加混凝土构件、增加预应力钢筋、添加或删除临时约束、不同材料截面的组合以及模拟挂蓝施工过程等.根据现有分析方法笔者编写了可考虑以上力学问题的混凝土桥梁施工过程分析模块［11］.预应力效应采用等效荷载法模拟［10］.

2.2 退化过程

退化过程中的主要力学问题包括:材料力学性能退化、截面面积削弱以及整体力学性能演变.

2.2.1 材料力学性能退化

模拟材料力学性能退化的关键是选取能够较准确反映材料强度、弹性模量和剪切模量等力学性能指标退化规律的数学模型.通过对试验和现场数据的分析，国内外学者建立了许多混凝土和普通钢筋的力学性能退化模型［12－14］.但是，针对预应力钢筋锈蚀的研究则相对较少［3，15－16］.考虑到预应力钢筋的高强度、冶金特性以及管道保护的作用，文献［3］假定预应力钢筋的锈蚀率将通过普通钢筋的锈蚀率来确定，即某时刻预应力钢筋的锈蚀率设定为相同条件下普通钢筋锈蚀率的75%.笔者也采用该假定来模拟预应力钢筋的锈蚀过程.根据现有的研究成果，笔者在分析程序［11］中建立了材料力学性能退化模型数据库，用户可根据自己的实际需要选取相应的退化数学模型.同时在分析程序中还预留接口，待今后出现更加合理的退化数学模型时可以对模型库进行补充和完善.

2.2.2 截面面积削弱

在氯离子侵蚀作用下，混凝土截面、普通钢筋截面和预应力钢筋截面都有可能被削弱.

1)混凝土截面.由于桥梁同一截面的不同方向可能拥有不同的环境条件和设计参数，因此混凝土截面形状信息以其边缘为基本单位生成.由图1上半部分可以看出对于混凝土桥梁常使用的箱形截面其边缘数量正好等于节点数量.所以，边缘信息将通过一组控制节点信息生成，截面的几何特征(如:面积、形心和惯性矩等)将利用控制节点的坐标得到.这里注意截面外表面和内表面的节点和边缘序号顺序分别为逆时针和顺时针.

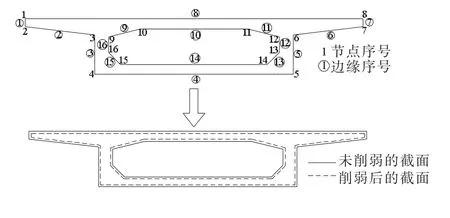
图1 混凝土截面削弱

在以边缘为单位的基础上，混凝土截面的退化过程将用边缘的移动来模拟:首先，根据结构某时刻的时间信息和钢筋锈蚀模型计算普通钢筋的锈蚀量;其次，根据普通钢筋的锈蚀量得到混凝土边缘的削弱深度;再次，根据相邻两条边缘的移动距离得到一个新的控制节点并由此得到一组新的控制节点;最后，利用新的控制节点计算削弱后的混凝土截面几何特征.图1的下半部分给出了混凝土截面的削弱过程.

2)普通钢筋截面.与混凝土截面类似，普通钢筋也是以混凝土边缘为基本单位模拟.每条混凝土边缘包含一组普通钢筋信息:普通钢筋数量、普通钢筋直径，混凝土保护层厚度以及普通钢筋形心到整个混凝土截面形心的距离.利用所有混凝土边缘上的普通钢筋信息可以计算整个截面上普通钢筋的截面几何特征.普通钢筋截面的削弱过程为:根据各自的环境条件、时间信息以及退化模型求解每条混凝土边缘上普通钢筋的锈蚀率以此得到普通钢筋削弱的面积;根据每条混凝土边缘上锈后的普通钢筋截面计算整个截面上普通钢筋的截面几何特征.

3)预应力钢筋截面.在分析中，预应力钢筋是通过在输入数据中的线形信息和结构中的插入点来模拟.利用预应力钢筋线形和混凝土截面形状求出预应力钢筋到4边混凝土边缘的距离.考虑预应力钢筋截面锈蚀过程时，利用与普通钢筋相同的方法求出其锈蚀率从而得到锈后面积.分析中所有预应力钢筋的形心始终保持不变.

2.2.3 整体力学性能演变

整体力学性能演变分析中主要有2个问题:削弱截面的自重损失和削弱截面内力的重分布.

1)削弱截面的自重损失.削弱截面的自重损失分析与常规分析中的自重作用模拟类似，虽然所有混凝土边缘的移动都会引起截面面积的削弱，但是其外表面的顶部边缘和内表面所有边缘的移动将不会引起自重削弱，因为这些边缘削弱的混凝土仍将作为荷载作用在结构上.同理，由于普通钢筋和预应力钢筋均包裹在混凝土截面内，因此其锈蚀产物的自重仍将作用在结构上.

2)削弱截面的内力重分布.削弱的混凝土截面、普通钢筋截面和预应力钢筋截面上原先作用的内力需要重分布到锈后结构上.这一力学问题的模拟方法见图 2.图中 Ic，c，Ic和 Ic，h分别为削弱的、削弱前以及削弱后混凝土截面的形心，Nc，c，Nc和 Nc，h分别为相应的混凝土截面承担的内力，通过Nc，c可以生成削弱混凝土截面上内力引起的荷载Fc，c.同理，可生成削弱普通钢筋和预应力钢筋截面的内力引起的荷载 Fs，c和 Fp，c.最终，组合 Fc，c、Fs，c和 Fp，c将形成削弱截面上的内力引起的荷载Fc.

图2 削弱截面的内力重分布

2.3 分析程序CBDAS

利用退化过程中3个关键时刻的计算模型以及关键力学问题的模拟方法，笔者建立了寿命期内混凝土桥梁性能演变分析方法并编写了基于有限元的分析程序 CBDAS［11］(Concrete Bridge Durability A-nalysis System).CBDAS共包括8个子系统，见图3.

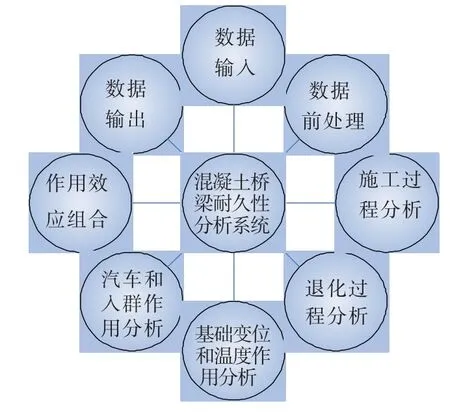
图3 CBDAS组成

3 时变体系可靠度

3.1 时变抗力和响应

利用Monte-Carlo模拟方法和分析程序CBDAS，笔者编写了分析程序MCSTRL(Monte-Carlo Simulation of Time-variant Resistance and Load effect)，图4给出了MCSTRL的分析流程.这里采用了Kolmogorov-Smirnov试验法(K-S检验)来确定时变抗力R(t)和时变响应S(t)的分布类型和统计参数.

3.2 体系可靠度

求解混凝土桥梁时变体系可靠度的具体步骤为:将整体结构划分为若干构件;利用基于Monte-Carlo模拟的分析程序MCSTRL求出时变抗力R(t)和效应S(t)的分布类型和统计参数;通过串－并联模型［17］定义结构的体系失效模型;利用程序RELSYS［18］计算体系可靠度.时变体系可靠度的具体算法见图5.

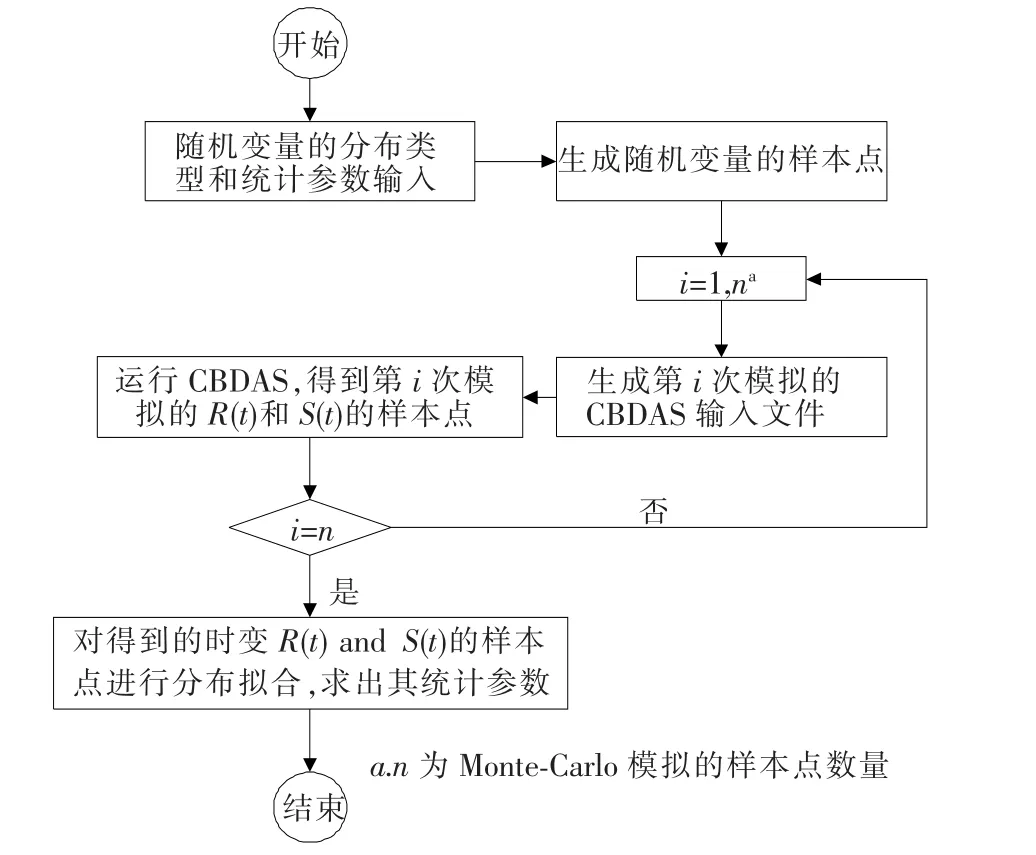
图4 MCSTRL的分析流程

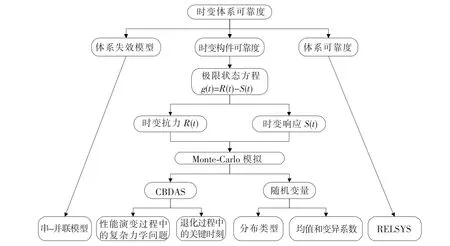
图5 时变体系可靠度分析

4 数值算例

4.1 模型介绍

选取一座3×25 m三跨等高度钢筋混凝土连续箱梁桥为研究对象(图6)，该桥位于上海地区，采用满堂支架施工法.表1给出了模型分析中来自结构构造、材料特性、荷载和环境条件中的随机变量的统计参数.

4.2 体系失效模型

利用结构－构件划分方法［11］，模型梁被划分为21个构件，每跨7个构件.考虑承载能力极限状态下的弯曲破坏和剪切破坏2种极限状态以及正常使用极限状态下的混凝土压溃和混凝土开裂2种极限状态.体系失效模型见图7，该失效模型为一串联体系，失效概率P(R＜S)意味着任意一个构件的荷载效应Si(t)超过其抗力Ri(t)的可能性.

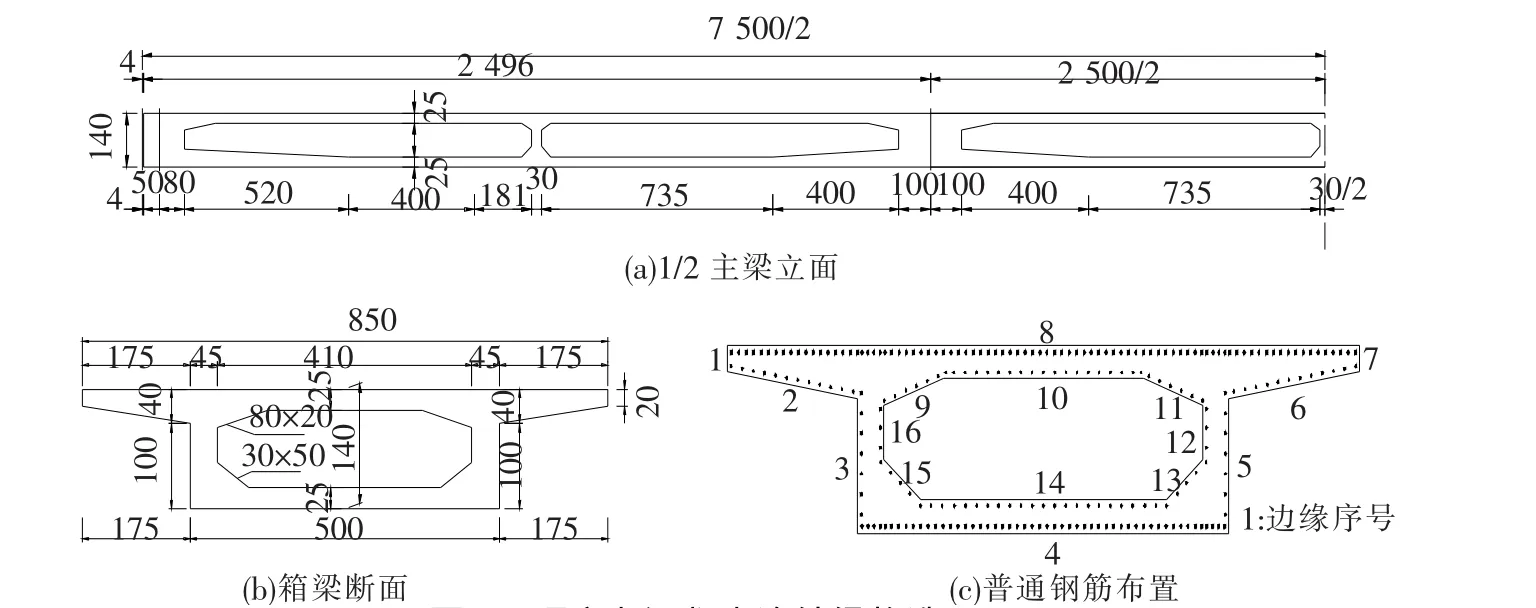
图6 预应力混凝土连续梁构造(cm)

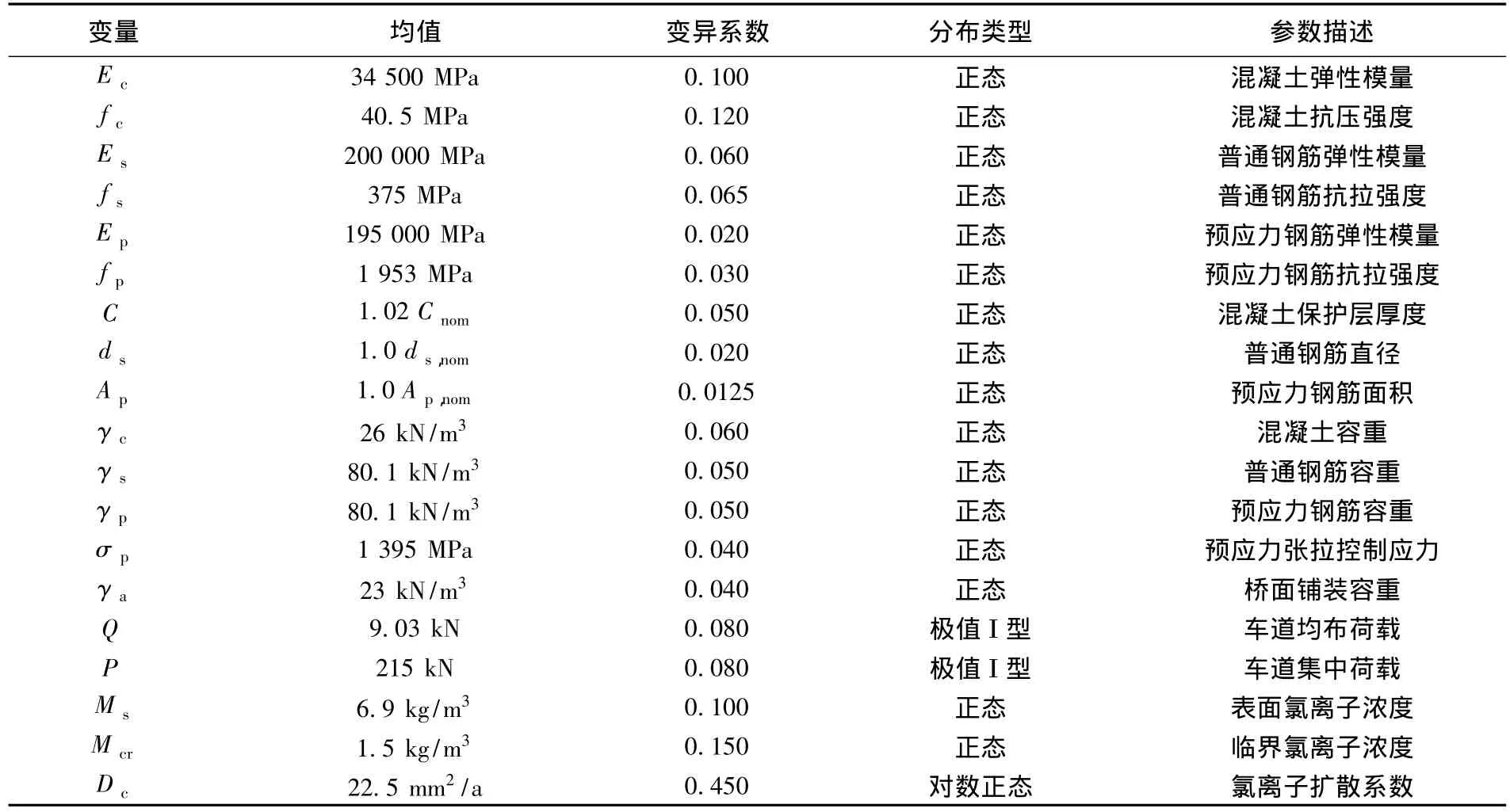
表1 随机变量的统计参数

4.3 结果分析

假定设计使用寿命为100 a，10 a为一计算子步骤.Monte-Carlo模拟的样本点数量为5 000.抗力之间以及抗力与荷载效应之间假定统计独立，相邻的2个构件之间同种荷载效应的相关系数假定为0.5.表2给出了结构不同构件的弯矩和压应力在不同时间点的最佳拟合分布类型，考虑对称性这里仅列出一半构件.表中出现了正态分布(N)、对数正态分布(LN)、Gamma分布(G)以及Weibull分布(W)，说明不同构件的结构响应可能拥有不同的分布类型，即使同一构件在不同时间点的分布类型也可能不同.

图8给出了构件4的弯矩在不同时间点处经Monte-Carlo模拟得到的柱状图及拟合分布类型，其拟合的最佳分布分别为正态、正态、Gamma和对数正态.

图7 体系失效模型

图9给出了构件4的混凝土压应力在不同时间点处的柱状图及拟合分布类型，其拟合的最佳分布分别为正态、正态、Weibull和Weibull.

图10给出了承载能力极限状态下关键构件和体系可靠度随时间的演变规律.在成桥初期，最小构件抗剪可靠度βmin，2大于最小构件抗弯可靠度βmin，1，但是在成桥40 a后前者开始小于后者.因此，结构的体系可靠度在成桥后40 a内由最小构件抗弯可靠度决定而在剩余寿命期内将受抗剪可靠度控制.在整个寿命期内，最小构件抗弯可靠度和抗剪可靠度始终产生于构件4和1(也就是边跨跨中和中跨靠近中支点1/4跨径位置)，前者是弯曲的关键位置而后者并不是，说明在进行体系可靠度分析时应包括所有构件而不仅仅是几个关键构件(如跨中截面的弯曲状态和支点截面的剪切状态).此外，最小构件抗剪可靠度在成桥10～40 a并非单调变化，这是由于在此时间段内抗剪承载能力几乎保持不变而剪力效应非单调变化造成的.此外，由于混凝土截面腹板处箍筋大量损失引起结构抗剪能力的严重削弱，结构体系可靠度在成桥100 a时下降到1.2，因此需要采取相应加固措施来提高结构的抗剪承载能力.

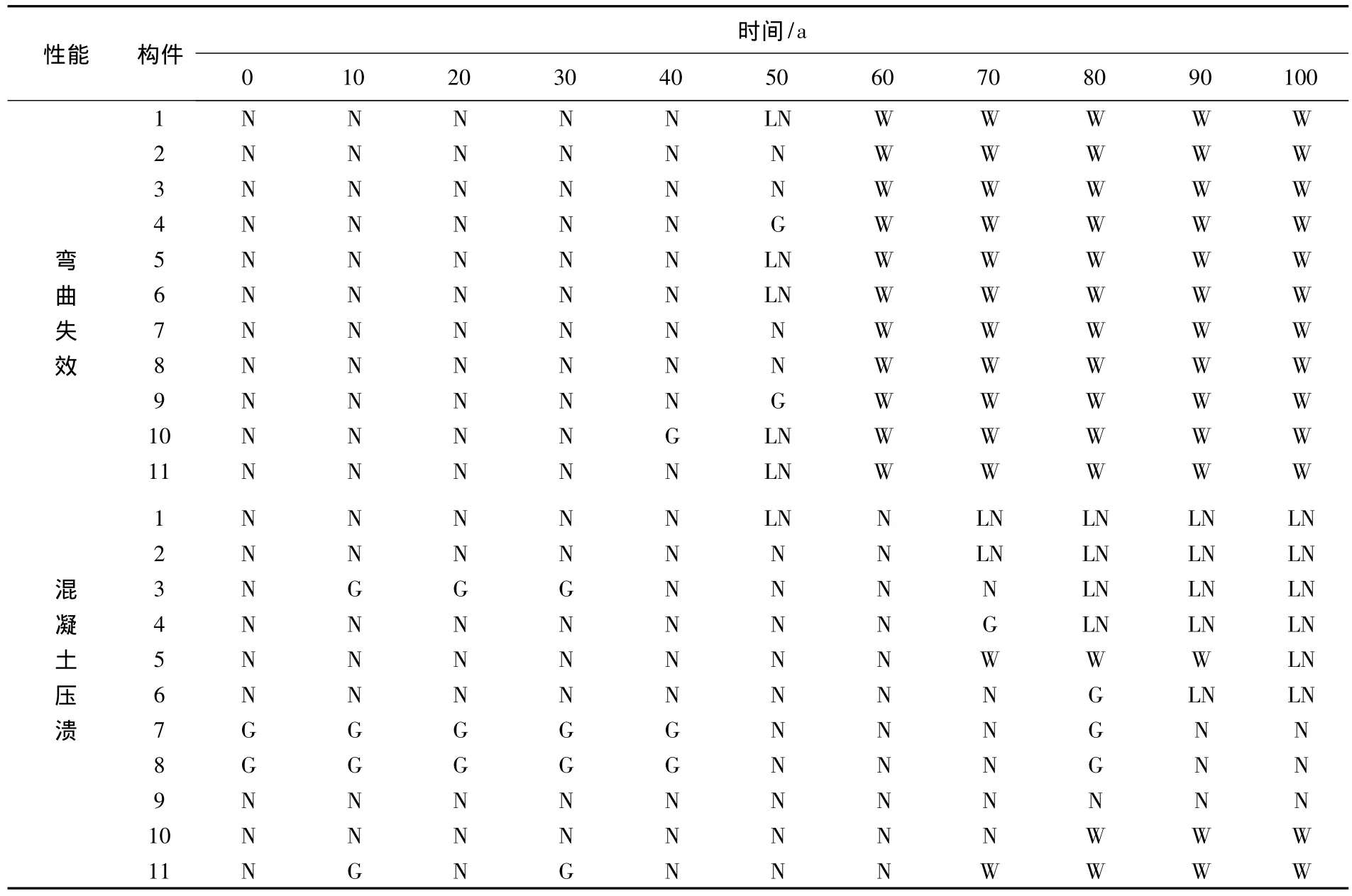
表2 不同构件弯矩的分布类型

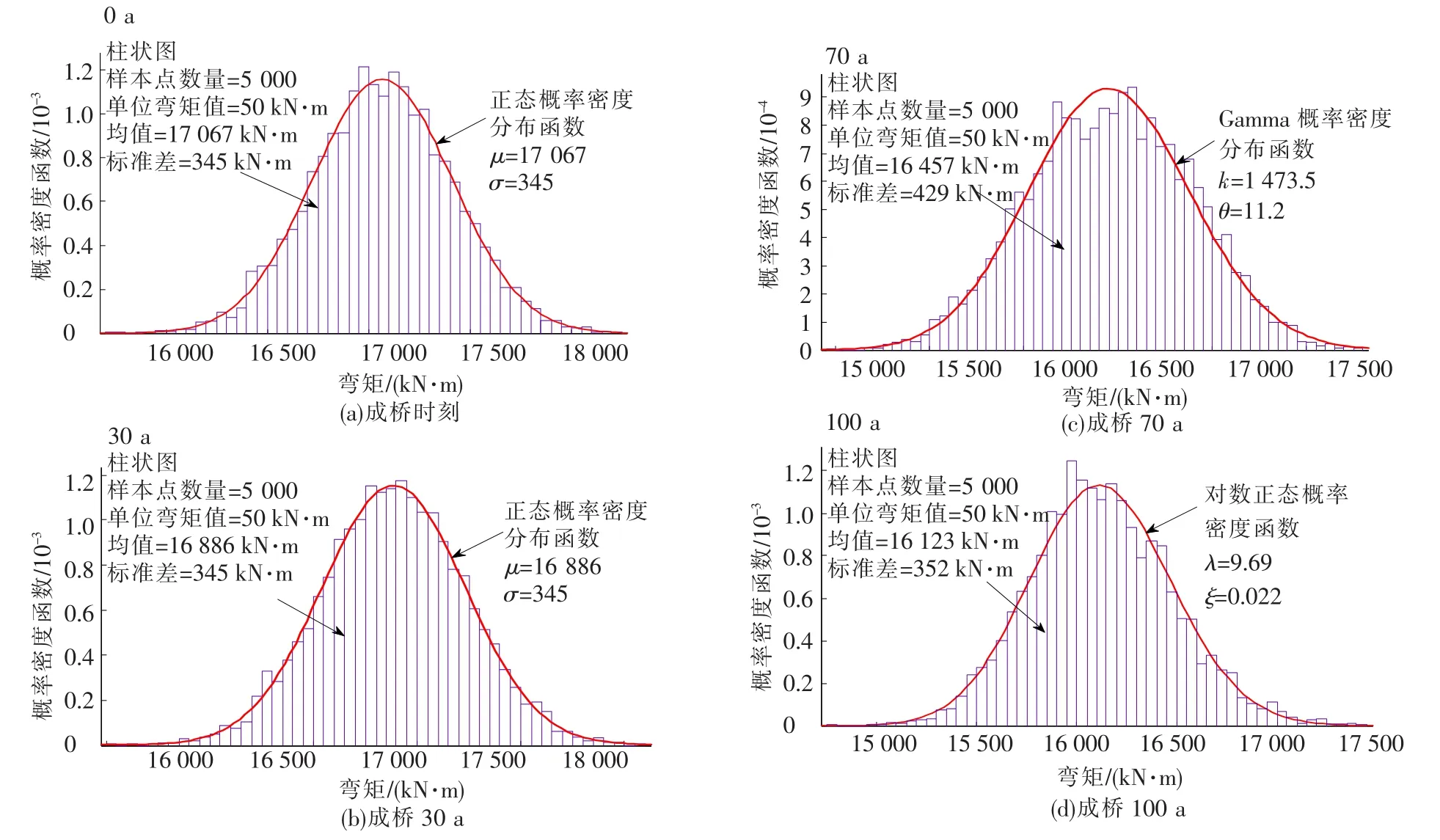
图8 构件4弯矩的柱状图及其概率密度函数

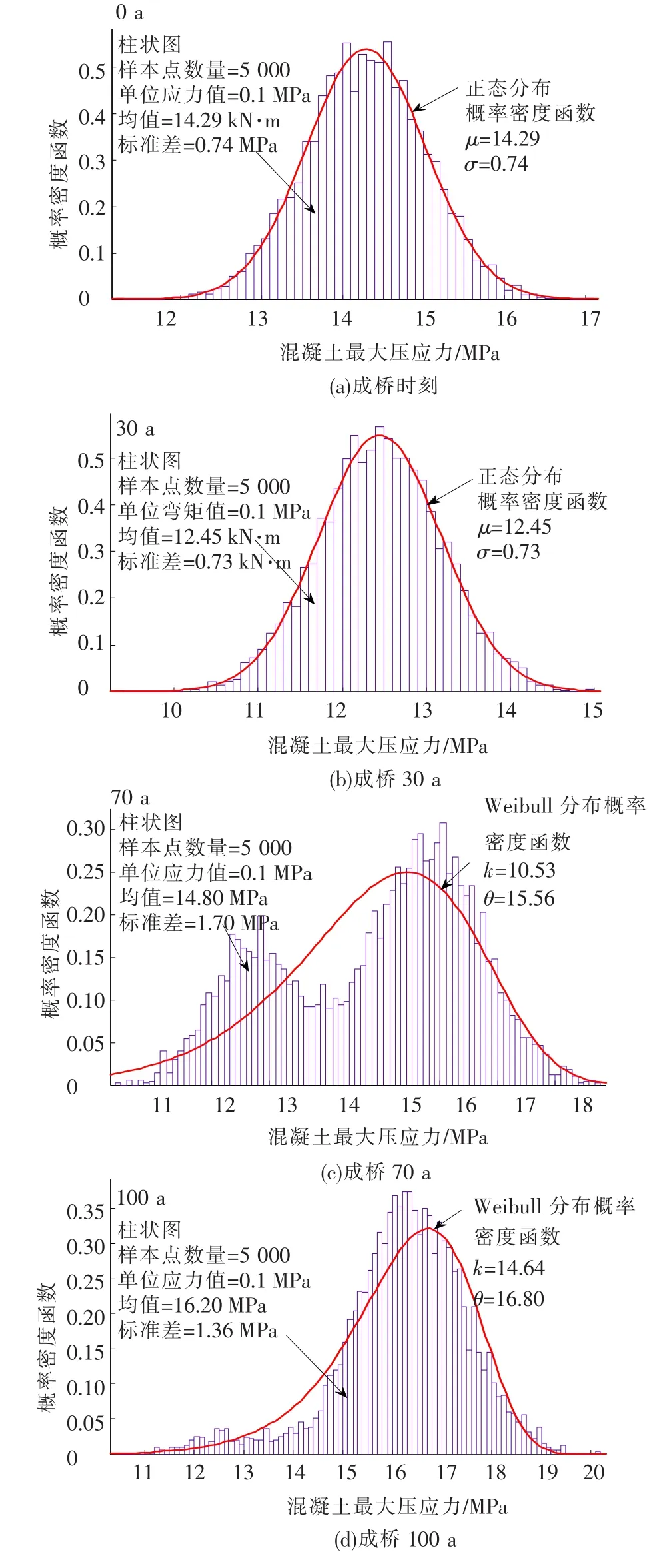
图9 构件4混凝土压应力的柱状图及其概率密度函数

图11给出了正常使用极限状态下关键构件和体系可靠度随时间的演变规律.与承载能力极限状态类似，在成桥初期最小构件拉应力可靠度βmin，2大于最小构件压应力可靠度 βmin，1，但在成桥15 a后前者开始小于后者.因此，结构的体系可靠度在成桥后15 a内由最小构件压应力可靠度决定而在剩余寿命期内将受最小构件拉应力可靠度控制.在寿命期内最小构件压应力可靠度始终出现在构件4，而最小构件拉应力可靠度则出现于3个不同的构件7，10和5(也就是中墩墩顶、中跨靠近中支点1/4跨径以及边跨靠近中支点1/4跨径位置).与承载能力极限状态不同，在成桥20 a内，由于混凝土徐变收缩作用最小构件压应力可靠度、最小构件拉应力可靠度以及正常使用极限状态下的体系可靠度均产生明显变化.此外，由于混凝土截面的削弱引起的混凝土应力增加从而导致体系可靠度由成桥时刻的2.0降低到成桥100 a时的－0.7，因此需要采取能够延缓混凝土截面开裂的加固措施.

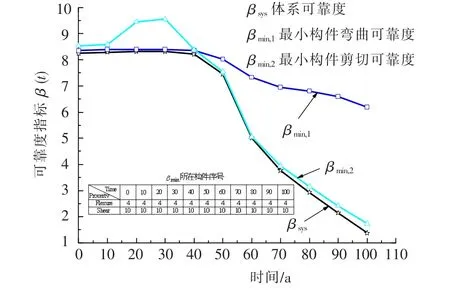
图10 承载能力极限状态关键构件和体系可靠度的演变过程

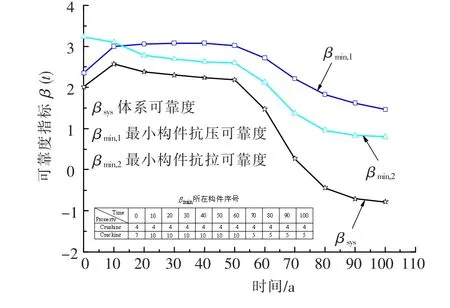
图11 正常使用极限状态关键构件和体系可靠度的演变过程

5 结论

1)同一混凝土截面中边缘之间的退化关键时刻差异明显，有些边缘上的钢筋在成桥20 a左右开始锈蚀，而有些则在寿命期内没有锈蚀，所以以混凝土边缘为基本单位模拟混凝土截面十分必要.

2)结构中不同构件的抗力和响应可能服从不同的分布类型，即使同一个构件在不同时间点其分布类型也可能不同.

3)承载能力极限状态下串联模型的体系可靠度在成桥后前40 a内由构件最小抗弯可靠度决定而在40 a后则受最小抗剪可靠度控制，正常使用极限状态下也出现类似的分析结果，说明不同的性能指标在寿命期内的演变规律差异明显，因此在体系可靠度分析中应包含尽量多的性能指标才可比较全面反映结构整体的性能演变规律.

4)最小构件抗剪可靠度不一定出现在最不利荷载效应位置，所以体系可靠度分析应包括结构中的所有构件而不仅仅是几个关键构件(如跨中截面的弯曲状态和支点截面的剪切状态).

5)模型梁中，由于混凝土截面腹板处箍筋大量损失引起结构抗剪能力的严重削弱，承载能力极限状态下的结构体系可靠度在成桥100 a时下降到1.2，因此需要采取能够提高结构抗剪承载能力的加固措施;正常使用极限状态下，由于混凝土截面的削弱引起的混凝土应力增加从而导致体系可靠度由成桥时刻的2.0降低到成桥100 a时的－0.7，因此需要采取能够延缓混凝土截面开裂的加固措施.

［1］ESTES A C，FRANGOPOL D M.Repair optimization of highway bridges using system reliability approach［J］.Journal of Structural Engineering，1999，125(7):766－775.

［2］ESTES A C，FRANGOPOL D M.Lifetime bridge maintenance strategies based on system reliability［J］.Structural Engineering International，1997，7(3):193 －198.

［3］AKGUL F，FRANGOPOL D M.Lifetime performance analysis of existing prestressed concrete bridge superstructures［J］.Journal of Structural Engineering，2004，130(12):1889－1903.

［4］AKGUL F，FRANGOPOL D M.Lifetime performance analysis of existing reinforced concrete bridgesⅠ:theory［J］.Journal of Infrastructure Systems，2005，11(2):122－128.

［5］AKGUL F，FRANGOPOL D M.Lifetime performance analysis of existing reinforced concrete bridges Π:application［J］.Journal of Infrastructure Systems，2005，11(2):129－141.

［6］THOFT-CHRISTENSEN P.Assessment of the reliability profiles for concrete bridges［J］.Engineering Structures，1998，20(11):1004 －1009.

［7］CECS 220:2007.混凝土结构耐久性评定标准［S］.北京:中国建筑工业出版社，2007:37－40.

［8］THOFT-CHRISTENSEN P.Stochastic modeling of the crack initiation time for reinforced concrete structures［C］//In Mohamed Elgaaly(eds).Advanced Technology in Structural Engineering Proc of Structures Congress.Philadelphia:ASCE，2000:1279－1286.

［9］李国平.桥梁结构分析综合系统［M］.上海:同济大学出版社，1998:16 －25.

［10］李国平.桥梁预应力混凝土技术及设计原理［M］.北京:人民交通出版社，2004:38－45.

［11］田浩.给定寿命期内混凝土桥梁性能演变分析［D］.上海:同济大学，2009.

［12］CHEN D，MAHADEVAN S.Chloride-induced reinforcement corrosion and concrete cracking simulation［J］.Cement and Concrete Composites，2008，30(3):227－238.

［13］LEE H S，NOGUCHI T，TOMOSAWA F.FEM analysis for structural performance of deteriorated RC structures due to rebar corrosion［C］//In Odd E，et al(eds).Concrete under Severe Conditions 2:Environment and loading Proc of the Second International Conference.Tromso:The Norwegian University of Science and Technology，1998:327－336.

［14］JUNG W Y，YOON Y S，SOHN Y M.Predicting the remaining service life of land concrete by steel corrosion［J］.Cement and Concrete Research，2003，33(5):663－677.

［15］DARMAWAN M S，STEWART M G.Spatial time dependent reliability analysis of corroding pretensioned prestressed concrete bridge girders［J］.Structural Safety，2007，29(1):16－31.

［16］DARMAWAN M S，STEWART M G.Effect of pitting corrosion on capacity of prestressing wires［J］.Magazine of Concrete Research，2007，59(2):131－139.

［17］NOWAK A S.Reliability of structures［M］.New York:McGraw-Hill Company，2000.

［18］ESTES A C，FRANGOPOL D M.RELSYS:a computer program for structural system reliability analysis［J］.Structure Engineering ＆ Mechanics，1998，6(8):901－919.

System reliability analysis of prestressed concrete continuous bridges in service life

TIAN Hao1，2，CHEN Ai-rong1

(1.Department of Bridge Engineering，Tongji University，200092 Shanghai，China，tianhao－8@163.com;2.Zhejiang Scientific Research Institute of Communication，310006 Hangzhou，China)

To evaluate the lifetime performance of prestressed concrete bridges exposed to chloride penetration environment，a probabilistic and finite element-based lifetime performance assessment approach for prestressed concrete bridges is proposed.Firstly，three critical times in the degradation process are discussed and their computing formulas are presented.Secondly，an analysis program named CBDAS(Concrete Bridge Durability Analysis System)is written based on the numerical simulation methods with respect to the deterioration of materials’mechanical properties，reduction of sectional areas and variation of overall structural mechanics performance.Finally，the assessment method for calculating time-variant system reliability of prestressed concrete bridges is proposed associated with the analysis program CBDAS，Monte-Carlo simulation and analysis technique of the system reliability.The lifetime performance of a prestressed concrete continuous bridge under chloride penetration-induced corrosion is investigated by using the time-variant system reliability.

prestressed concrete bridge;service life;lifetime performance;Monte-Carlo simulations;timevariant system reliability

TU375.4

A

0367－6234(2011)10－0105－08

2010－05－09.

国家高技术研究发展计划(2007AA11Z104);西部交通建设科技项目(2006 318 223 02－01).

田 浩(1982—)，男，博士;

陈艾荣(1963—)，男，教授，博士生导师.

(编辑 赵丽莹)