基于复合分类器的网络入侵检测模型
刘克文,张贲,王宇飞
(1.中国电力科学研究院,北京市,100192;2.华北电网有限公司,北京市,100053;3.华北电力大学控制与计算机工程学院,北京市,102206)
0 引言
随着信息技术和互联网的飞速发展,国家电网公司的信息化水平日益提高,信息系统也已渗透到整个公司的生产、经营、管理等各环节,并支撑了国家电网公司各项业务开展。但随着公司网络规模的扩大,网络信息安全问题日益突显,入侵检测作为网络信息安全的基础性研究逐渐引起研究人员关注。入侵检测是对入侵行为的检测,入侵检测系统通过收集网络及计算机系统内所有关键节点的信息,检查网络或系统中是否存在违反安全策略行为及被攻击迹象。因而设计高效、准确的入侵检测模型,现实意义重大。
解决入侵检测问题的思路一般是将入侵检测问题抽象成一个复杂的多分类问题,通过构造分类器来实现对入侵检测的判别。常用的入侵检测算法有:核主成分分析(kernel principal component analysis,KPCA)结合前馈(back propagation,BP)神经网络构造分类器[1];KPCA结合支持向量机(support vector machine,SVM)构造分类器[2-3];粒子群算法(particle swarm optimization,PSO)优化权重矩阵和阈值的BPNN构造分类器[4];主 成 分 分 析 (principal component analysis,PCA)、线性判别分析 (linear discriminant analysis,LDA)和 K-最近邻居法 (knearest neighbor,KNN)构造分类器[5];PCA、KPCA等方法构造分类器[6]。上述常用入侵检测算法中存在数据冗余高、分类精度低、运算时间长和迭代次数多等问题。为更好地解决上述问题,本文设计了一种基于复合分类器的入侵检测模型。复合分类器由KPCA、BP神经网络和量子遗传算法(quantum genetic algorithm,QGA)组合而成。复合分类器通过对原始数据降维并优化分类器参数的方式完成大量样本的训练、分类模型生成,再使用分类模型对待测样本做出准确分类,最后通过实验证明了基于复合分类器的入侵检测模型的有效性。
1 复合分类器
1.1 KPCA 算法
KPCA是一种高效的非线性特征选择算法,适用于高维原始数据的主成分分析,即原始数据降维处理。KPCA改进自线性的PCA[7],KPCA的核心思想是将原n维欧氏空间Rn的数据通过核函数映射到Hilbert特征空间,在Hilbert空间作线性PCA。KPCA算法流程为:先引入从空间Rn到Hilbert空间的变换x=Φ(xi),并认为Φ(xi)已经中心化,计算Hilbert空间中各点的协方差矩阵C
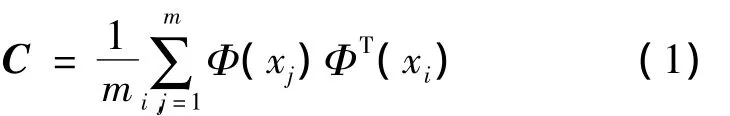
式中:m代表Hilbert空间维数。
设C的特征值为λ及非零特征值对应的特征向量为υ,可证明υ一定处于由Φ(x1),…,Φ(xm)构成的空间中,则υ可表示为
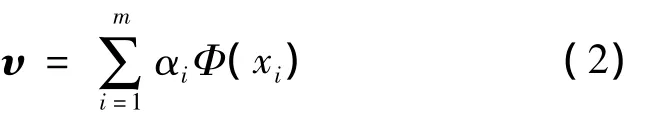
此时原问题变为求解αi,则有
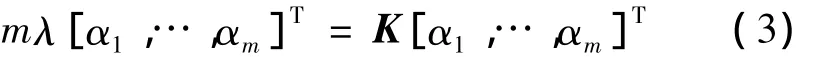
式中:K代表Φ(xi)和Φ(xj)的内积,Kij=<Φ(xi),Φ(xj)> 是 Gram 矩阵。令 λn<αn,αn>=1,即 λn正交化,计算各Φ(xi)在υ上的投影gi(x),其中gi(x)是对应于Φ(xi)的非线性主成分分量,
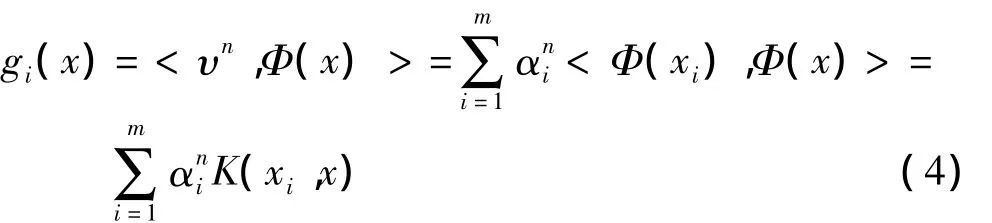
则g(x)=[g1(x),…,gn(x)]T为样本的特征向量。比值 λ表示了分量gi(x)对样本总体方差的贡献度,最终选取若干个最大的特征值对应的特征向量υi构成实验所需的特征子空间。
1.2 BP 神经网络
BP神经网络是一种典型的前馈网络,通过网络结构正向传递计算结果、使用训练函数反向修正网络权重矩阵和阈值,完成样本的训练模型的构造,再使用构造好的训练模型完成对待测样本处理[8]。
下面几个参数决定了BP神经网络最终精度:隐含层数目、每层神经元个数、训练函数、学习函数、传递函数、权重矩阵和阈值。其中,除权重矩阵和阈值以外的其他参数均根据实际问题设定,而权重矩阵和阈值一般选[0,1]之间随机数[9]。
1.3 QGA 算法
QGA是遗传算法和量子计算相结合的算法[10]。与普通遗传算法相比,QGA的特点是使用量子位编码来表示染色体,并通过量子旋转门和染色体交叉来完成种群进化,因而QGA种群规模更小,且收敛速度快,抗早熟能力强。
QGA中的染色体用量子位来描述,即随机概率的方式。1个量子位既可以表示0或者1两种状态,又可以表示0、1之间的任意中间态。设有m个量子位,则可以有2m种状态,所以QGA的种群规模远小于普通遗传算法(genetic algorithm,GA)。设a、b分别为状态|0〉和|1〉的概率幅,在满足|a|2+|b|2=1的情况下,则[0,1]之间任意量子状态可表示为
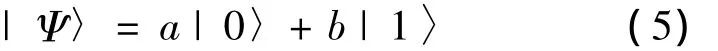
即状态Ψ为状态|0〉和|1〉的叠加。
在QGA中进化过程是由量子门旋转和染色体交叉共同作用完成。量子门公式(6)中θ是旋转角,U是量子门旋转矩阵,公式(7)是量子位更新公式,
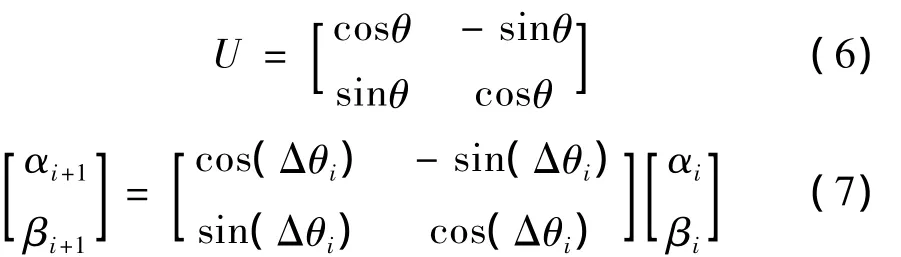
公式(7)中Δθi的大小直接决定了算法收敛速度,Δθi取值太小算法收敛很慢,Δθi取值太大种群易早熟,通常 Δθi∈[0.001π,0.005π]。染色体交叉的作用是防止种群早熟,通常采用全干扰交叉操作[11]。
2 基于复合分类器的入侵检测模型设计
2.1 复合分类器模块结构
复合分类器由KPCA模块、BP神经网络模块和QGA模块组成。其中KPCA模块负责原始样本数据降维处理,QGA模块负责向BP神经网络传递训练参数并计算适应度函数Fitness,由BP神经网络模块完成最后的数据训练、分类,具体结构见图1。
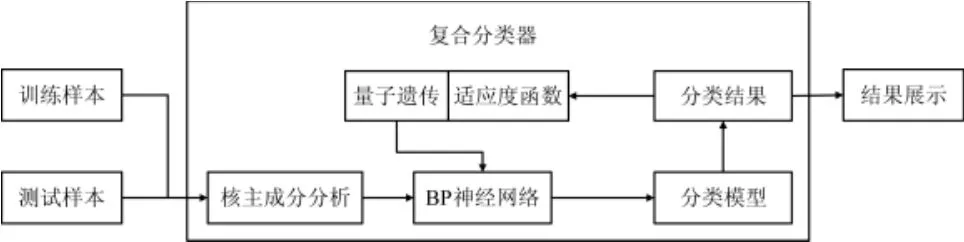
图1 复合分类器结构Fig.1 Construction of hybrid classifier
2.2 复合分类器模块设计
2.2.1 KPCA 模块设计
通常用于入侵检测的原始数据均来自入侵检测系统等网络安全设备的日志,并且国家电网公司由于所属各机构具体使用的网络安全设备品牌、功能各异,因而需要对各子机构上报的日志做融合处理,即合并各类日志的不同数据字段。所以入侵检测模型需要处理、分析的原始数据具有数据量大、维数高等特点,通常合并后的日志文件都以MB,甚至GB为存储单位,并且日志中每条记录的维数都有几十维,甚至上百维。因而在针对入侵检测问题设计复合分类器时,首要考虑的是对原始数据做降维处理,又因为每条记录中不同维度之间常常是复杂的非线性关系,所以复合分类器使用KPCA做降维工具,具体选用Gauss径向基函数作为KPCA核函数
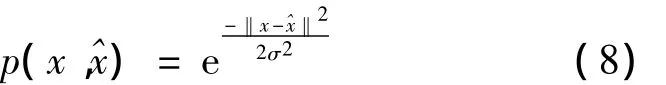
2.2.2 BP 神经网络模块设计
复合分类器选用2层BP神经网络。设原始IDS的n维数据经KPCA降维后得到m维新数据样本,则在BP神经网络中选用m维数据做为BP神经网络的输入数据,即BP神经网络输入层有m个神经元。又因为待求解问题为分类问题,所以BP神经网络的输出层是1个神经元。BP神经网络的隐层神经元个数为
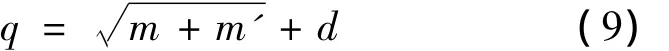
式中:m、m′分别是输入层、输出层神经元个数,d是[1,10]之间的随机整数。BP神经网络中传递函数均采用S型函数tansig。权重矩阵和阈值由QGA迭代给出。
2.2.3 适应度函数
设测试样本的总体分类准确率为Θ,则PSO的适应度函数为

适应度函数的阈值为Fθ,当F(i)<Fθ时,迭代结束。Fθ=1.0152 时,Θ =0.985。
3 实验研究
为充分证明本文基于复合分类器的入侵检测模型的有效性,设计2组实验分别就入侵检测模型的准确率和泛化能力给予验证。其中:实验一主要为验证本文入侵检测模型在国家电网网络安全告警中的实用性;实验二主要为验证本文入侵检测模型的泛化能力,并且与当前常用入侵检测算法进行性能横向比较。
3.1 实验1
选用连续100天的网络安全日志构成实验样本,其中每条样本的检测时间间隔为1 s,并且每条样本由72维数据字段构成,其中2个特定字段分别定义了网络攻击大类和具体攻击子类其余70个字段分别表示记录的不同特征。其中日志共包含5大类告警,分别为“恶意软件类”、“网络攻击类”、“信息破坏类”、“信息内容安全类”和“其他告警”等。连续100天的日志共有8226217条记录,从中随机抽取10%的原始数据822622条做实验数据,并从实验数据中随机抽取70%的数据575835条做训练样本,其余30%的数据246787条做测试样本,再随机抽取10%的数据82262条用于KPCA降维,详细样本抽取情况如表1所示。
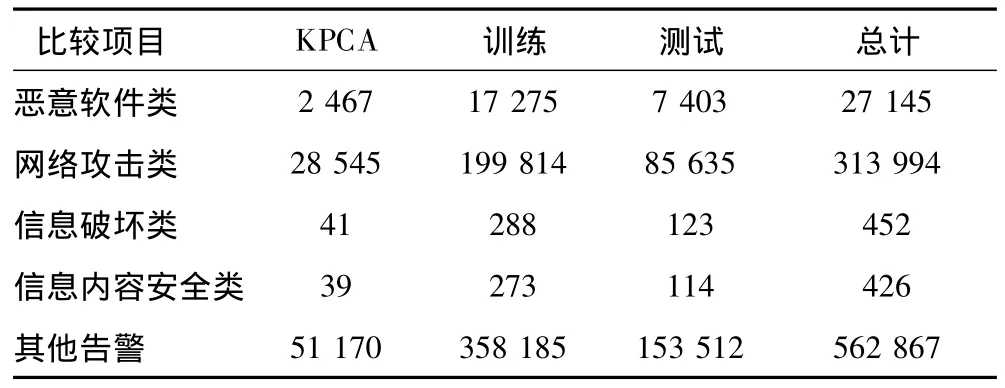
表1 实验1样本Tab.1 No.1 experimental samples
在确定实验样本后,需对原始实验样本做降维处理。对原始样本记录中除表示入侵分类的2个特殊字段以外的70维字段用KPCA做降维处理,KPCA核函数参数取10,得到70维特征对应的λi。取其中λi最大的前10项构成新数据样本,每项的λi如表2所示,可以根据算出新样本分量(x)对样本总体方差的贡献度大于85%。
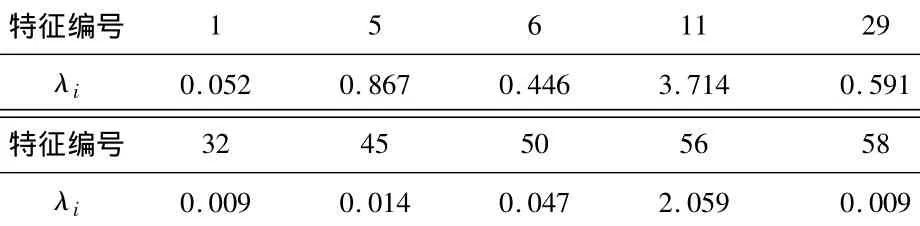
表2 KPCA计算结果(实验1)Tab.2 Results of KPCA algorithm for No.1 experiment
将KPCA降维后的训练样本送入BP神经网络,得到训练模型,训练模型权重矩阵和阈值由QGA迭代得到,QGA最大迭代次数1500,BP神经网络训练次数10000,实验结果见表3。设某一类样本是正样本,则其他类别样本统称为负样本,可得漏报率(正样本出错个数/正样本总数)和误报率(负样本出错个数/负样本总数)。
由表3可知,国家电网实验样本最终的分类正确率达到98.5002%,与入侵检测模型设定的收敛阈值0.985非常接近,但对于小类别样本的误报率和漏报率偏高。其原因在于:(1)因为实验样本采集自真实公司网络环境,因此数据坏点和噪声不可避免;(2)使用KPCA降维虽然大大减少了实验运算量,但也忽略了部分影响因素(略去的60维数据);(3)神经网络对于小类别样本的不敏感性也造成了较高的漏报率和误报率。但从入侵检测整体上衡量实验一的结果,其入侵检测模型可信度较高,能达到事先设定的期望值0.985。
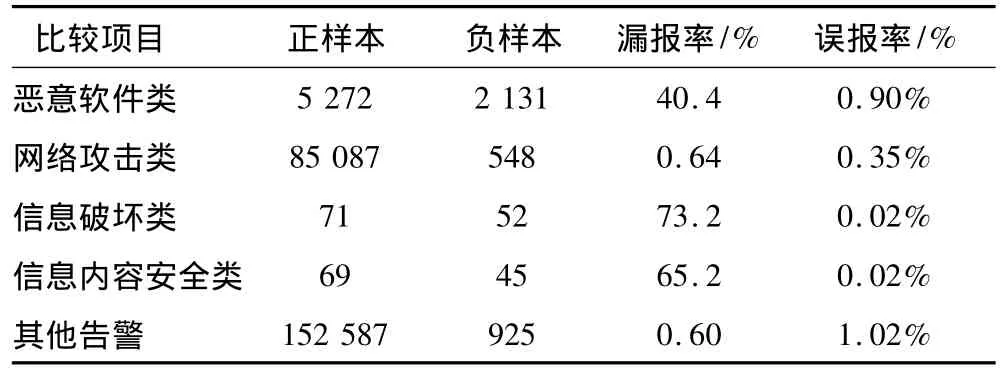
表3 QGA&BPNN实验结果(实验1)Tab.3 Results of QGA & BPNN for No.1 experiment
3.2 实验2
选用 KDDCUP99数据集[12]做实验数据,KDDCUP99数据集中将样本数据分为Normal(正常)、DoS(拒绝服务)、R2L(远程主机的未授权访问)、U2R(未授权的本地超级用户特权访问)、Probe(端口扫描)等。因 KDDCUP99原始数据接近5000000条,为方便实验本文在保持原始数据类别比例结构不变情况下,随机抽取10%的原始数据494021条做实验数据,并从实验数据中随机抽取70%的数据345815条做训练样本,其余30%的数据148206条做测试样本,再随机抽取10%的数据49405条用于KPCA降维,详细样本抽取情况如表4所示。
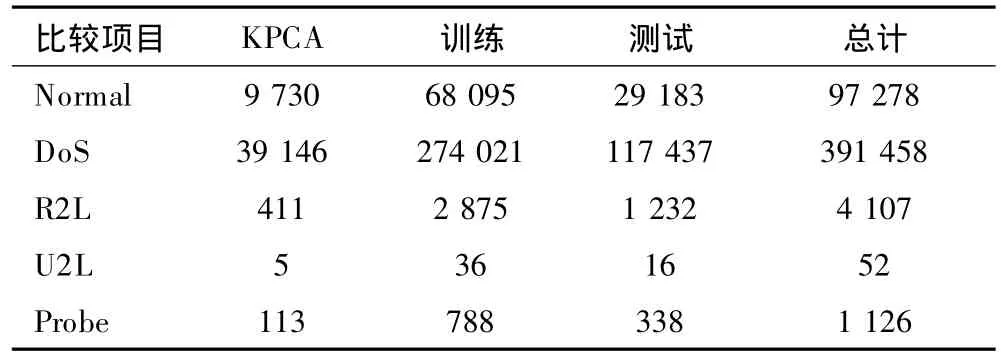
表4 实验样本(实验2)Tab.4 No.2 experimental samples
在确定实验样本后,需对原始实验样本做数据结构分析处理,即降维处理。KDDCUP99原始数据有42维,其中前41维是样本特征,最后1维是样本的分类,因此对样本前41维用KPCA做降维处理,KPCA核函数参数取80,得到41维特征对应的λi。其中前10维的λi也是41个λi中值最大的10项,如表5所示,其他31维的 λi取值范围均在[9.51×10-8,2.65 ×10-4],所以取 λi最大的前10 项特征构成新样本,根据算出新样本分量对样本总体方差的贡献度大于96%。
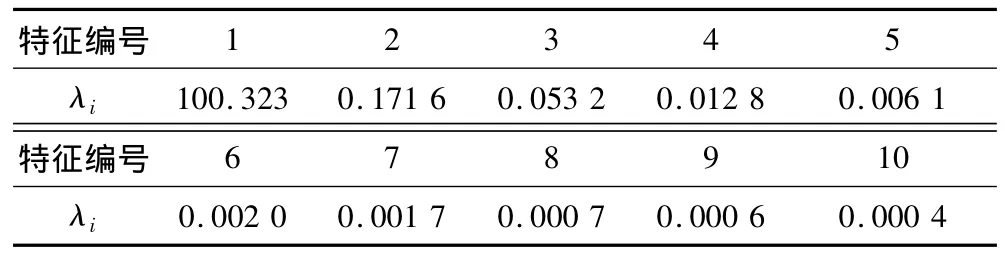
表5 KPCA计算结果(实验2)Tab.5 Results of KPCA algorithm for No.2 experiment
将KPCA降维后的训练样本送入BPNN,得到训练模型,训练模型权重矩阵和阈值由QGA迭代得到,QGA最大迭代次数2000,BPNN训练次数15000。QGA的Fitness曲线见图2。从图2可知,在第400代左右适应度函数基本趋于稳定,最终在第810代收敛于Fθ,即总体分类正确率不小于0.985,实验结果见表6。
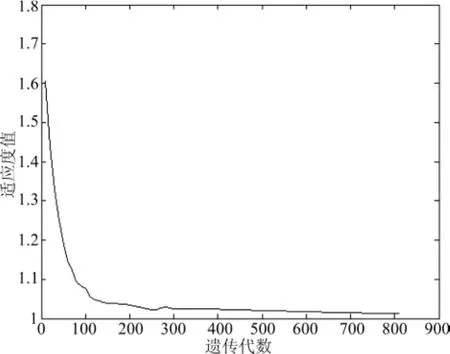
图2 适应度函数曲线Fig.2 Curve of fitness function
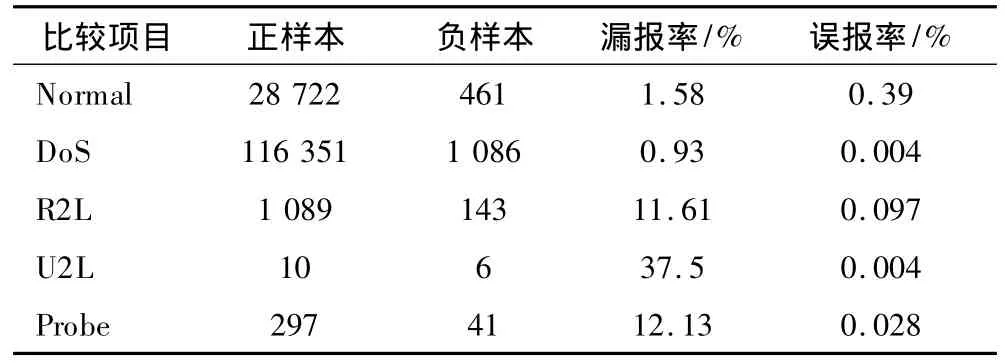
表6 QGA&BPNN实验结果(实验2)Tab.6 Results of QGA & BPNN for No.2 experiment
横坐标为进化代数(0,100,200,),纵坐标为适应度函数,为进一步体现本文入侵检测模型的算法优势,现选取 KPCA 结合 BP 方法[1]、SVM 方法[2]、PSO结合BP方法[4]做横向比较,结果见表7。
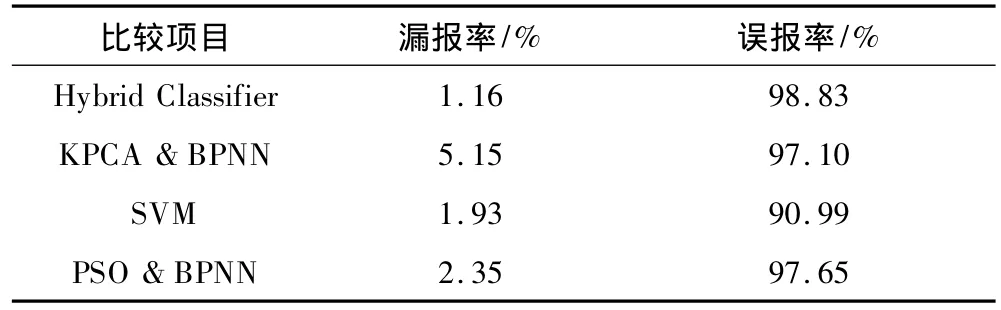
表7 实验结果比较Tab.7 Comparison of experimental results
由表7可知,其他分类算法在准确度上并不理想,特别是FPR偏高。其原因为:文献[1]使用未经参数优化的BPNN做分类器,因而不可避免神经网络易陷于局部极小点、权重和阈值选取困难等固有弱点;文献[2]没有使用群智能优化算法为SVM寻参,因而造成训练模型精度低;文献[4]没有对原始数据降维,所以算法分类时间远高于其他分类算法,并且PSO的局部寻优能力不如QGA,因而误差较大。
4 结论
本文设计了一种由KPCA、BPNN和QGA 3种人工智能算法组合而成的入侵检测模型,克服了原有入侵检测算法中普遍存在的数据维数高、分类器参数选取困难、分类器准确率低等问题。相比于其他常见入侵检测算法,本文的基于复合分类器的入侵检测模型在分类准确率方面优势明显。又因本文实验数据集随机抽取自海量原始样本,并且训练样本集和测试样本集不存在交集,即完全独立,从而保证了100%开集分类测试,所以复合分类器的泛化能力得到保证。最后通过实验证明了复合分类器的有效性。
[1]刘完芳,黄生叶,常卫东.基于KPCA入侵检测特征提取技术[J].微计算机信息,2007,13(9):81-83.
[2]Bao P Q,Yang M F.Intrusion detection based on KCPA and SVM[J].Computer Applications and Software,2006,23(2):125-127.
[3]Sun Z B,Sun M S.A Multi-classification intrusion detection system based on KPCA and SVM[J].Information Technology,2007,7(11):29-31.
[4] Lin Z M,Chen G L,Guo W L,et al.PSO-BPNN-based prediction of network security situation[C]//The 3rd International Conference on Innovative Computing Information and Control.Fuzhou,China:IEEE,2008:37-41.
[5] Zhang R X,Wang Y.Fusion of PCA and LDA for intrusion detection[J].Computer Technology and Development,2009,19(11):132-135.
[6]Gao H H,Yang H H,Wang X Y.PCA/KPCA feature extraction approach to SVM for anomaly detection[J].Journal of East China University of Science and Technology:Natural Science Edition,2006,32(3):321-326.
[7] Martinez A M,Kaka A C.PCA versus LDA[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2001,23(2):228-233.
[8] Bilski J,Rutkowski L.A fast training algorithm for neural networks[J].IEEE Trans on Circuits and System II:Analog and Digital Signal Processing,1998,45(6):749-753.
[9] Purucker M C.Neural network quarterbacking[J].IEEE Potentials,1996,15(3):9-15.
[10] Li B B,Wang L.A hybrid quantum-inspired genetic algorithm for multiobjective flow shop scheduling[J].IEEE Trans on Systems,Man,and Cybernetics,Part B:Cybernetics,2007,37(3):576-591.
[11] Narayanan A,Moore M.Quantum-inspired genetic algorithm[C]//Proc.of IEEE International Conference on Evolutionary Computation.Piscataway,USA:IEEE,1996:279-294.
[12] Hettich S,Bay S D.KDD cup 99 task description[EB/OL].http://kdd.ics.uci.edu/databases/kddcup 99/task.html.1999.

