罗兰C系统非时基交叉圆定位方法研究＊

刘敬虎 朱银兵 李 豹

（91576部队1） 宁波 315021）（海军工程大学电气与信息工程学院2） 武汉 430033）

1 引言

罗兰C系统通常采用双曲线测时差法定位，即在某一位置接收同一罗兰C台链的主台和两个副台信号，测量接收到的两个副台相对主台的时差，利用双曲线定位原理解算船位。该方法采用单台链定位，定位精度受台站布设方式的限制，最佳定位区位于正基线一侧扇形区域。为了实现罗兰C信号覆盖区的有效定位，增加台站布设灵活性，发挥罗兰C台链的定位潜力，丁佳波对单台链定位的奇异现象进行了分析，提出了利用高斯等角球面改正算法计算船位［1］，分析了台址位移对双曲线大地坐标的影响及罗兰C负区定位的计算方法［2］；此外，一些学者利用纬度归化处理方法［3］对罗兰C信号的多台链定位进行了深入研究［4～9］，并对罗兰C的非时基圆圆定位算法进行了初步分析［10］。其中非时基圆圆定位算法能够解决单台链双曲线定位中基线延长线附近出现奇异现象这一问题，有效提高定位精度。因此，本文将详细推导罗兰C系统的非时基交叉圆定位方法，并结合试验与单台链双曲线定位算法进行对比，分析算法的定位精度。

2 罗兰C系统交叉圆定位原理

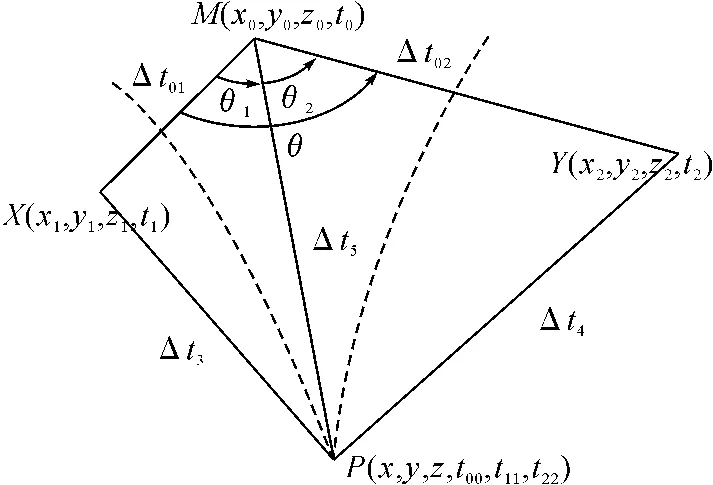
图1 交叉圆定位示意图

在直角坐标系中，地球表面任意一点可用三维坐标（x，y，z）表示，如果能够求解出船位相对主台与两个副台的球面半径Rm、Rs1与Rs2，则由以主台与两个副台为球面中心，分别以Rm、Rs1与Rs2为半径的球面和大地球面相交即可求解出船位，交叉圆定位正是利用该原理实现船位解算的［6］。

如图1所示，假设主台M与副台X、Y的直角坐标分别为（x0，y0，z0）、（x1，y1，z1）与（x2，y2，z2），船位为P（x，y，z）。则有：

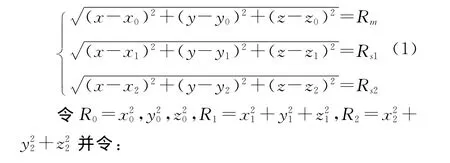
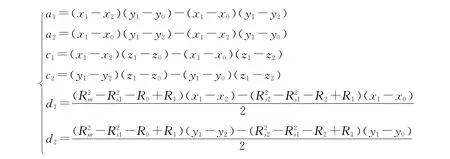
则方程（1）可简化为：

联立方程（1）、（2）可得：

其中，

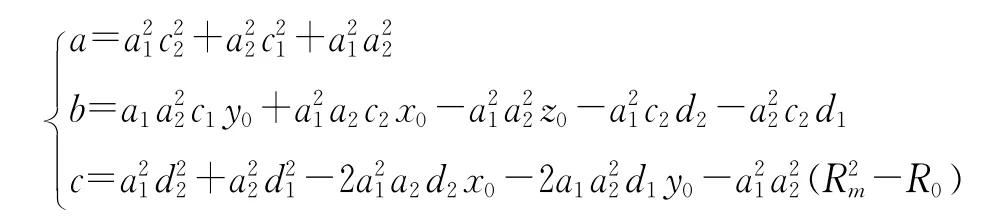
由此可得：

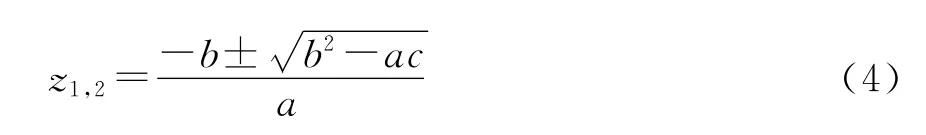
由于南半球没有布设罗兰C台链，因此z必须满足条件z≥0，故可以剔除其中不满足条件的解，至此完成概位解算。如果得到的概位有多个，需要根据实际情况选择最为可能的概位，然后由此概位利用时差与船位的函数关系进行牛顿迭代运算以得到精确船位。

3 罗兰C系统交叉圆定位方法推导

由上述定位原理推导可知，船位相对主台与两个副台的球面半径Rm、Rs1与Rs2的求解是实现罗兰C系统交叉圆定位的关键所在。以往认为，要精确求解船位相对主副台的时间差Δt，就要求接收机与发射台在时间上严格同步，但在工程实现中时间对准难度大，而且成本昂贵。为此，本文将在现有罗兰C基础上，详细推导船位相对主台与两个副台球面半径Rm、Rs1与Rs2的计算方法，以实现罗兰C系统的交叉圆定位。

如图1所示，以t0表示主台M发送导航信息时刻，t1表示副台X收到主台信号时刻，t2表示副台Y收到主台信号时刻，t22表示船位P收到主台信号时刻，t00表示船位P收到由主台信号发射到副台X然后经过转发的信号时刻，t11表示船位P收到由主台信号发射到副台Y然后经过转发的信号时刻，Δt01表示主台信号到达副台X所消耗的时间，Δt02表示主台信号到达副台Y所消耗的时间，单位均为μs。由于Δt01、Δt02及θ角可以事先精确测量得到，t00、t11、t22可以由罗兰 C接收机即时精确测量，c为电波传播速度，则根据球面三角形关系有如下方程组：

方程组（5）中，Δt01c、Δt02c、Δt3c、Δt4c及Δt5c均以弧度表示；δt1、δt2分别表示副台X、Y的发射延迟，可事先测量。因此，式（5）中有θ1、θ2、t0、Δt3、Δt4、Δt5等6个未知数，通过求解Δt3、Δt4、Δt5即可确定三个圆的半径，即可实现船位的确定。

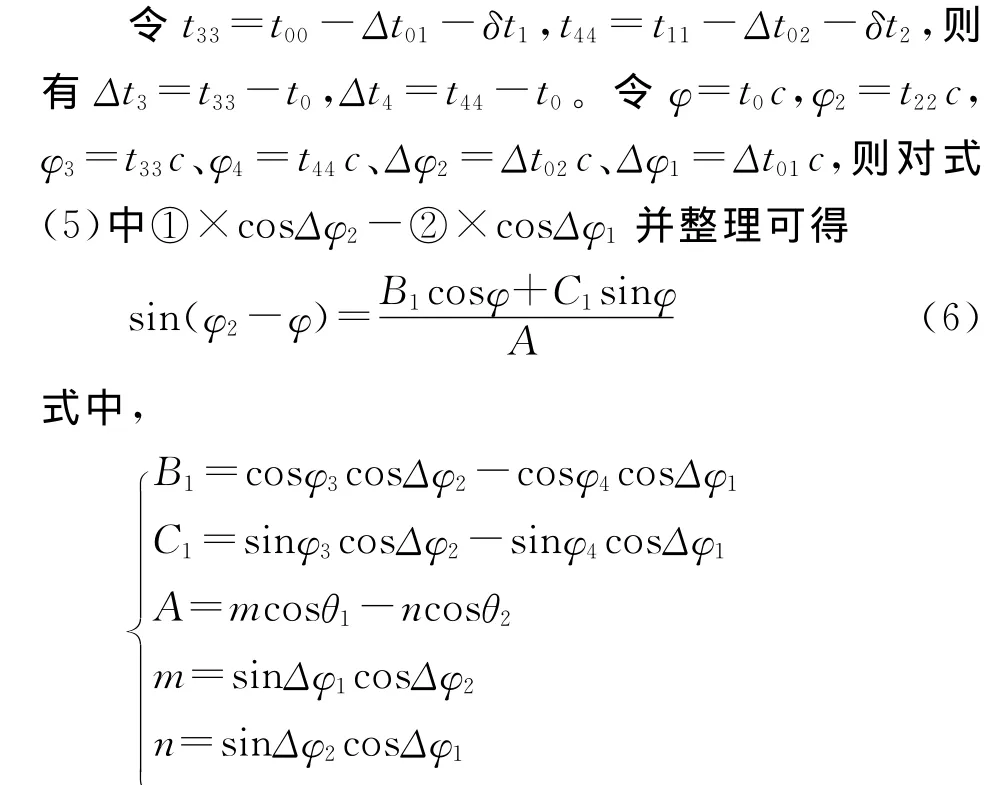
展开式（6）有

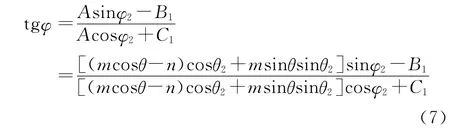
同理，式（5）中①×sinΔφ2cosθ2－②×sinΔφ1 cosθ1有

展开式（8）有

联立式（7）与式（9）可得：

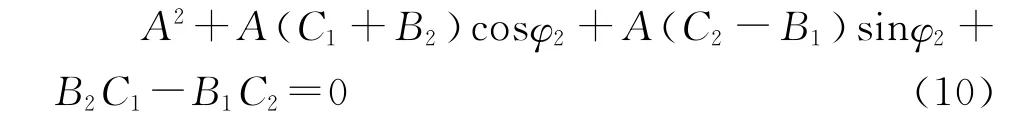
由于B2C1－B1C2＝Asin（φ4－φ3），方程（10）

可进一步简化为

对方程（11）进行求解，当A＝0时有

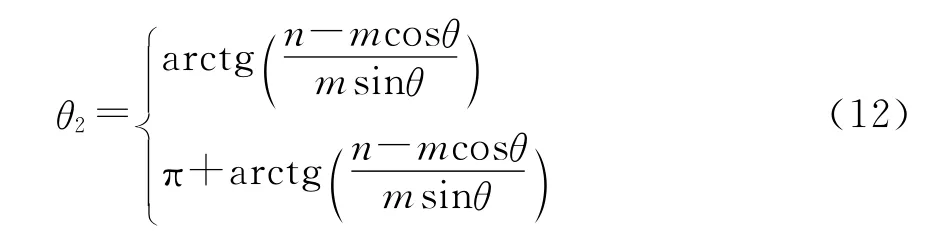
当A≠0时有

由于

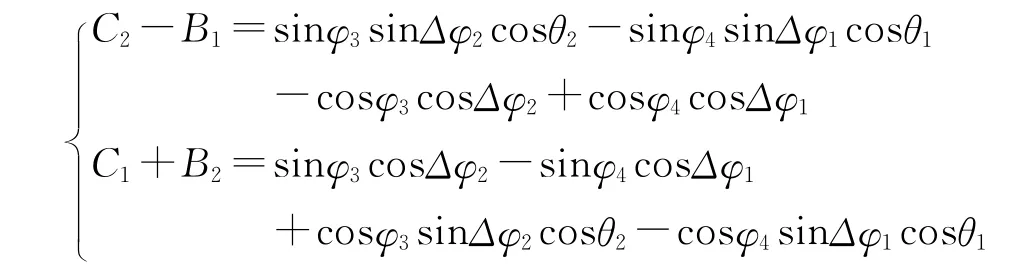
式（13）可简化为

由式（12）、式（16）可知，方程组（5）的解最多有6个，但实际中满足条件的只有一个。因此，需要考虑解的实际意义：θ2为实根，且0≤θ2≤π剔除不满足条件的解。对于满足条件的解，可根据式（7）解出主台发射时刻t0，t0必须满足以下条件：1）t0≥0；2）t22－t0≥0，由此可进一步剔除不满足条件的解，得到主副台信号到船位的传播时间Δt3、Δt4、Δt5，从而求解出船位相对主台与两个副台球面半径Rm、Rs1与Rs2。

4 牛顿迭代求解

假设利用上述定位原理与推导过程得到的概位为（φc，λc），为了求解精确船位（φ，λ），采用牛顿迭代算法处理。假设船位与副台2基线的夹角为θ，则θ及时差ξ可视为未知船位（φ，λ）的二元连续函数，于是有

对式（17）两边求导可得

由于θ，θc，ξ，ξc都是已知的，只要求出四个偏导数在概位的取值，就可以求出误差Δφ和Δλ的近似值。假设A1、A2是辅助球面上概位到岸台的方位角，则有：

迭代计算过程如下：首先以新的概位替换原来概位，即：φc＋Δφ⇒φc，λc＋Δλ⇒λc；然后重新计算式（18）～式（20），得到新的φc、λc及新的方程组，直到｜Δφ｜＜ε且｜Δλ｜＜ε。其中，ε为预先给定的收敛门限ε＝10－7rad。

5 算法性能分析

为了分析交叉圆定位算法的精度，笔者多次利用XN-800接收机及海格通信公司样机接收实际罗兰C信号，并利用NI公司采集卡PXI-5922采集接收机射频端信号，然后对信号进行处理与定位解算，并与接收机时差测量及定位结果进行比较。相关信号采集试验现场如图2所示。

图2 试验现场

由于定位算法中的部分参数设定与附加二次相位因子ASF修正模型目前不完全统一，同一时差在不同算法下的定位结果不完全相同。因此，本文在分析定位精度时不考虑ASF的影响，主要参考指标为时差测量结果，并以GPS定位结果为参照，与单台链双曲线定位算法进行对比分析。测量点 GPS定位结果为 N30°34′55″，E114°14′23.88″，多次试验结果表明测量点8390台链实际测量时差为TD1＝14988.5μs，TD2＝33427μs；6780台链实际测量时差为 TD1＝14565μs，TD2＝28120μs，采用上述非时基交叉圆定位及单台链双曲线定位算法得到的试验结果如表1所示。

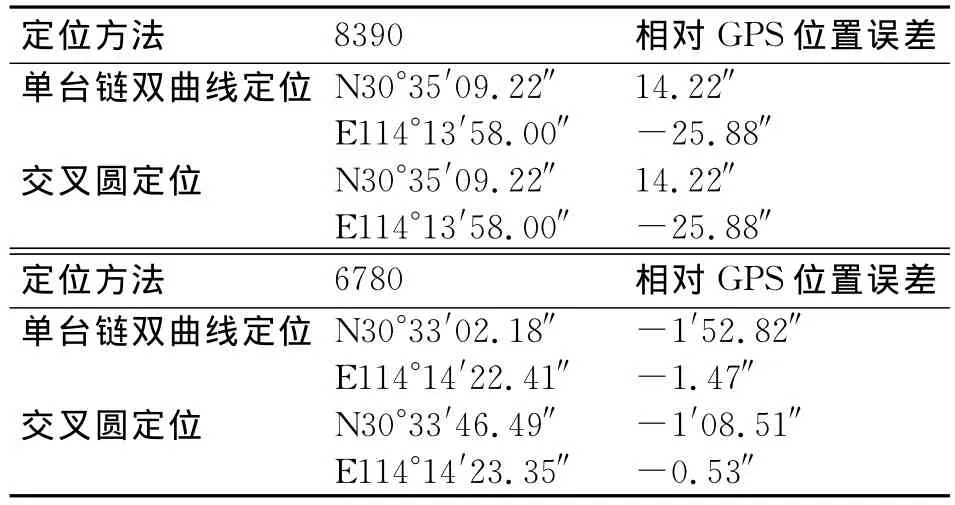
表1 交叉圆定位试验对比结果

由表1可见，由于测量点相对于8390台链的几何因子GDOP较好，采用单台链双曲线定位与交叉圆定位方法得到的定位结果一致；而对于6780台链，由于GDOP相对较差，采用交叉圆定位方法得到的定位结果优于采用单台链双曲线定位算法得到的结果。即在几何因子GDOP不断变差的过程中，交叉圆定位方法的定位结果优于单台链双曲线定位算法的结果。因此，在基线延长线附近，交叉圆定位方法的定位结果也必然由优于单台链双曲线定位算法的定位结果。

由此可见，采用交叉圆定位方法的定位结果不劣于单台链双曲线定位算法的定位结果，而且，采用交叉圆定位方法能够有效解决单台链双曲线定位算法在基线延长线附近定位时存在“奇异”现象这一问题，有效扩大罗兰C系统的作用区域，提高系统定位精度。

6 结语

本文在分析罗兰C系统非时基交叉圆定位原理基础上，详细推导了罗兰C非时基交叉圆定位算法及其迭代算法，然后通过试验的方法得到了测量点相对不同台链的时差测量结果。根据该时差测量结果进行了单台链双曲线定位与非时基交叉圆定位算法比较。结果表明：在几何因子GDOP较好的位置，交叉圆定位方法的定位结果与单台链双曲线定位算法的定位结果相差不大，但在GDOP较差的位置，交叉圆定位方法的定位结果明显优于单台链双曲线定位算法的定位结果；采用交叉圆定位方法能够有效解决单台链双曲线定位方法在基线延长线附近定位时存在“奇异”现象这一问题等主要结论。所述非时基交叉圆定位方法对扩展罗兰C系统有效覆盖区域，提高罗兰C系统定位精度具有一定实际意义。

［1］丁佳波.罗兰C系统导航定位计算中的奇异现象及分析研究［J］.导航，1999，35（1）：100～106

［2］丁佳波.台址位移对双曲线大地坐标的影响及罗兰C负区计算［J］.导航，1994，30（2）：96～102

［3］G.W.A.Ofermans，D.van Willigen，A.W.S.Helwig，et al.An European navigation solution［C］／／Proc.of the 29th Annual Technical Symposium of the International Loran Association，Paris，November，2000：649～661

［4］秦卫华，杨致友.多台链罗兰C信号搜索方法研究［J］.导航，1996，32（2）：53～58

［5］丁佳波.关于不同台链组合双曲线导航系统的定位计算［J］.导航，1994，30（4）：70～77

［6］袁小利，高锐.罗兰C多台链定位解算技术及其应用［J］.导航，2002，38（1）：96～100

［7］闵思鹤，王甲池，江太辉，等.基于双台链罗兰C导航仪的双曲线导航定位算法［J］.电子与信息学报，2003，25（5）：700～703

［8］闵思鹤，王甲池，江太辉，等.基于双台链罗兰C导航定位新算法［J］.无线电通信技术，2002，28（4）：10～12

［9］曹可劲，朱银兵，张磊，等.罗兰C双台链交叉定位算法研究［J］.海军工程大学学报，2011，23（3）：1～4

［10］祝子明.对罗兰C系统进行非时基圆定位方法的初步研究［J］.导航，2006，42（4）：103～107.