基于UDEC的某公路顺层边坡优化设计研究

张贵庆

(山西省水利水电勘测设计研究院,山西 太原 030024)

1 概述

随着全国工程建设规模不断扩大,岩石边坡特别是复杂地质条件下的岩石高边坡问题就成为一个热点和难点问题[1]。

岩体中的结构面是降低岩体的强度和产生大变形的主要因素,尤其是缓倾角的结构面和软弱夹层对岩体的稳定性起着绝对控制作用[2]。结构面按其成因以及规模特点大致可分为断层、层面、节理及裂隙等,对于天然的或人工开挖形成的边坡,其变形特点和结构面的方位有着密切的关系。顺层边坡是指岩层走向和倾向一致的边坡。实际工程中,常将走向与岩层走向夹角小于20°、层面倾向与边坡倾向接近的边坡视为顺层边坡[3]。顺坡结构面的存在及其特征对于边坡的变形和破坏方式及规模具有决定性的控制作用。无论从位移、拉应力区还是屈服区的分布特点来看,顺坡结构面在很大程度上削弱了岩体的稳定性。

2 存在的问题

目前对于顺层边坡的破坏机理,破坏模式,岩移规律的研究取得了很大的进展,针对不同的破坏模式,国内不少学者提出了各自的计算方法[4-8]。在这些计算方法指导下对顺层边坡的防治与加固也取得了可喜的成绩,然而对如何计算顺层边坡的安全系数的研究还不是很完善。边坡破坏模式的研究是从破坏形态规律性的认识开始的。顺层边坡的变形破坏模式有很多,按运动方式分有平面旋转滑动类、解体滑动类、层状结构渐进破坏类、溃屈破坏类等。顺层结构面的存在对边坡的变形破坏具有决定性的控制作用。从位移、拉应力区和屈服区的分布特点来看,顺层结构面在很大程度上削弱了岩体的稳定性。研究表明,对于顺层边坡,在进行稳定性评价时,选择圆弧型滑坡模式或者折线进行稳定验算是很难得到正确的结果。

近年来通过工程实践、数值计算分析、模拟试验方法,国内外对于顺层边坡破坏模式、岩移机理等的研究已经取得了一些成果,但这些经验都有很大的局限性。在工程领域,在边坡设计和稳定性评价时,一般依据各向同性介质理论,采用极限应力法确定近似圆弧滑面,作为边坡稳定性计算和设计参数选择的依据。但对于顺层边坡,破坏模式由顺层结构面控制,由于结构面的复杂性用简单的极限平衡法来分析稳定性显然是不适合的。在数值计算方面,通过有限元、离散元、流形元等方法对层状边坡的变形破坏机理进行了研究,如结构面的强度,层面倾向与边坡倾向的关系,层面倾角等因素对变形破坏的影响,数值分析得出了一些有用的结论。然而边坡稳定受多方面的影响,而各因素又有不确定性(模糊性、随机性、信息不完全性和未确定性)和复杂性,故无论是传统的确定性分析方法还是不确定性方法,其用于边坡稳定性分析与实际情况仍有很大的差距,在岩质边坡中最为明显。

3 某公路顺层岩质边坡地质概况

3.1 地形地貌

地貌单元属构造溶蚀低中山地貌类型,山顶高程一般945 m左右,路基标高816 m左右,与设计路线高差130 m左右,自然坡角32°,植被较发育。

3.2 地质构造

此段未发现大的构造现象,岩层产状基本稳定,产状为326°～ 336°＜38°～40°,发育三组节理裂隙,①58°＜76°为区域性节理,密度 0.7 m/条 ～2.0 m/条;② 节理 210°＜62°,密度 1.5 m/条 ～ 2.5 m/条,基本无充填,节理①切割节理②;③节理产状130°＜72°,间距 3 m ～ 5 m 。

3.3 地层岩性

基岩主要为三迭系嘉陵江组中厚层状灰岩,在K148+390～K148+440段,有泥灰岩出露,该岩层厚度约20 m,表层以强风化为主,局部有角砾灰岩和炭质灰岩,岩性较软弱,薄层、破碎稳定性较差,其它主要为弱风化中层层灰岩,陕薄层灰岩,局部薄层灰岩有一定破度(约1 m)使其岩层面有小的波浪状,灰岩中有方解石脉较发育,岩层坚硬,地表裂面粗糙,附黄色铁锰质薄膜及白色钙质薄膜。

3.4 水文地质条件

地表水无汇聚条件,地下水主要是地表降水漫流后下渗的雨水,主要赋存于岩溶裂隙中的裂隙水,水文地质条件比较简单。

3.5 工程特性

根据实测,此处边坡最大高度约60 m,坡比主要为1∶0.75,坡角大于岩层倾角,层滑动容易导致顺层滑动。

4 边坡岩体破坏模式及分析

4.1 灰岩节理与层面的组合破坏

节理②基本平行坡面,与坡面形成小角度斜交,一般地切割多个层位,节理①基本垂直于路线走向,为区域性节理,贯穿长度大,它将坡面中的岩体分割成块状。因此该段边坡潜在的失稳模式有沿节理②的组合形成拉伸面,节理①将边坡岩体两端分隔,坡面岩体沿岩层面滑动,岩层面的强度为边坡失稳的控制强度。嘉陵江组灰岩层面基本无软弱夹层,但层间较平直,且容易在层间张开,因此层间抗剪强度为坡面的弱面强度,对边坡岩体失稳起控制因素的作用。结合边坡岩特性和地形地貌特征,强降雨条件下,切方边坡上的高自然边坡,温流下渗的地下水可在裂隙中形成一定水头的静水压力,主要在坡体的中下部汇集,而坡体表面由于节理发育且张开无充填,地下水易沿裂隙面渗出,地下水对坡面的软化作用不大,但其静水压力为向坡外的推力,不利于边坡稳定,可在边坡的中下部有地下水渗出的漏头附近布设坡面深层排水孔,减少地下水对坡面稳定的负面作用。爆破振动对坡面中岩层间的粘结强度和完整性有较大的影响,大炮振动减少甚至消失岩层间固有粘结力,振动破坏使岩层大块体变成小块体,也减少了层间的强度。在稳定分析计算时需要考虑坡面岩层的长期强度和地下水,爆破对岩层强度的影响。

4.2 泥灰岩节理与层面的组合破坏

在此段边坡的K148+390～K148+440段坡面中,出露有岩性较软弱的泥灰岩,其岩体强度明显低于中厚层状灰岩易变形,在泥灰岩层中,还有岩层间泥质成分较高,使层间强度接近软岩,另外,软弱夹层遇水后强度降低明显,它不同于同坡面大桩号外的灰岩层面。因此,K148+390～K148+440段坡面潜在失稳的模式受薄层泥灰岩及软弱夹层的强度变形特性控制。

4.3 泥灰岩在坡面背后的分布及稳定性分析

根据灰岩、泥灰岩沉积特性,在坡面K148+500附近的岩下部即坡面内较浅处应有薄层破碎的稳定性较差的泥灰岩。在这里,切层坡面角大于岩层倾角,在坡面中泥灰岩厚度内,在坡脚处,如果有该层出露,则坡面的稳定性主要受泥灰岩强度和变形特性影响。若在坡脚处出露为岩性较好的中存层状灰岩,但厚度不大,坡内20 m深度内主要为泥灰岩,则要考虑坡面角,岩层倾角,灰岩和泥灰岩的厚度及分布具体对坡面进行稳定性计算分析,当中存层灰岩超过一定厚度时,泥灰岩隐含层对坡面稳定性影响较小时,则主要考虑灰岩的节理和层面组合破坏模式。

5 计算模型及计算方案

5.1 UDEC简介

刚体离散单元法一般认为Cundall于1971年提出来的[9]。该法适用于研究在准静力或动力条件下的节理系统或块体集合的力学问题,最初用来分析岩石边坡的运动。该法是在牛顿第二定律的基础上建立起来的,假设块体为准刚度体,块体运动主要受节理或弱面控制。刚性块体的假设对于应力水平较低的问题,如边坡稳定,是合理的。将节理岩体视为由裂隙切割的非连续介质,相互切割的裂隙将岩体分成相互独立的块体单元,单元之间可以看成是角-角接触、角-边接触或边-边接触。块体间的边-边接触可分解为由两个角-边接触而成,并且随着单元的平移和转动,允许调整各个单元之间的接触关系,最终块体单元可能达到平衡状态,也可能一直运动下去。这些块体在平衡条件发生变化时,块体之间就产生相互作用力,从而导致块体产生一定的加速度和位移,使块体的空间位置和状态发生变化。运动的块体之间,由于差异位移矢量的存在,从而使块体之间又发生新的作用力,根据新的力系,又可以计算出来各个块体在新的力系下的加速度、位移及新的运动位置。如此反复迭代直到整个体系在新的力系作用下达到平衡状态为止,这样整个岩体的破坏运动过程就被真实的模拟出来。

5.2 计算模型和计算参数

采用UDEC计算,离散元块体模型中主要考虑的结构面有节理②和岩体层面,将岩体层面和节理面的间距概化为5 m与4 m,层面完全贯通,节理面迹长有一定的间隙(即不完全贯通)。边坡几何尺寸见图1、UDEC模型见图2、差分网格见图3。表1为计算所采用的参数。

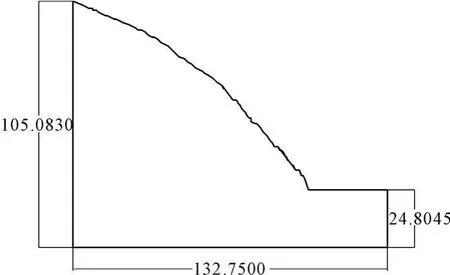
图1 边坡的几何尺寸(m)

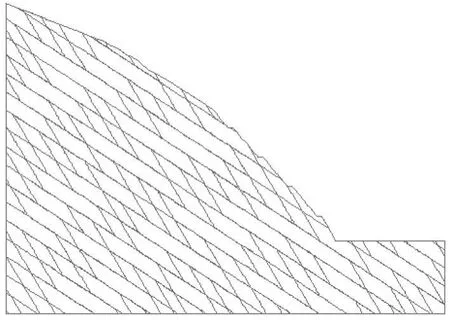
图2 UDEC计算模型

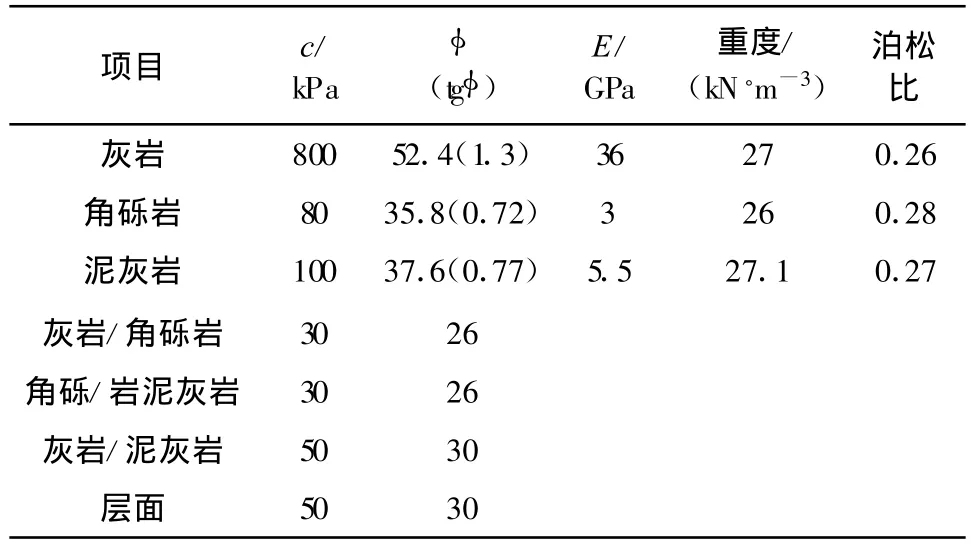
表1 计算参数

5.3 计算方案

计算分为3种情况,第1种情况考虑边坡开挖完成后,角砾岩(泥灰岩层)在坡角处出露;第2种情况考虑边坡开挖完成后,软岩体(角砾岩和泥灰岩层)在坡角处下部5 m深度处出现;第3种情况考虑边坡开挖完成后,软岩体在坡角处下部埋深15 m。对应3个计算模型(计算剖面),详见图4。

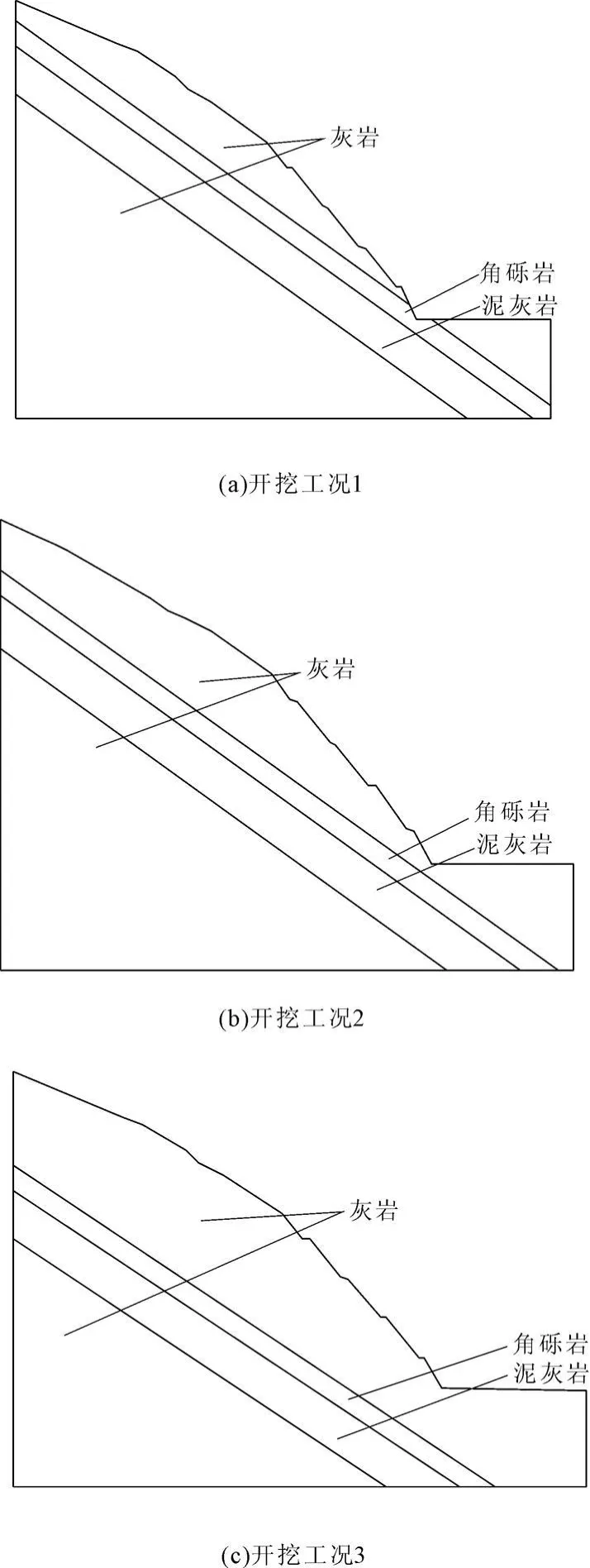
图4 各计算方案几何物理模型

6 计算结果分析

(1)模型一,角砾岩在坡角处出露,岩体的软弱层面对边坡的破坏模式起控制作用。在坡体后部,岩体沿节理面滑动,进入软弱岩层后,岩体失稳时将沿岩层的软弱层面发生滑动,在坡角剪出。塑性变形区集中在角砾岩与泥灰岩层内部,灰岩层内无塑性区。边坡在该模式下的安全系数为fos=0.82。模型的材料分区、极限状态时由速度矢量确定的潜在滑动面位置、滑动面滑体厚度和塑性区分别见图5、图 6。

图5 模型1在极限状态时由速度矢量

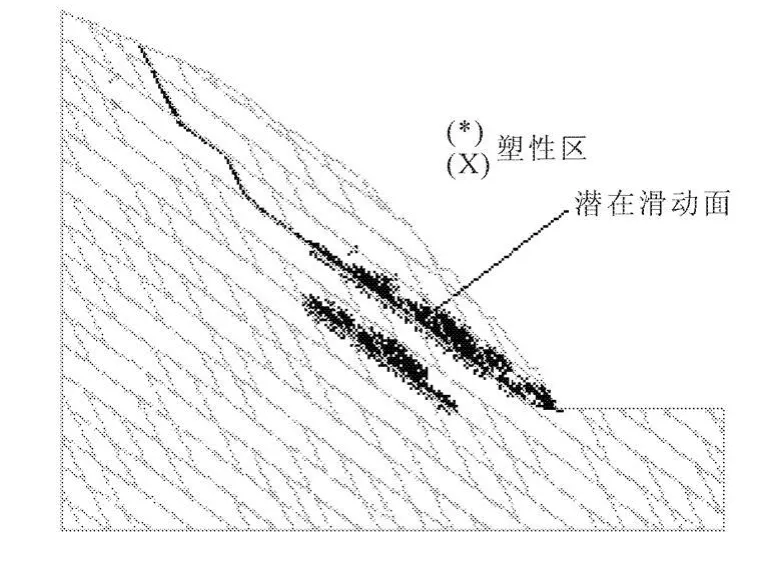
图6 模型1的塑性区

(2)模型二,软岩体(角砾岩和泥灰岩层)在坡角处下部5 m深度处出现,角砾岩和泥灰岩控制边坡的破坏。岩体的滑动面主要在软岩体内,沿软弱层面滑动时,在坡角将切割层状灰岩体向外剪出,坡角处的灰岩层有可能发生挤压破坏。塑性变形区主要集中在角砾岩与泥灰岩层内部,灰岩层内无塑性区。滑体厚度达到25 m。边坡在该模式下的安全系数为fos=0.91。模型的材料分区、极限状态时由速度矢量确定的潜在滑动面位置、滑动面滑体厚度和塑性区分别见图7、图8。

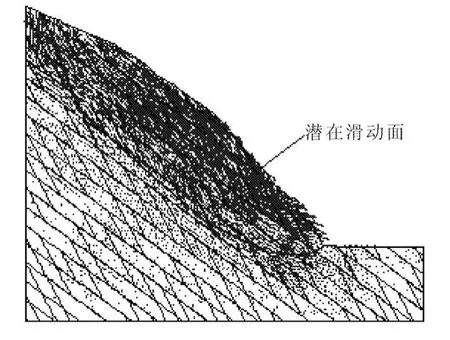
图7 模型2在极限状态时由速度矢量

(3)模型三,软岩体(角砾岩和泥灰岩层)在坡角处下部15 m深度处出现,塑性变形区虽然集中在角砾岩与泥灰岩层内部,但角砾岩和泥灰岩对边坡的破坏影响不大,边坡处于极限平衡状态时,岩体滑动主要发生在灰岩中,灰岩层内无塑性区。边坡在该模式下的安全系数为fos=1.06。模型的材料分区、极限状态时由速度矢量确定的潜在滑动面位置、滑动面滑体厚度和塑性区分别见图9、图10。

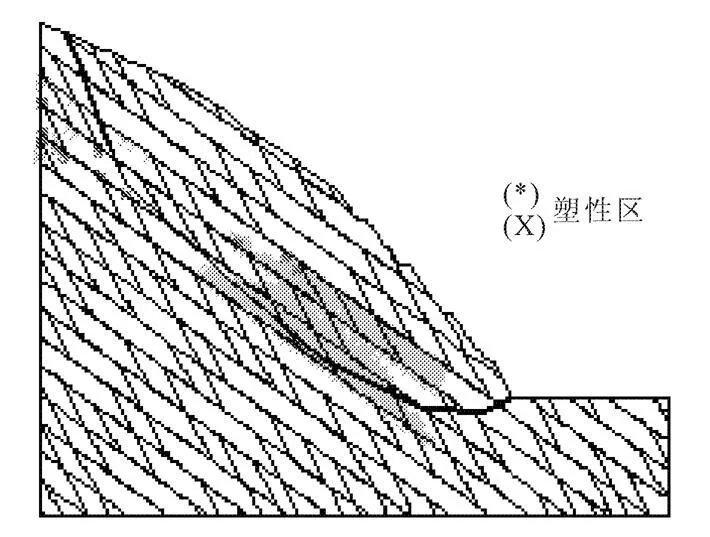
图8 模型2的塑性区

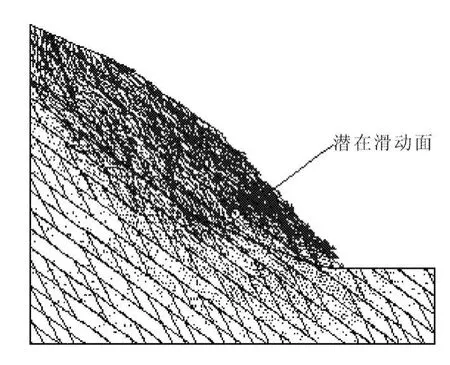
图9 模型3在极限状态时由速度矢量

7 结论与建议

经过上述分析可知,在该路段开挖时,最好不要切坡太深,尽量避免较为软弱的角砾岩或泥灰岩出露,否则边坡安全性将极大的降低。可通过适当抬高路基开挖高程和外帮措施尽量减小切坡深度,从而保证边坡稳定。最优开挖方案是保证角砾岩或泥灰岩埋藏深度不小于15 m。

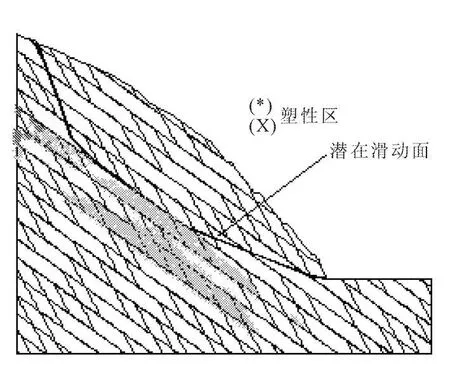
图10 模型3的塑性区

[1]崔政权,李宁.边坡工程—理论与实践最新发展[M].北京:中国水利水电出版社,1999.

[2]郭 志.实用岩体力学[M].北京:地震出版社,1996.

[3]邓荣贵,周德培,李安洪,等.顺层岩质边坡不稳定岩层临界长度分析[J].岩土工程学报,2002,24(2):177-182.

[4]刘均.顺层边坡溃层问题的计算方法[J].水文地质工程地质,1997,(6):37-40.

[5]李树森,任光明,左三胜.层状结构岩体顺层斜坡失稳机理的力学分析[J].地质灾害与环境保护,1995,(2):24-29.

[6]李荣强.突变理论在顺层边坡稳定分析中的应用[J].同济大学学报,1993,(3):379-386.

[7]杨天鸿,芮勇勤,李连崇,等.顺层蠕动边坡变形破坏机理及其稳定性动态分析[J].工程地质学报,2003,11(2):155-161.

[8]金仁祥,杨良策,任光明,等.三峡库区某公路顺层岩质边坡变形特征分析[J].地质灾害与环境保护,2003,14(2):39-42.

[9]Cundall P A.A computer model for simulating progressive large scale movements in blocky systems[C]//Proceedings of the Symposium of the International Society of Rock Mechanics,1971,1(Ⅱ):1-8.