多通道FULMS自适应前馈振动控制算法分析与验证

朱晓锦，黄全振，高志远，高守玮，姜恩宇

(上海大学 机电工程与自动化学院，上海 200072)

大型空间柔性结构如太阳能帆板，在轨运行期间必须保证很高的运行精度，对结构振动水平和控制要求极其严格，如何有效降低或消除结构振动响应已成为当今研究的热点。许多学者已做了大量的研究，并提出了一些有效的控制算法，但很多算法仅获得了初步实现，发展并不成熟。文献［1］采用模态控制算法，并在弹性结构主动控制中得到了较好的效果，但由于自适应结构是分布参数系统，往往会产生观测溢出和控制溢出;文献［2］以牺牲模态截断阶数来避免控制和观测溢出;文献［3］提出了一种模糊预测控制方法，有效地避免控制和观测溢出，但仅处于仿真阶段。文献［4－7］在FXLMS算法基础上发展了Delayed-LMS算法、FSLMS算法以及多误差LMS算法等，但实际试验过程也均存在尚未能解决的相关问题。

由于FXLMS(filtered-X least mean square)控制算法具有控制修正速率高、对非平稳响应适应能力强，并能够较快跟踪结构参数及外扰响应变化的特性，近年来在振动主动控制领域获得广泛关注［8－9］;但其具有需要预知与外激扰信号相关参考信号的不足，目前实验室中常直接取自振源信号，导致实际应用具有一定的不现实性。FULMS(filtered-U least mean square)算法可以从振动结构响应中提取参考信号，同时能够抑制振动反馈可能带来控制系统不稳定，并具有较低阶滤波器结构的优点。本文以压电机敏帆板结构为模拟试验对象，采用FULMS控制算法直接从受控结构响应中提取参考信号，针对算法结构和算法过程进行研究，并利用MATLAB平台进行算法过程的仿真分析，同时构建实验结构和测控平台进行实验验证;仿真分析与实验结果表明，FULMS算法相对于FXLMS算法，具有较快的收敛性和较好的控制效果，研究结果为航天柔性结构振动主动控制提供了相关方法思路。

1 FULMS算法振动控制结构

自适应滤波结构振动主动控制方法是以抵消外扰引起的受控对象的响应为出发点，基本思想如图1所示;控制器根据误差传感器的振动信号，输出控制信号给作动器，使其产生控制力作用于受控对象，使受控对象的振动响应与外扰响应相抵消，达到消除或减小受控对象振动响应的目的。

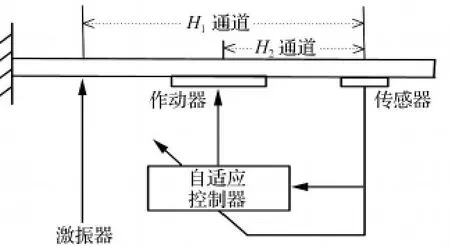
图1 振动控制系统示意图Fig.1 Schematic diagram of vibration control system

图1中H1通道表示从激振器到误差传感器的传递函数，H2通道表示从次级振源到误差传感器的传递函数。从控制器设计和自适应算法分析简单性考虑，多通道FULMS算法控制器结构可构建如图2所示。

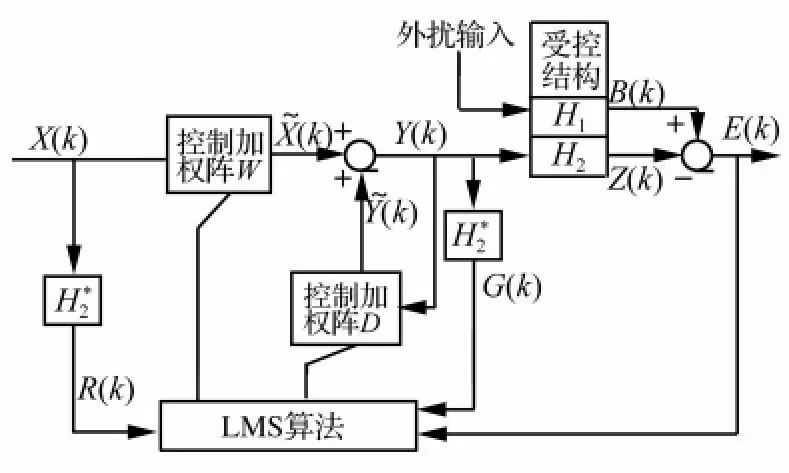
图2 FULMS振动控制算法结构图Fig.2 Block diagram of FULMS vibration control algorithm

图2所示，X(k)为滤波器输入向量，Y(k)为M维控制器k时刻的输出向量，E(k)为L时刻受控对象响应误差输出向量，H1、H2分别为描述外扰通道和控制通道特性的结构模型参数向量;由于控制通道H2引入导致系统产生了延迟，外扰通道如果没有相同长度延迟就不能得到补偿，将导致系统不稳定。为此，在参考信号与更新权系数LMS算法之间，加入一个对H2辨识滤波器对X(k)进行滤波。

2 FULMS控制算法过程与分析

滤波－U最小均方算法(FULMS)的完整形式由L.J.Eriksson 提出［10］。多通道 FULMS 控制算法的结构原理如图2所示，该控制系统具有M个控制器和L个传感器，控制算法相当于有两个滤波器组成，分别为前馈滤波器和反馈滤波器，其滤波器的长度分别设为P和Q。外扰输入信号经过传输通道H1之后，产生作用于结构对象的L维外激扰响应输出向量B(k)，控制器的控制输出Y(k)由权值矩阵W*(k)和输入向量U(k)得出。

为解释方便，首先列出单通道控制输出如下:

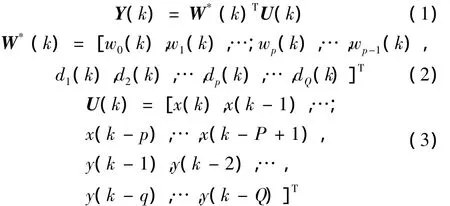
上述式中:x(k－p)为x(k)的p阶延迟输入，y(kp)为y(k)的q阶延迟输出，其中p和q为延迟量，取之范围为 p=0，1，…，P －1，q=1，2，…，Q。x(k)为滤波器在k时刻的参考信号，其要求与原始外扰输入信号有较高的相关性。

FULMS算法推导过程简列如下［11］:

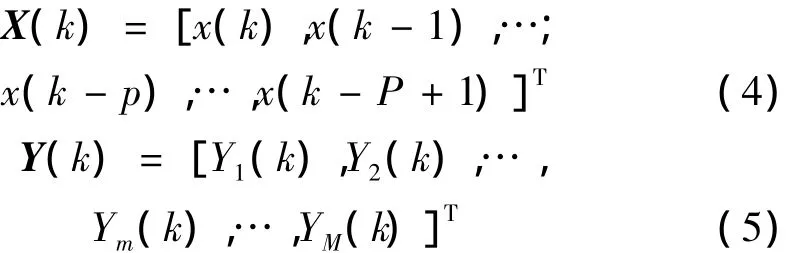
其中:

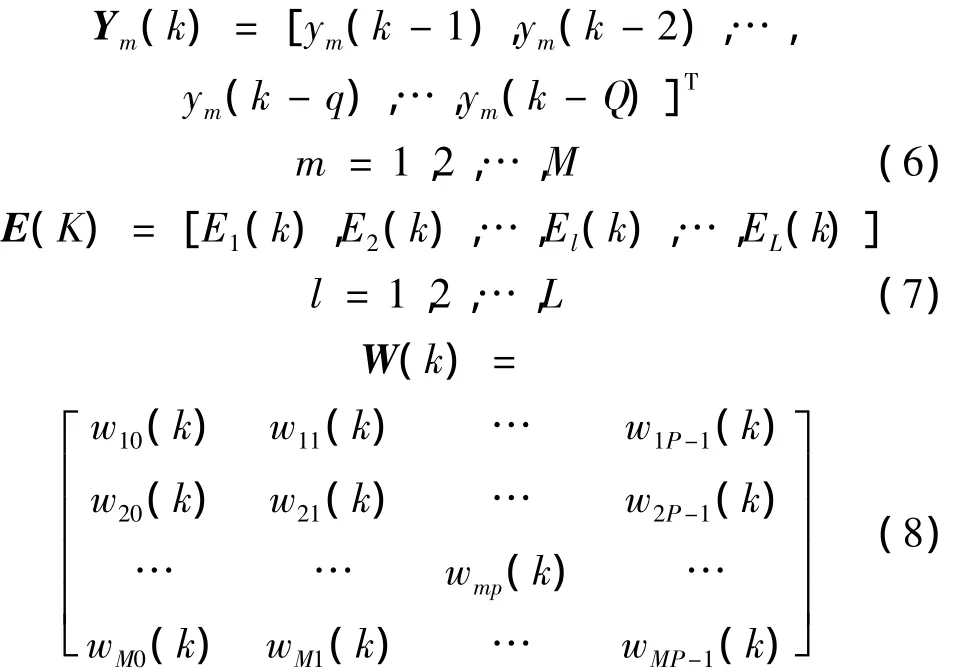
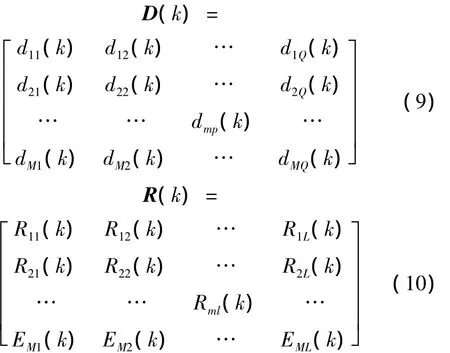
其中:

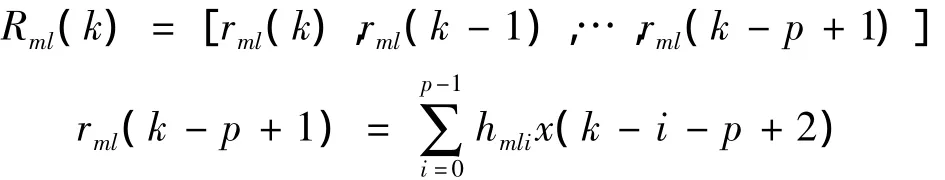
式中:m=1，2，…，M，l=1，2，…，l。

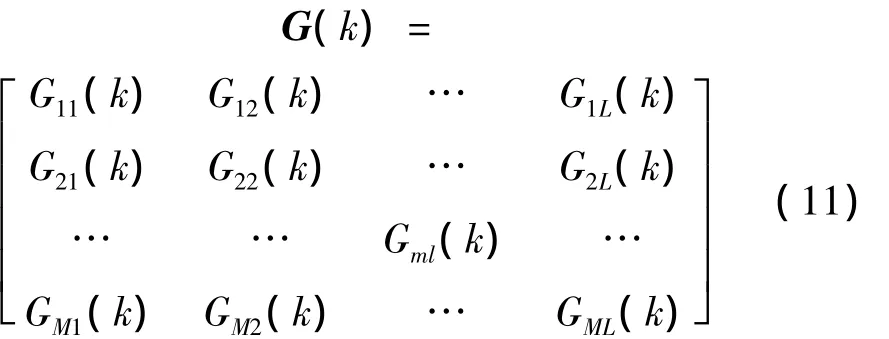
其中:

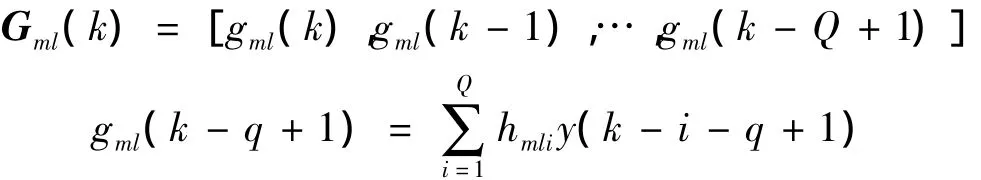
式中:m=1，2，…，M，l=1，2，…，L。

式(8)中W(k)是M×P阶控制器加权系数矩阵，P为滤波器参考信号的阶数，wmp(k)为第k时刻的前馈滤波器第m个控制器加权系数向量的第p阶元素;D(k)是M×Q阶的加权系数矩阵，dmq(k)为第k时刻的反馈滤波器第m个控制器输出信号加权系数向量的第q阶元素。R(k)为滤波－X信号矩阵，由X(k)经环节得到;G(k)也是滤波－X信号矩阵，由Y(k)经环节得到。

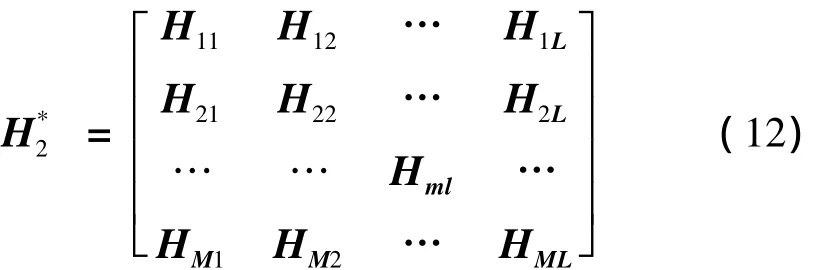
式(12)中，Hml=［hml1，hml2，…，hmlf，…，hmlF，］，其中:f=1，2，…，F，F为模型辨识过程中，根据辨识精度要求，而人为定义的辨识模型描述阶数。

根据上述式(1)至(12)，可得受控对象响应误差输出为:

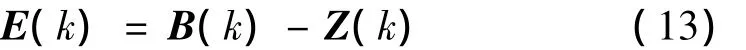
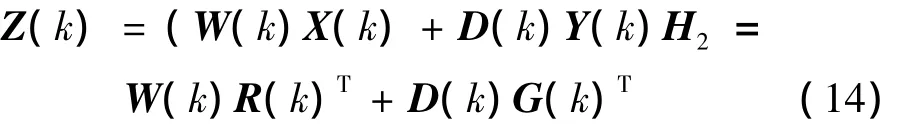
控制过程实质上就是寻求最优的W和D过程，并依据最小均方准则使L个误差信号的均方值达到极小。根据LMS算法准则，取性能目标函数为:

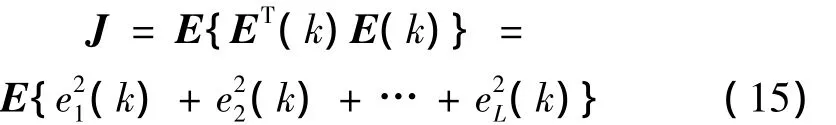
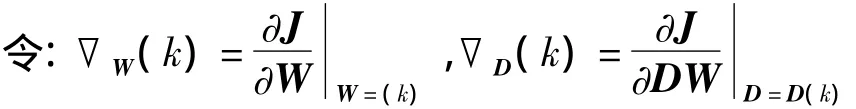
则有:

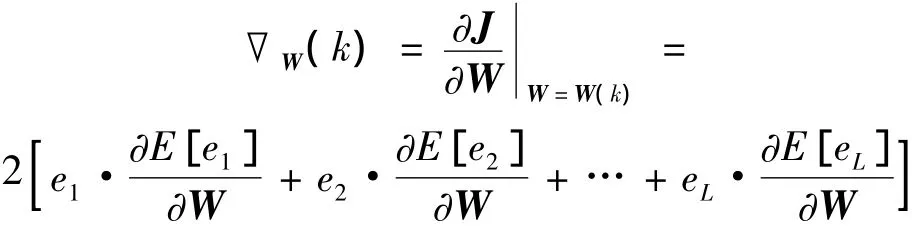
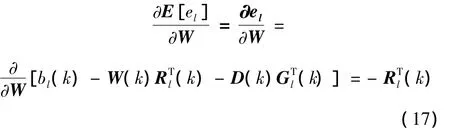
由式(16)和式(17)可得:

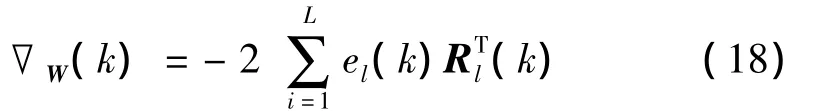
根据最小均方算法的定义，有:

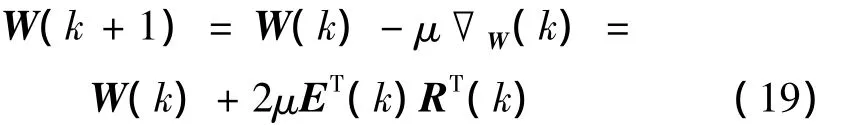
式(19)中，μ为步长收敛因子，其值由X的自相关矩阵的特征值来确定。

同理:

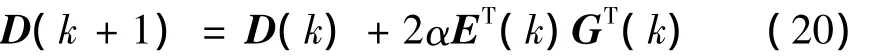
式(20)中，α为步长收敛因子，其值由Y的自相关矩阵的特征值来确定。

根据以上推导过程，多通道 FULMS算法可表示为:

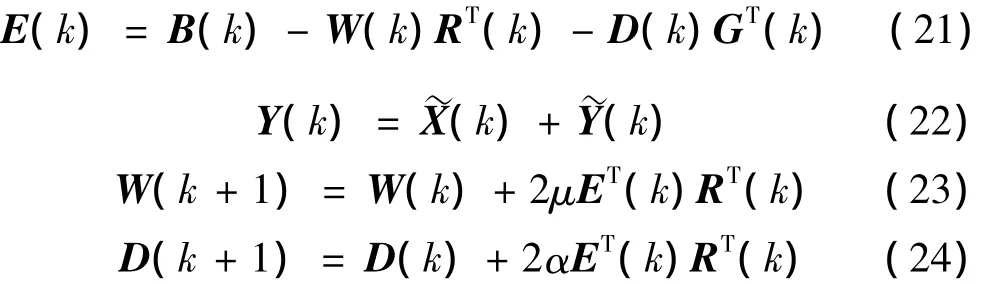
这里，式(22)中具有下列关系:

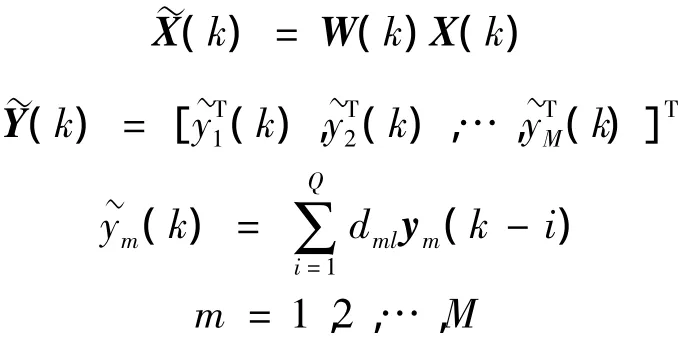
3 实验分析与验证

具体实验模型模拟航天太阳能帆板结构，采用悬臂板方式建立，柔性基板采用环氧树脂板，并分布粘贴PZT传感和驱动网络构建机敏压电柔性结构。基板主要参数为:弹性模量Ep=65 GPa，泊松比 ν=0.3，密度ρ=7500kg/m3;尺寸为1500mm ×400mm ×1.5mm。同时，根据模型结构特性、压电陶瓷材料(PZT)元件特性和环境阻尼等，采用Bayard提出的D优化设计准则［12］，配置一个4×4传感/驱动PZT网络的实验模型结构，布置方案如图3所示。

图3 传感/驱动布置网络图Fig.3 Schematic diagram of sensor/actuator placement

图3中，压电传感PZT重量为每片1.67 g，尺寸规格为40mm×8mm×1mm，且每片压电传感器为一个测量通道，图中4个传感器编号分别为1－4，即传感器有4个通道;压电驱动器重量为每片30 g，尺寸规格为65mm×30mm×2mm，每一竖排的压电片作为一组执行机构，根部的三组组合成一个通道，另外三组分别是三个通道，分别编号1－4，即驱动器也有4个通道。此外为增强驱动能力，在结构双面进行压电驱动器的对位粘贴。

首先利用ANSYS 9.0有限元分析软件，进行实验模型结构的模态分析，并获得结构模型50Hz之内的主要模态频率;同时，针对实验模型结构进行实际的扫频实验，实测出模型结构50Hz之内的主要模态频率，并与有限元分析结果进行对比，获知最大误差在5%之内，表明理论分析与实测结果比较接近。在进行算法仿真分析与实际控制实验过程中，截取模型前五阶实测模态频率为实验参数，其值分别为:FREQ1=0.62Hz，FREQ2=3.91Hz，FREQ3=10.95Hz，FREQ4=21.47Hz，FREQ5=35.5Hz。

其次基于Matlab7.1软件平台，进行单通道方式和多通道方式的两种控制算法仿真分析;在此基础上，基于分布式压电PZT传感/驱动网络，以及实验模型结构和相关测控系统，进行基于多通道FULMS算法的结构振动控制实验分析与验证。此外，在相同实验条件下，同时基于多通道FXLMS算法进行结构振动控制实验验证。由此，实现两种控制算法分别在单通道和多通道模式下，以及仿真分析与实验验证方式下的相关控制效果对比与分析。

3.1 控制算法单通道模式仿真分析

基于Matlab7.1软件平台，进行控制算法单通道模式仿真分析，具体参数设定为:激振频率f=10.95Hz，采样频率fc=300Hz，步长收敛因子μ=0.01，自适应滤波器长度定义为12(FULMS算法为p+q=12，FXLMS算法为p=12)，迭代次数为1500次;基于上述参数设置，针对FULMS和FXLMS两种控制算法进行了仿真分析，取较为直观的控制效果误差输出图和系统收敛权系数曲线图进行对比，仿真结果如下图4(a)、4(b)、5(a)、5(b)所示。

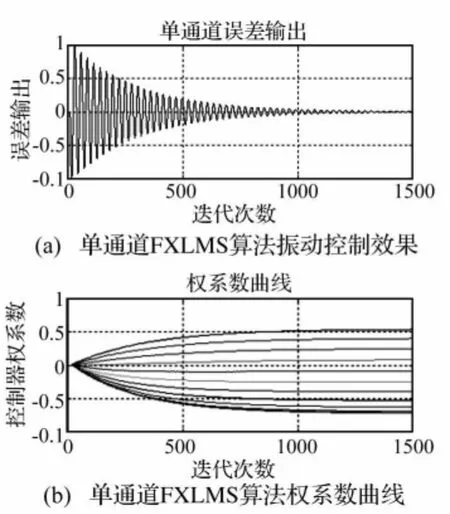
图4 Fig.4 (a)Vibration effect of single-channel FXLMS algorithm(b)Weight coefficient curves of single－channel FXLMS

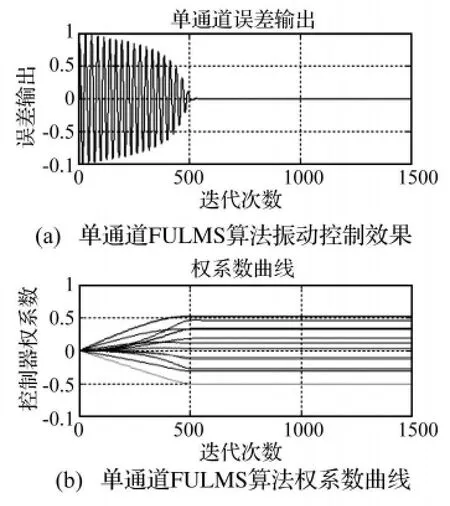
图5 Fig.5 (a)Vibration effect of single-channel FULMS algorithm(b)Weight coefficient curves of single－channel FULMS

由上述图中所见，系统在施加FXLMS控制算法后，结构振动响应经过1000步迭代才获得了大幅度的抑制，而在施加FULMS算法后，结构振动响应只经过500步迭代就获得了大幅度的抑制，从权系数变化曲线可知，FULMS算法较之于FXLMS算法，收敛速度明显加快。

3.2 控制算法多通道模式仿真分析

为更好地反映控制效果，采用多输入多输出控制方式(4通道)，进行FXLMS与FULMS控制算法仿真分析;具体设置参数如下:激振频率f=10.95Hz，采样频率fc=300Hz，步长收敛因子μ=0.01，自适应滤波器长度12(FULMS算法为p+q=12，FXLMS算法为p=12)，迭代次数为800次;具体分析结果，取通道1和通道3的振动控制效果图，即通道1和通道3误差输出图进行效果对比。仿真结果如下图6(a)、图6(b)、图6(c)、图7(a)、图7(b)、图7(c)所示。

图6 Fig.6 (a)Performance of multichannel FXLMS at channel 1(b)Performance of multichannel FXLMS at channel 3(c)Weight coefficient curves of multichannel FXLMS

图7 Fig.7 (a)Performance of multichannel FULMS at channel 1(b)Performance of multichannel FULMS at channel 3(c)Weight coefficient curves of multichannel FULMS

由上述图示可知，在施加FULMS控制算法后，在迭代250步左右后，结构振动响应获得明显抑制，而FXLMS算法达到同样效果，则需要450步左右，表明FULMS算法具有较快的抑振速度和良好的控制效果，此外较之于单通道控制仿真分析，多通道控制综合抑振效果显现更为有效。但是，由于FULMS算法中采用了反馈回路，使控制系统引入了极点，为追求抑制速度而相应提高步长因子时，则较易引起系统发散，虽然仅从图6(c)和图7(c)中观察，系统没有出现发散现象，且FULMS算法收敛速度更快，但系统控制发散的隐患是存在的。

3.3 多通道模式控制算法实验验证

压电机敏柔性结构振动主动控制实验平台的构建，硬件系统主要由固定支撑架构、实验模型对象、高性能计算机、高速数据AD采集卡与DA输出卡、信号发生器、低通滤波器、示波器、激振器、功率放大器，以及相关测控单元等组成。

实验台架结构包括支撑钢板结构，具体尺寸为长宽高600mm×600mm×25mm，并在铺垫橡胶垫的基础上安装于支撑试验台面上，以尽量减小模型对象振动响应向基础试验台面的传递，同时实验台架安装有悬臂固支杆、激振器定位结构，以及导线接线排等;激振器作为外扰激励源对结构模型对象进行激励，具体型号为江苏联能JZK－10;高速数据AD采集卡为研华公司的PIC－1712，DA输出卡为研华公司PIC－1721，两卡均为12位精度，PCI连接方式，并与高性能计算机构成核心控制器硬件部分，整体实验平台构成如图8所示。

图8 整体试验平台结构图Fig.8 Structure chart of experimental setup

在构建实验平台的基础上，基于VC6.0平台开发了相关测控软件，以保障系统功能实现与控制过程实施。基本控制过程为:基于激振器对实验模型进行持续激励，压电传感网络产生的结构振动信号，经信号调理后由AD卡实现多路采集，并由计算机运算控制算法，同时产生多路输出控制量由DA卡输出，并经功率放大器驱动压电作动网络，以实现模型结构振动响应的多通道自适应控制。

具体实验过程中，激振器持续对模型结构进行激励，同时在结构持续受激状况下启动控制过程，已验证模型结构的振动自适应对消效果。在此优选5阶模态激振信号f=35.5Hz的情况，予以控制效果的分析对比;取滤波器的长度为24阶，收敛因子为μ=0.01，参考信号取自AD3(即3通道)。首先进行多通道FXLMS算法控制实验，观察控制效果和记录实验数据，并在相同的条件下，进行多通道FULMS算法控制实验;在此基础上，针对实际获得的实验数据进行分析，具体如图9、图10和图11所示。

其中，图9(a)、图9(b)分别为采用FXLMS算法控制时，控制通道1和控制通道2的振幅变化图;图10(a)、图10(b)分别为采用FULMS算法控制时，控制通道1和控制通道2的振幅变化图;图11(a)、图11(b)分别为通道1施加FULMS控制前后的功率谱。由上述图中可见，FULMS算法的控制效果明显优于FXLMS算法;由图9可见，在施加FXLMS控制后，振动响应得到大幅度的抑制时间需要4.5秒左右;由图10可见，在施加FULMS控制后，振动响应得到大幅度抑制的时间仅为3秒左右，同时没有出现控制发散现象。

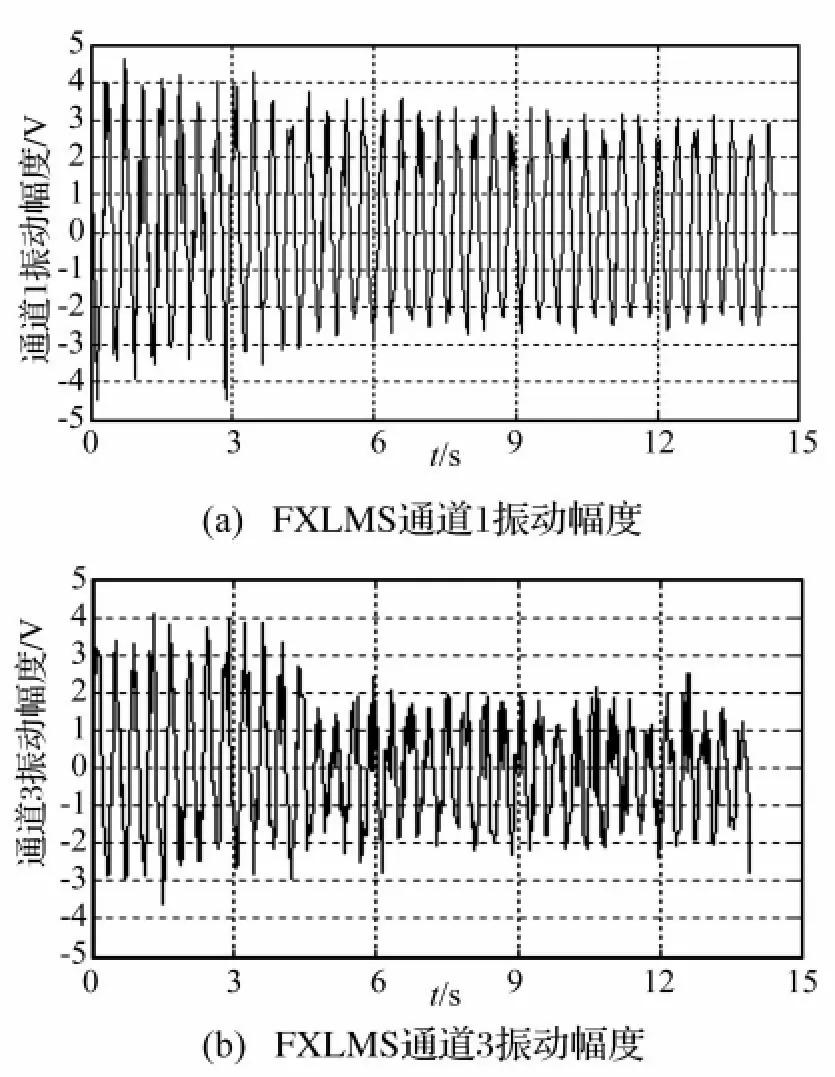
图9 Fig.9 (a)The amplitude of the vibration at channel 1 on FXLMS(b)The amplitude of the vibration at channel 3 on FXLMS

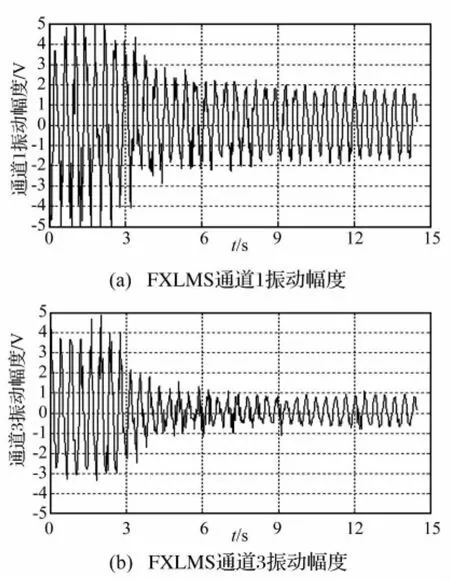
图10 Fig.10 (a)The amplitude of the vibration at channel 1 on FULMS(b)The amplitude of the vibration at channel 3 on FULMS

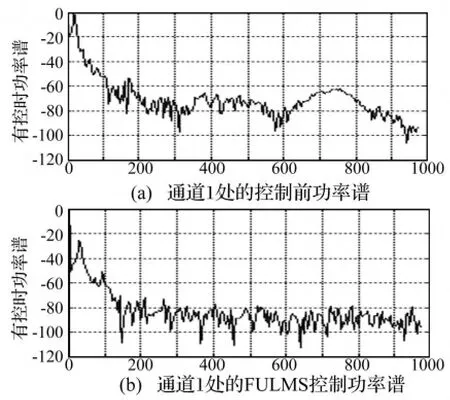
图11 Fig.11 (a)Power spectrum at channel 1 without controlFig.11 (b)Power spectrum at channel 1 with control

虽然激振器采用单频激振模型结构，但结构动力响应不仅存在激振信号的频率成分，还包含了众多的谐波成分，这中间即有结构其它模态的耦合响应，同时也由于激振器的安装原因以及激振信号的不纯所造成。由图11可见，通道1功率谱幅度控制前后抵消比约为25dB，另外从噪声控制的角度来说，在抑制结构振动响应的同时，由结构振动所引起的噪声辐射也得到了一定程度的降低。

4 结论

针对 FXLMS结构振动控制算法的不足，基于FULMS控制算法进行了压电柔性结构自适应振动控制分析与验证;控制思路上直接从振动结构响应中提取参考信号，分析设计FULMS自适应前馈振动控制结构和系统，并在此基础上构建实验模型结构和测控系统，基于多通道FULMS控制算法进行控制分析与实验验证。同时为了验证FULMS算法的可行性和优越性，较之FXLMS控制算法进行了对比分析与实验;实验分析与验证结果表明，FULMS控制算法比FXLMS控制算法收敛速度更快，且控制效果更为有效，相关技术方法的探索和验证，为进一步深入研究奠定了基础。

［1］Scott E，Vlattas J.Modal analysis and active vibration control of the naval postgraduate school space truss［D］.Monterey，CA，USA:Naval Postgraduate School，1998，91 －94.

［2］WU Hongxin， LIU Yiwu， LIU Zhonghan， et al.Characteristic modelling and the control of flexible structure［J］.Science in China(Se.F)，2001，44(4):278 －291.

［3］师五喜，霍 伟，吴宏鑫.基于特征模型的柔性结构直接自适应模糊预测控制［J］.控制理论与应用，2005，22(5):677－681.

［4］Glugla M，Schulz R K.Active vibration control using delay compensated LMS algorithm by modified gradients［J］.Journal of Low Frequency Noise Vibration and Active Control，2008，27(1):65－74.

［5］胡庆雷，马广富.基于滑模输出反馈与输入成形控制相结合的挠性航天器主动振动抑制方法［J］.振动与冲击，2007，26(6):133－138.

［6］Reddy E P，Das D P，Prabhu K M M.Fast exact multichannel FSLMS algorithm for active noise control［J］.Signal Processing，2009，89(5):952 －956.

［7］DeBrunner V E，Zhou Da yong.Hybrid filtered error LMS algorithm another alternative to filtered-x LMS［J］.IEEE Transactions on circuits and systems， 2006， 53(3):653－661.

［8］Vaudrey M A，Baumann W T，Saunders W R.Stability and operating constraints of adaptive LMS-based feedback control［J］.Automatica，2003，39(4):595 －605.

［9］Akhtar M T，Abe M，Kawamata M.A new variable step size LMS algorithm based method for improved online secondary path modeling in active noise control systems［J］.IEEE Transactions on Audio，Speech，and Language Processing，2006，14(2):720－726.

［10］Eriksson L J.Development of the filtered-U algorithm for active noise control［J］.Acoust.Soc.Am.1991，89(1):257－265.

［11］Montazeri A，Poshtan J.A Novel Technique for Design and Stability Analysis of Adaptive IIR Filters in ANVC Aplications［C］.ICSPC 2007:524－527.

［12］Bayard D S， Hadaegh F Y， Meldrum D R. Optimal experiment design for identification of large space structures［J］.Automatica，1988，24(3):357－364.