空气弹簧在机械振动台中的应用

赵晓敏

(西安三润环境设备科技有限责任公司，西安 710068)

空气弹簧是在一密闭容器中存储压力空气，利用空气的可压缩性实现弹簧作用。空气弹簧通常由弹簧本体、附加气室和高度控制阀三部分组成。根据结构，可分为囊式和膜式两种。囊式空气弹簧可根据需要设计成单曲、双曲和三曲；膜式空气弹簧则有约束膜式和自由膜式两种。机械振动台上使用的是约束膜式空气弹簧，约束膜式空气弹簧的优点是刚度小，并且特性曲线容易通过约束裙的形状来控制，缺点是由于橡胶簧的工作状况复杂而使耐久性差。

在机械振动台单自由系统中，空气弹簧的作用主要为系统的支撑，作为系统的刚度和固有频率计算的重要环节和依据。所以，空气弹簧在机械振动系统中的应用以支撑刚度为主，减振隔振为副。

空气弹簧作隔振用时有以下优点：

（1）空气弹簧的刚度随载荷而变，因而在任何负载下自振频率几乎保持不变，使弹簧装置具有几乎不变的性能；

（2）空气弹簧具备非线性特性，能有效控制振动位移幅值；

（3）通过高度控制阀，可使空气弹簧的工作高度在任何载荷下保持一致，也可使弹簧在同一载荷下具有不同的高度，因此，有利于适应囊式和膜式多种结构上的要求；

（4）空气弹簧的刚度可以根据需要，借助于改变气室的容积进行选择，而且可以选择的很低；

（5）同一空气弹簧，能同时承受轴向和径向载荷，也能传递扭矩，而通过内压力的调整，还可以得到不同的承载能力，因此能适应多种载荷的需要；

（6）空气弹簧各个方向吸振效果好，吸收高频振动和隔音的性能好；

（7）在空气弹簧本体和附加空气室之间设一节流孔，能起到阻尼作用，如果节流阀孔径选择适当，可不设减振器。

1 空气弹簧受力分析

空气弹簧在机械振动台上使用时，其“约束膜式”受力模型如图1。

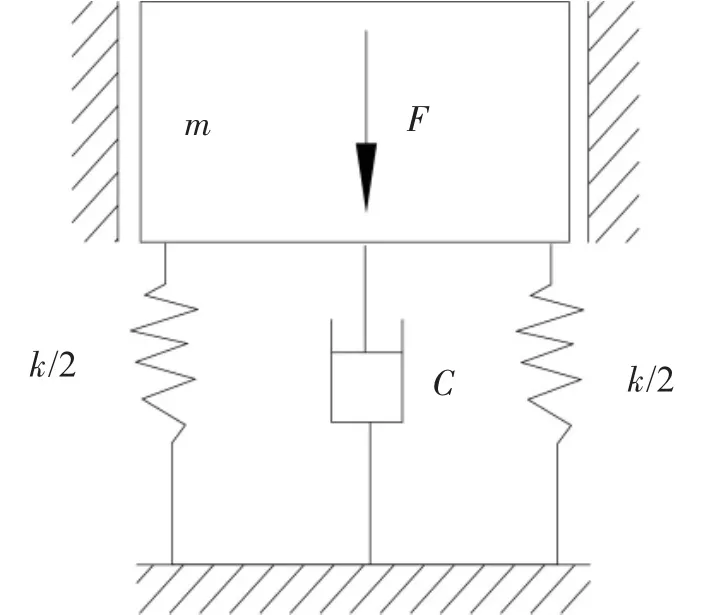
图1 空气弹簧在机械振动台上使用时受力模型

此受力模型为单自由度受迫振动系统，当振动体受垂直方向激振力Fsinωt的作用时，位移为usin ωt，其运动方程为：

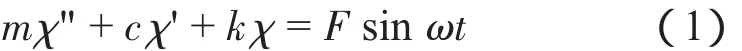
受迫振动的特解可表示为：

（1）、（2） 式中：m为质量，c为阻尼系数，k为刚度，X为振幅，χ为X的解，t为时间，Fsinωt为激振力，ω为激振频率，φ为相位差。

其中，振幅：

相位差为：

在以上的振幅和相位差计算公式中：

Xst=F/h——在与激振力幅值相等的静力P作用下系统的静位移

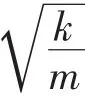
Cc=——临界阻尼系数。

可得：

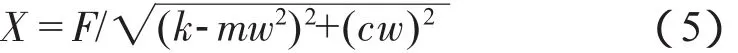
所以，传至地面的力不是Fsinwt，而是弹簧力kx和阻尼力cx'的和：

其幅值为：

将式(5）带入式(6），得:

因为 ξ=c/2ωnm，γ =ω/ωn，所以

倘若阻尼忽略不计，则（式2-7）变化为：

FT/F实际传递力的幅值与不平衡力的力值之比，称为传递率。分析式(8）可知，要使振动台的不平衡力不传递到底座，或者，要使底座的力不传到振动台，传递率FT/F要尽可能的小，即ω/ωn要尽可能大，也就是说ωn越小越好，即空气弹簧的一阶谐振频率尽可能低。

2 空气弹簧的设计

根据GB 2423.10《电工电子产品基本环境试验规程试验Fc：振动(正弦)试验方法》，机械振动台的工作下限频率f1小于或等于5 Hz。一般取空气弹簧一阶谐振频率f0≤（1/3-1/2）f1，空气弹簧受力简图如图2。

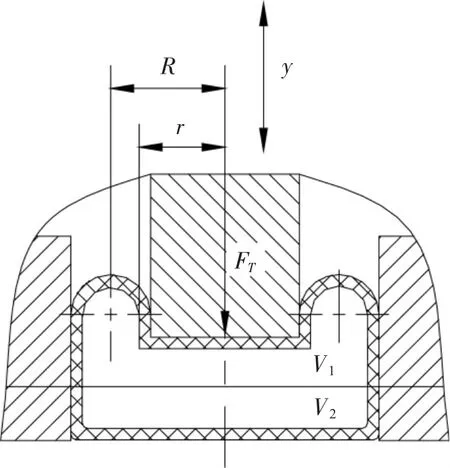
图2 空气弹簧受力时分析图

假定，空气弹簧变形前后，其橡胶囊经线（纵剖面）方向上断面保持不变；断面长度保持不变。

其中：

FT为空气弹簧承受的力；

Y为振动台振动时不平衡力作用引起空气弹簧振动，其位移幅值为y；

V1为空气弹簧标准状态下内容积；

V2为附加气室标准状态下内容积。

在标准状态下，根据静力学平衡原理，有：

其中，Pa为大气压力，一般取1 kgf/cm2

当空气弹簧以位移幅值y振动时，空气弹簧内容积的变化量为：

当空气弹簧向上振动时，内容积增大，压力减小，其内容积变为：

其压力变为：Pmin=P(V0/Vmax)m

其中，m为多变指数，1≤m≤1.4，在等温过程中，m=1；在绝热过程中，m=1.4。

当空气弹簧向下振动时，内容积减小，压力增大，其内容积变为：

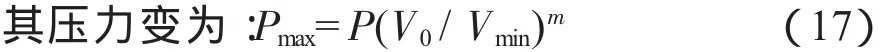
为使空气弹簧具备理想的非线性，可调整附加气室内容积V2，那么空气弹簧的轴向刚度为：

其中，dA/dy为有效承载面积变化率，根据前面受力分析时假定的条件，dA/dy=0，则空气弹簧的轴向刚度为：

同理，空气弹簧的径向刚度为：

其中，b为空气弹簧形状系数，b=π/(4r)；

k'为簧囊本身径向刚度；

A为空气弹簧的有效承载面积。

式中，g为重力加速度，一般取981 cm/s2。

在机械振动台上，4个空气弹簧分别连接4个气室，这4个气室又串联在一起，一阶谐振频率约5×(1/3)=1.78 Hz，所以机械台的一阶谐振频率较低。

所以，空气弹簧必须满足条件：

3 几个影响因素分析

气室与附加气室容积的比例，空气弹簧形状、材料、尺寸，以及气室与附加气室之间的节流孔的大小，对系统刚度和固有频率都有一定的影响。

（1）附加气室容积对系统刚度和一阶谐振频率的影响。由式（19）可看出，有效容积越大，轴向刚度越低。所以给空气弹簧连一附加空气室，可减少空气弹簧的轴向刚度。

以空气弹簧为弹性元件的空气悬架系统表现出了诸多的优越性，如果在此基础上再增加一附加气室组成带附加气室空气弹簧系统，还可以进一步提高悬架系统的减振性能。橡胶空气弹簧与附加空气室相连，可使橡胶空气弹簧装置的固有振动频率降低到0.5～3 Hz。在任何载荷的作用下，橡胶空气弹簧都可以保持较低而近乎相等的振动频率。

研究结果表明，附加气室容积为主气室容积的2倍时，附加气室与空气弹簧间的节流孔由小变大过程中，可以使系统等效刚度降低60%左右，系统固有频率降低0.5～3 Hz，系统等效阻尼比呈现先增大后减小的趋势。附加气室容积的增大使得系统等效刚度和固有频率降低，但当附加气室容积大于主气室容积2～3倍后，附加气室容积的增大对系统的等效刚度和固有频率影响便不再明显。

另外，改变附加气室容积对系统的位移传递率、动载荷及响应加速度也具有显著的影响，在附加气室容积小于主气室容积2倍的范围之内时，附加气室容积的增大能够显著降低系统在共振频率点的位移传递率、加速度均方根值以及最大动载荷，但当附加气室容积超过主气室容积2倍时，附加气室容积的增大对以上3个指标的影响不再明显。

（2）簧囊橡胶材料本身刚度对系统一阶谐振频率的影响。试验证明，橡胶气囊材料本身刚度对空气弹簧刚度影响极大，这是造成空气弹簧刚度理论值与试验值差异较大的原因。橡胶气囊材料刚度越大，空气弹簧的刚度就越大，其一阶谐振频率越高，其结果提高了系统工作时最小工作频率。所以，橡胶气囊隔震系统应当减小材料刚度，减小自振频率，使得空气弹簧隔振器的承载能力留有足够的余量情况下，系统最小工作频率尽可能低。

（3）振动台横向振动时，簧囊橡胶材料刚度要大得多。橡胶空气弹簧的本体结构柔软，因此具有轴向、横向和旋转向的综合隔振作用。机械式振动台横向振动时，簧囊橡胶材料刚度要大得多。

（4）在空气弹簧和附加气室之间设一节流孔，当空气流过节流孔时，由于阻力而吸收一部分振动能量，从而起到减振阻尼的作用。除了影响系统的刚度和固有频率之外，节流孔的大小主要影响了系统的阻尼。

试验证明，系统刚度随节流孔开度增大而减小，阻尼随节流孔的增大先增大后减小，附加气室容积的增大能使系统刚度减小并使阻尼比增大，激励频率的增大会增大系统刚度并减小系统阻尼比，静载荷的变化对系统振动特性影响不大。

4 结束语

本文所述是一个针对机械振动台单自由系统中空气弹簧作为支撑时和减振隔振时系统的刚度和固有频率计算，实用性很强。

需要指出的是：文中的原理示意图及结构示意图是实际系统的简化，旨在说明原理，而并非是实际系统的复现。

[1]季文美，方同，陈松淇.机械振动[M].北京：科学出版社.1985.51-59.

[2]陈英会.弹簧[M].北京：机械工业出版社.1986.36-57.

[3]机械设计手册编委会.第二卷/机械设计手册（第3版）[M].北京：机械工业出版社.2004.