基于比例微分优化准则的拓扑优化方法

赵龙彪 高 亮 陈志敏 邱浩波

1．华中科技大学数字制造装备与技术国家重点实验室，武汉，430074 2．中国舰船研究设计中心，武汉，430064

0 引言

拓扑优化是在一个确定的区域内寻求满足设计约束的最优拓扑结构的优化方法。设计目标和约束可以为重量、频率、强度等。其主要求解思路是将寻求结构的最优拓扑结构问题转化为在给定的设计空间内寻求最优材料的分布问题［1］。它是一种能帮助设计者选择合适的初始拓扑结构的有效方法，在概念设计阶段具有十分重要的指导意义。

在拓扑优化的众多模型求解方法中，优化准则法（optimality criteria method，OC）［2］是根据满足各种约束条件（应力、位移、频率等）的最佳准则，从可行的设计中找出最佳方案的方法，以充分发挥材料的刚度、强度和稳定性的潜力，实现等强度、等应变能的最佳传导应力路径。最早的优化准则法包括互应变能法（constant mutual energy design）、应力比法（stress ratio method）和满应力法（fully stressed design）［3］。目前，学者们已经对OC法有了比较深入的探讨，Meske等［4］对OC法的健壮性和快速收敛性进行了研究，并应用在结构的固有频率优化上。Logo等［5］把OC法应用在随机拓扑优化设计问题上。Chiandussi等［6］把遗传路径加入到OC法中。

优化准则法的每一次迭代都是根据上一次迭代中各单元的材料密度和敏度信息，按照固定法则来计算各单元新的材料密度。在求解过程中，搜索效率不高，容易产生局部震荡和难以收敛的现象，会降低求解的速度。鉴于此，本文在传统OC法的基础上，基于SIMP密度函数插值模型，以结构的柔度最小化为目标函数，借助比例微分控制的思想，提出了比例微分优化准则法（proportional and differential optimality criterion method，PDOC），改进了迭代算子，给出了设计变量的迭代更新方案。在提高搜索效率的同时，加快了优化速度，并使得求解更容易收敛。

1 结构拓扑优化设计基础

1.1 结构拓扑优化模型

结构拓扑优化的目的是确定设计域中材料的最优分布。为实现材料的最优分布，需要进行材料密度的连续化插值。变密度法是人为假定单元的密度和材料物理属性（如许用应力、弹性模量）之间的某种对应关系，以连续变量的密度函数形式显式地表达这种对应关系。变密度法主要的密度－刚度插值方式有带惩罚指数的固体各向同性微结构模型SIMP［7］和材料属性的理性近似模型RAMP［8］两种，本文以SIMP模型为例讨论连续体结构拓扑优化模型。

SIMP模型主要通过引入惩罚因子，在材料的弹性模量和单元相对密度之间建立起一种显式的非线性对应关系。其目的是当设计变量的值在（0，1）之间时，对中间密度值进行惩罚，使其逐渐向0／1两端聚集，这样可以使连续变量的拓扑优化模型能很好地逼近原来0－1离散变量的优化模型。

SIMP材料模型的数学表达形式：

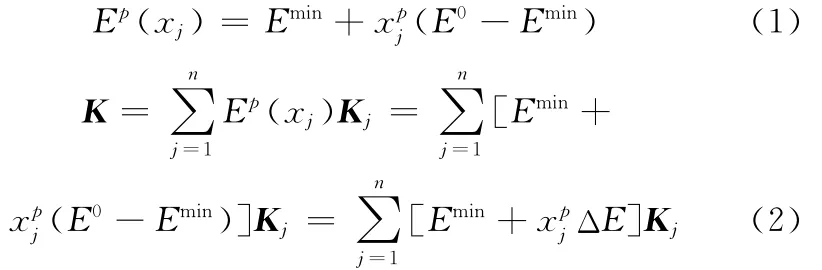
式中，xj为一般设计变量，表示离散单元的相对密度；p为SIMP模型中对中间密度材料的惩罚因子；E0、Emin分别为固体和空洞部分材料的弹性模量；Ep为插值后的弹性模量；K为插值以后的刚度矩阵；Kj为第j个单元固体材料的刚度矩阵。

惩罚因子的作用是当设计变量的值在［0，1］之间时，通过逐渐增加p的值对设计变量的中间值进行惩罚，随着p值的增大，设计逐渐接近0／1设计。为有效压缩中间密度材料，要求p＞2［9］。结构拓扑优化过程中，通过不断地优化迭代计算，来保留对结构传力路径有利的单元，删除对结构传力路径作用不大的单元，从本质上讲，结构拓扑优化问题是一个单元集合的增减问题。对于连续体拓扑优化模型，对每个单元j的增减操作变成对xj（j＝1，2，…，n）值的加减操作，并且使其值在［0，1］之间变化。

以结构拓扑优化中比较典型的最小柔度问题为例，在SIMP材料插值方法的基础上，拓扑优化模型为

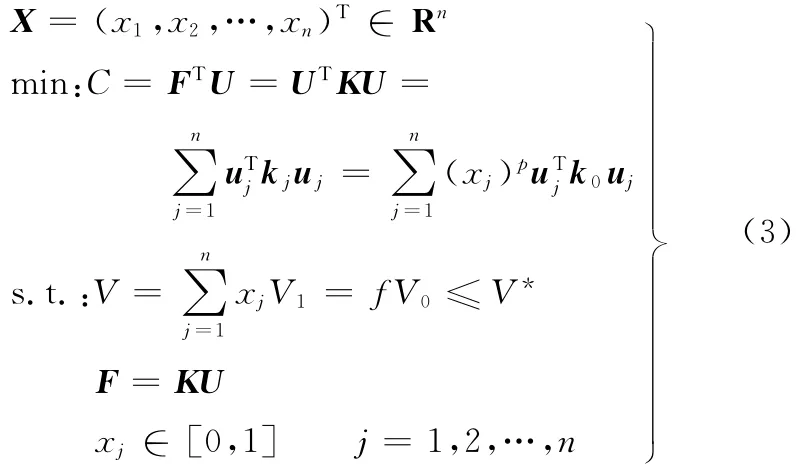
式中，C为目标函数，定义C为结构的总体柔度；F为单元载荷矢量；U为单元位移列阵；K为结构总体刚度矩阵；V1为每个单元的设计域的初始体积；V0为设计域的初始体积；V为优化后的结构体积；f为优化体积比；uj为单元位移列向量。

1.2 优化准则法

优化准则法（OC）是根据工程经验、力学概念以及数学规划的最优条件，预先建立某种准则，通过相应的迭代方法，获得满足这一准则的设计方案，作为问题的最优解的一种优化方法。在实际运用中，OC法可以并行处理设计空间的所有单元，快速地发现应力传递的主要路径，能够求解超大规模设计变量的拓扑优化问题。

优化准则法中应用最成功的是Kuhn－Tucker条件。下式所示的是不等式约束的多元函数极值问题，其中X＝ （x1，x2，…，xn）T为设计变量，受到m个不等式约束。

拓扑优化问题是典型的不等式约束的多元函数极值问题，它通过Kuhn－Tucker条件构造多元函数的极值条件函数，通过求极值条件函数间接求多元函数的极值点。优化准则法从一个空间的初始设计点x（k）出发，着眼于每次迭代应满足的优化条件，依据迭代式：

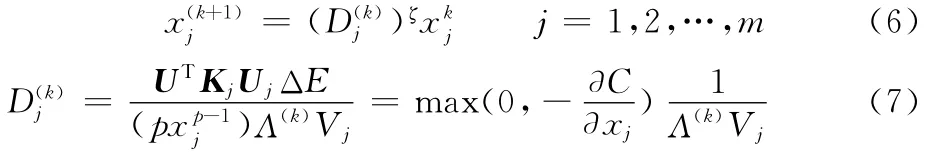
式中，ζ为阻尼因子（0＜ζ＜1）；k为迭代步数；Vj为体积比。得到一个改进的设计x（k＋1）。式（6）中常常引入一些经验系数来调整优化过程的收敛性和稳定性，如步长因子、阻尼因子等。

总体来讲，OC法简单明了、易于理解，但其设计变量更新来源于一种启发式的迭代方式，在实际的应用中还存在着一些缺陷：

（1）设计变量的更新通过预定的迭代控制策略进行搜索，总是按照预先规定的路线进行，这种搜索具有盲目性，效率不高，会降低求解速度。

（2）求解通用性较差，对于复杂的目标函数，不容易构造设计变量的迭代公式，搜索过程中的指导信息只有当前结果和目标结果的偏差，所以容易出现震荡和难以收敛的现象。

（3）一般比较适用于单目标函数、单约束条件下的优化问题求解，多目标问题需要推导不同的优化准则，难以适用于复杂问题的求解。

针对这些情况，我们在OC法的基础上，通过引入比例微分控制（PD）的思想，改进其迭代算子，并给出设计变量的迭代更新方案，提出了PDOC方法，并将其用于拓扑优化中，以求在传统OC法优势基础上，进一步加快收敛，提高求解速度，改善优化效果。

2 PDOC方法及算法实现

2.1 PD控制基础

其思想来源于工程控制中广泛应用的比例、积分和微分控制方法，简称PID控制。PID控制在实际中又可以根据情况简化为PI控制和PD控制。

（1）比例控制（proportional control）。比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系，可适当缩放信号的幅值。控制器中，比例项的引入，能够放大误差的幅值。

（2）微分控制（differential control）。在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。控制器中，微分项的引入，能够预测误差变化的趋势。

（3）比例微分控制（proportional and differential control）。单一的比例控制或者微分控制都不能完全解决问题，只有同时具有比例、微分控制的控制器，才能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免被控量的严重超调。

因此，对有较大惯性或滞后的被控对象，比例微分（PD）控制器能改善系统在调节过程中的动态特性，通过引入比例项，放大误差的增幅；增加微分项，便能预测误差变化的趋势。这样，具有比例、微分环节的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。

2.2 PDOC方法介绍

传统OC法迭代公式计算简单、易于数值实现，但其收敛速度不够。在实际的数值试验中，为加快迭代法的收敛速度，可以通过多级定常迭代的思想构造迭代公式，如：

即在计算x（k＋1）时考虑前面l个迭代值，这样的迭代法称为l级定常迭代法。如果φk与k无关，迭代公式可表达成以下形式：

多级迭代法在数值计算过程中比单级迭代法需要保存更多的信息，增加了存储量。所以一般l不宜太大，常在计算x（k＋1）时考虑前面2个迭代式。迭代式如下：

在实际优化问题中，求解的非线性方程组结构复杂，很难通过确切的数学推导过程构造二级定常迭代法。这与控制系统中的很多情况类似，我们可以把x（k＋1）看作是控制系统φ（x（k），x（k－1））的输出变量，而x（k），x（k＋1），…，x（k－l＋1）为控制系统的输入变量。控制系统φ（x（k），x（k－1））是一个黑匣子，无法得知其内在的控制机理。在控制工程中，当被控对象的结构和参数不能完全明确，或得不到精确的数学模型，而控制理论的其他技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时最适合应用PD控制方法。PD控制器就是根据系统的误差，利用比例、微分计算出控制量进行控制的。输入误差信号可以用差分形式表达如下：

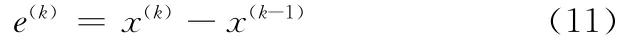
结合优化准则迭代方法和微分控制的思想，可以构造比例微分迭代公式如下：

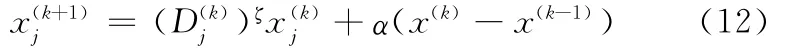
式中，α为微分项的影响因子，简称微分参数。

称这种结合优化准则迭代方法和微分控制思想的二级定常迭代法为PDOC方法。

考虑迭代算子的移动极限和收敛效果，可以把迭代算子改进为

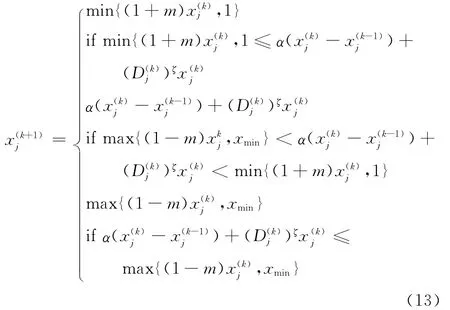
式中，m为移动极限（0＜m＜1）；ζ为阻尼因子（0＜ζ＜1）；xmin为材料密度的下限值，xmin＝0．0001；Λ 为拉格朗日乘子。

在每一步迭代中，确保体积约束满足的拉格朗日乘子Λ是变化的，在第k步，可以采用二分法求解Λ：

（4）重复步骤 （2）和 步骤 （3），直到满 足｜V（k）－V＊｜≤δ（δ＝0．0001）。

2.3 PDOC算法实现

图1为基于PDOC法拓扑优化设计的算法流程图，可以采用 MATLAB实现算法，步骤如下：

（1）有限元模型的前处理，主要包括网格划分、定义约束和载荷。

（2）初始化设计变量，定义单元的初始材料密度，默认的值均为0．5。

（3）有限元分析求解，计算出各单元的敏度和刚度，并进行敏度分析与过滤。

（4）根据上一步迭代更新的各单元材料密度，采用PDOC法计算各单元新的材料密度和结构柔度。

（5）判断是否达到优化设计目标。如果未达到优化设计目标，则转步骤（3）继续优化；如果达到优化设计目标，则转步骤（6）。一般终止设计目标有两种情况：一是材料密度总和达到最小约束界限；二是结构的整体柔度值的改变量达到预定界限。

（6）输出结果，结束。

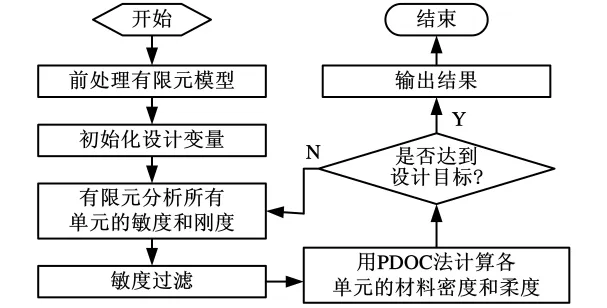
图1 PDOC法拓扑优化求解流程图

3 实例分析

3.1 悬臂梁刚度优化

图2所示为悬臂梁刚度优化问题的设计域示意图，其设计空间长A＝60mm，高B＝20mm。材料的弹性模量为207GPa，泊松比为0．3，体积比为0．5。结构左侧的竖边受X和Y方向的自由度约束，右侧中间位置受垂直向下的10kN载荷作用。

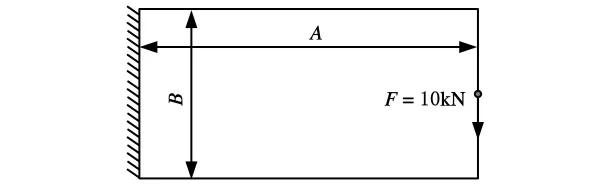
图2 悬臂梁柔度最小化问题的设计域示意图

首先通过试验分析PDOC法中的微分参数对求解效果的影响。试验电脑CPU主频率为2．0GHz，内存为2GB。采用MATLAB语言实现算法。

网格划分为120×40，单元数为4800。分析式（12）可知，当α≠0时，即为PDOC方法，当α＝0时，PDOC方法即退化为OC法。经过测试发现，实际求解过程中，一般取0．5＜α≤0．9时，求解效果较好。为比较PDOC法与OC法的求解效果，我们仅取α＝0和α＝0．8作为典型代表进行对比分析。求解结果如图3所示，解的柔度进化曲线如图4所示。从求解结果可以看出，当采用PDOC法求解时，求解过程均比较稳定，经过10步迭代就能接近最优值173．68，每步迭代耗13．673s。当采用OC法求解时，大概需经过20步迭代才能接近最优值，每步迭代耗13．452s。从优化过程看，PDOC法比OC法有更快的收敛速度，更容易收敛；从优化结果看，PDOC法比OC法能获得刚度更大的结构，在加快收敛的同时，提高了结构刚度。

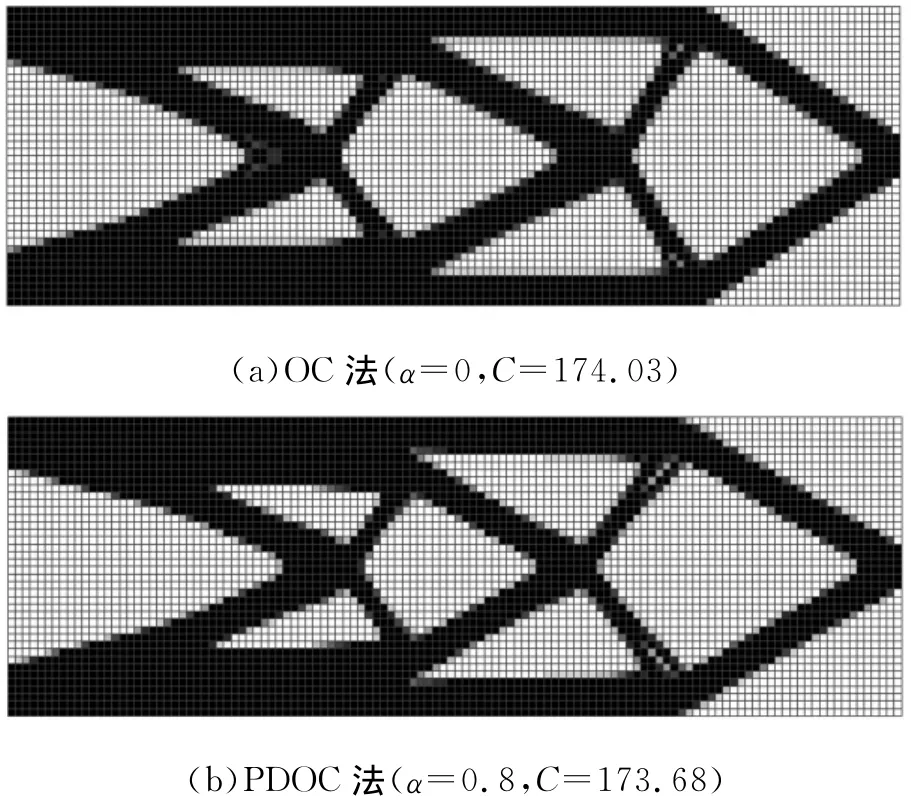
图3 网格划分120×40悬臂梁的解

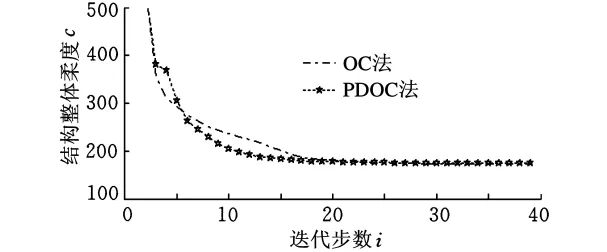
图4 网格划分120×40的悬臂梁柔度进化曲线比较图

3.2 简支梁刚度优化

如图5所示的简支梁刚度优化问题的设计域示意图，其设计空间长A＝240mm，高B＝40mm。材料的弹性模量为207GPa，泊松比为0．3，体积比为0．5。中间位置受垂直向下的10kN载荷作用。试验电脑CPU主频率为2．0GHz，内存为2GB，采用 MATLAB语言实现算法。

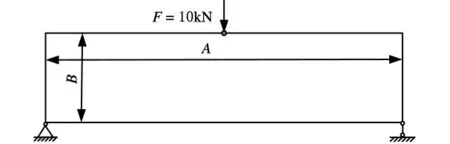
图5 简支梁柔度最小化问题的设计域示意图

设定网格划分为240×40，单元数为9600。惩罚因子p＝3，体积比V＊＝0．5，阻尼因子ζ＝0．5，移动极限m＝0．3，最大迭代步数为40。

求解结果如图6所示，解的柔度进化曲线如图7所示。从求解结果可以看出，当采用PDOC法求解时，求解过程均比较稳定，经过15步迭代就能接近最优值192．15，每步迭代耗14．792s。当采用OC法求解时，大概需经过25步迭代才能接近最优值，每步迭代耗14．358s。从优化过程看，PDOC法比OC法有更快的收敛速度，更容易收敛；从优化结果看，PDOC法比OC法能获得刚度更大的结构，在加快收敛的同时，提高了结构刚度。

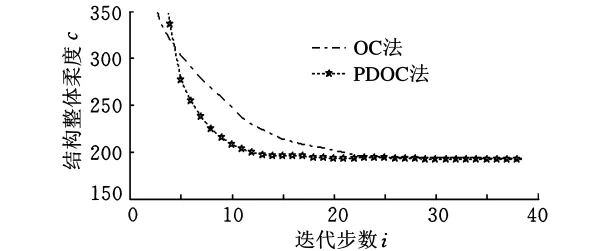
图7 网格划分240×40的简支梁柔度进化曲线比较图

3.3 柔性位移反向器

柔性机构是通过其部分或全部具有柔性的构件变形而产生位移的机械结构，它的设计主要要求在输入端施加输入载荷以后，在输出端产生位移运动。柔性机构是多目标设计问题，优化的两个目标函数分别为机构的共有应变能（mutual strain energy，MSE）和结构的应变能（strain energy，SE）［10］。

本文以位移反相器的拓扑优化为例，验证PDOC方法的求解性能。拓扑优化的两个目标函数分别是最大化输出端的MSE以及最小化结构的SE。设计的体积比为30%。设计域尺寸为80μm×80μm，如图8所示。利用对称性，选取设计域的上半部分进行分析。在上半部分均布80×40个网格。材料弹性模量为1MPa，泊松比为0．3，输入驱动力为fin＝0．5mN，uout为输出位移。在输入端口固定一个刚度为Kin＝1的弹簧，输入能量通过输入驱动力和弹簧的刚性来表示。在输出端固定一个刚度为Kout＝1的弹簧来模拟工件对机构的作用力。

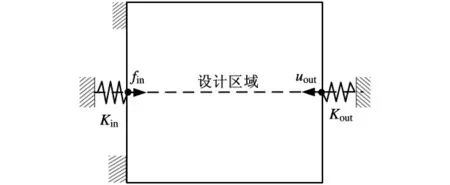
图8 位移反相器的设计域示意图

求解结果如图9所示，解的MSE进化曲线如图10所示。从求解结果可以看出，当采用PDOC法求解时，求解过程均比较稳定，经过15步迭代就能接近最优值MSE＝0．821 45，每步迭代耗9．876s。当采用OC法求解时，大概需经过40步迭代才能接近最优值MSE＝0．789 46，每步迭代耗9．435s。从优化过程看，PDOC法比OC法有更快的收敛速度，更容易收敛；从优化结果看，PDOC法比OC法能获得刚度更大的结构，因此，在多目标问题的拓扑优化求解中，PDOC方法仍然具有较好的实际应用效果，在加快收敛的同时，提高了结构刚度。

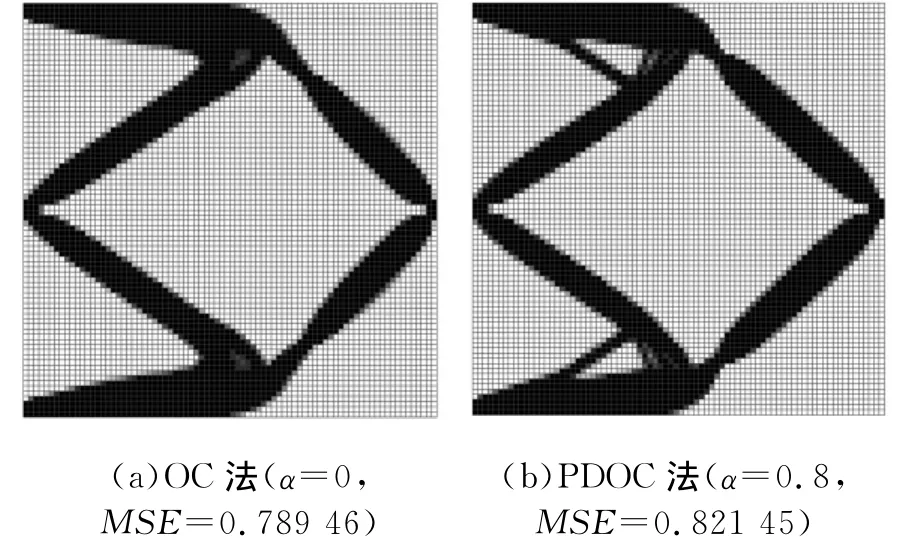
图9 位移反相器简支梁的解

图10 位移反相器MSE进化曲线比较图

4 结语

本文在PD控制理论的基础上，提出了基于PDOC的拓扑优化方法。PDOC法通过引入比例微分控制的思想来改进迭代算子，通过构造更合理的数值迭代公式以加快收敛，提高计算速度。引入比例、微分控制的求解算法，以预测误差的变化方向，提前抑制误差的作用，从而避免了被控量的超调现象和震荡现象，经过实例测试，采用改进后的PDOC方法进行拓扑优化，能够使优化求解过程经过10次左右迭代就能收敛，明显比OC法的搜索速度要快，同时还能够求出柔度更小且结构更清晰的解。另外，通过一个多目标优化实例测试，验证了PDOC方法在多目标拓扑优化问题求解中的有效性。综上所述，PDOC方法是一种比OC方法求解速度更快、求解结果更好的方法。

［1］ 罗震，陈立平，黄玉盈，等．连续体结构的拓扑优化设计［J］．力学进展，2004，34（4）：463－476．

［2］ Zhou M，Rozvany G I N．The COC Algorithm，Part II：Topological Geometrical and Generalized Shape Optimization［J］．Computer Methods in Applied Mechanics and Engineering，1991，89：197－224．

［3］ Levy R，Lavan O．Fully Stressed Design of Passive Controllers in Framed Structures for Seismic Loadings［J］．Structural and Multidisciplinary Optimization，2006，32（6）：485－498．

［4］ Meske R，Lauber B，Schnack E．A New Optimality Criteria Method for Shape Optimization of Natural Frequency Problems［J］．Structural and Multidisciplinary Optimization，2006，31（4）：135－140．

［5］ Logo J．New Type of Optimality Criteria Method in Case of Probabilistic Loading Conditions［J］．Structural and Multidisciplinary Optimization，2007，35（2）：147－162．

［6］ Chiandussi G，Codegone M，Ferrero S．Topology Optimization with Optimality Criteria and Transmissible Loads［J］．Computers and Mathematics with Applications，2009，57：772－788．

［7］ Rietz A．Sufficiency of a Finite Exponent in SIMP（Power Law）Method［J］．Structural and Multidiscipline Optimization，2001，21：159－163．

［8］ Stolpe M，Svanberg K．An Alternative Interpolation Scheme for Minimum Compliance Topology Optimization［J］．Structural and Multidiscipline Optimization，2001，22：116－124．

［9］ 罗震，陈立平，黄玉盈，等．基于RAMP密度－刚度插值格式的结构拓扑优化［J］．计算力学学报，2005，22（5）：585－590．

［10］ Frecker M，Ananthasuresh G K，Nishiwaki S，et al．Topological Synthesis of Compliant Mechanisms Using Multi－criteria Optimization［J］．Mech．Des．Trans．ASME，1997，119（2）：238－245