两个不同结构六相永磁同步电机串联驱动系统
苗正戈, 刘陵顺, 张海洋
(1.海军航空工程学院研究生大队,山东 烟台 264001;
2.海军航空工程学院控制工程系,山东 烟台 264001)
0 引言
随着电力电子技术的发展,电机的相数可以摆脱单相或三相的束缚成为一个自变量。与传统的电机相比,主要有以下优点:在供电电压受限制的场合,采用多相电机是解决大功率的有效方案;相数增加,转矩脉动减小、脉动频率增加,低速特性得到很大改善,振动和噪声减小;由于相数增加,驱动系统的可靠性大大提高。在实际应用方面,早在1982年,欧洲科学家T.M.Jahns已经将15相电机应用在潜艇驱动系统。多台电机系统在日常生活中应用更加广泛,但多台多相电机串联驱动系统的研究是最近几年才兴起的课题。多台电机由单一逆变器供电,主要具有以下特点:减少了逆变器支路数量,提供了直接利用制动能量的可能;这方面的研究成果主要集中在Emil Levi所领导的课题组,阿尔及利亚大学的A.DIAHBAR等人对Emil Levi的工作进行了深入研究,但是他们的研究对象都是多相感应电机,对永磁同步电机 (Permanent Magnet Synchronous Motor,PMSM)串联驱动系统的研究,至今仍是空白。本文则主要对PMSM的串联系统进行研究,通过对两台串联PMSM工作原理进行分析,确定串联驱动系统的动态解耦性。
1 两PMSM串联驱动系统分析
1.1 对称六相PMSM 和夹角为0°六相 PMSM串联方法
夹角为0°六相PMSM的重合绕组互感系数M=1,即 Mad=1,Mbe=1,Mcf=1,而 a相、b 相、c相之间分别成夹角120°,定子绕组分布情况如图1所示。
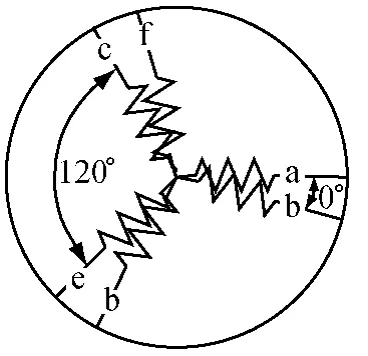
图1 夹角为0°六相PMSM定子绕组
对称六相PMSM绕组如图2所示,各相绕组间夹角相等,为 θ1=60°。

图2 对称六相PMSM定子绕组
多台电机串联到一起,且能够实现独立控制的条件是:一台电机的磁通和转矩生成电流在其他电机中不产生磁通和转矩,简单地将定子串联显然不满足条件,所以需要引入相序转换,这样可以把自然坐标下的电机变量(相电压、相电流等)变换到dq-z1z2-o1o2新参考坐标系下,dq子空间中的基波及谐波将在电机中形成旋转磁动势,与电机的机电能量转换相关;z1z2子空间与dq子空间正交,该子空间的谐波在绕组正弦分布的电机中不形成旋转磁动势,与电机的机电能量转换无关,只在定子绕组上感应出谐波电流,可以称为广义的零序分量;o1o2定义为零序子空间,它们与dq和z1z2子空间都正交,对于星形联接的没有中点的多相电机中,o1o2子空间的零序分量不存在。
本课题就是致力于研究定子绕组正弦分布时一台多相电机的z1z2零序子空间中的变量构成另一台与其串联的多相电机的磁通和力矩来源,从而实现两台多相电机在同一个逆变器驱动下的独立运行,具体连接如图3所示。
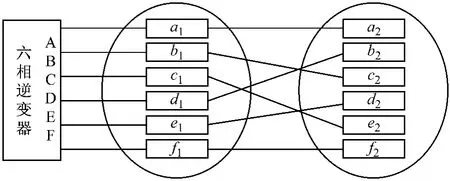
图3 两电机定子绕组连接图
1.2 转换矩阵
为了实现两台电机在同一逆变器下的独立运行,六相PMSM和夹角为0°六相PMSM串联转换矩阵如式(1)所示[3]:

经过[T]变换后的方程是静止状态两维坐标系下的方程,方程中含有转子的旋转角θr,要通过旋转变换消去θr,旋转变换矩阵为式中:θr——电机的转子角度。

2 串联系统数学模型

式中:us——逆变器电压;
us1——电机1每相定子绕组电压;
us2——电机1每相定子绕组电压;
rs1——电机1定子绕组电阻;
rs2——电机2定子绕组电阻;
Is——串联系统输入端的输入电流;
Ls1——电机 1 定子电感,Ls1=Lsσ1E+
由图3可知:Lsm1M1;
Ls2——电机 2 定子电感,Ls2=Lsσ2E+Lsm2M2;
Lsσ1,Lsσ2——两电机每相的漏感;
Lsm1,Lsm2——两电机主磁通电感;
Ψsr1,Ψsr2——两电机转子磁场在定子绕组
中产生的磁链。
经广义两相实变换得:
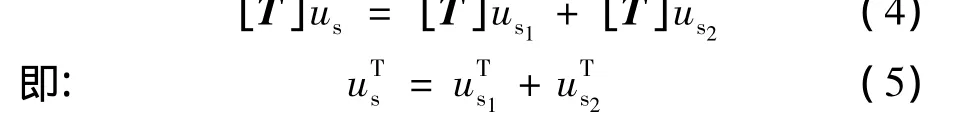
式(5)经旋转变换矩阵[R]得:
第一台电机在旋转坐标系d-q下电压电流关系式为
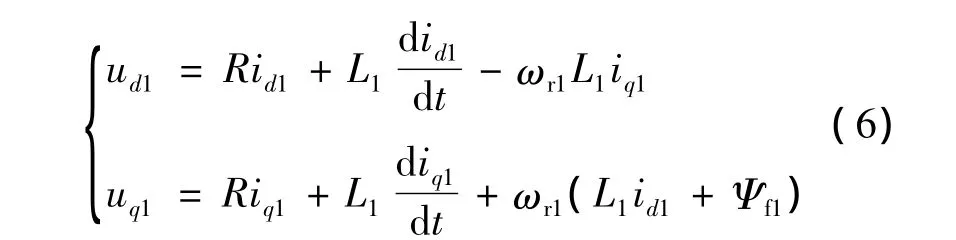
其中:R=rs1+rs2;
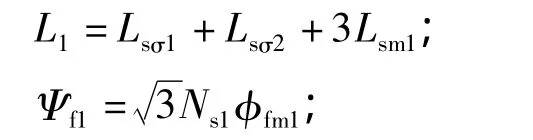
φfm1——第一台电机永磁体主磁路;
Ns1——第一台电机定子匝数;
ωr1——第一台电机转子转速。
转矩方程为
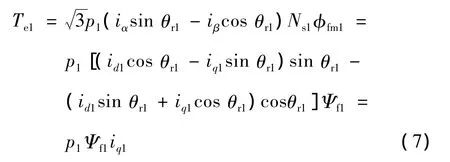
式中:p1——第一台电机极对数;
θr1——第一台电机转子磁链与定子A相的
夹角。
第二台电机在旋转坐标下电压电流关系式:
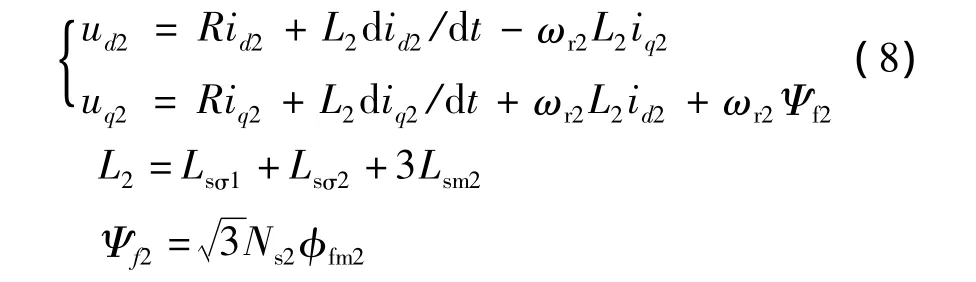
式中:φfm2——第二台电机永磁体主磁路;
Ns2——第二台电机定子匝数;
ωr2——第二台电机转子转速。
转矩方程:
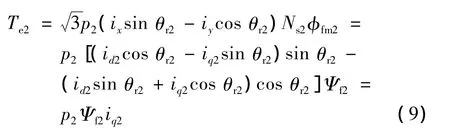
式中:p2——第二台电机极对数;
θr2——第二台电机转子磁链与定子A相的夹角。
运动方程如下:
第一台电机运动方程为

式中:J1、F1、Tl1、ωr1——第一台电机的转动惯量、转动摩擦系数、负载、转速。
第二台电机运动方程为

式中:J2、F2、Tl2、ωr2——第二台电机的转动惯量、转动摩擦系数、负载、转速。
对称六相PMSM与夹角为0°六相PMSM串联系统在MATLAB/Simulink环境下的仿真模型[4]如图 4 所示。
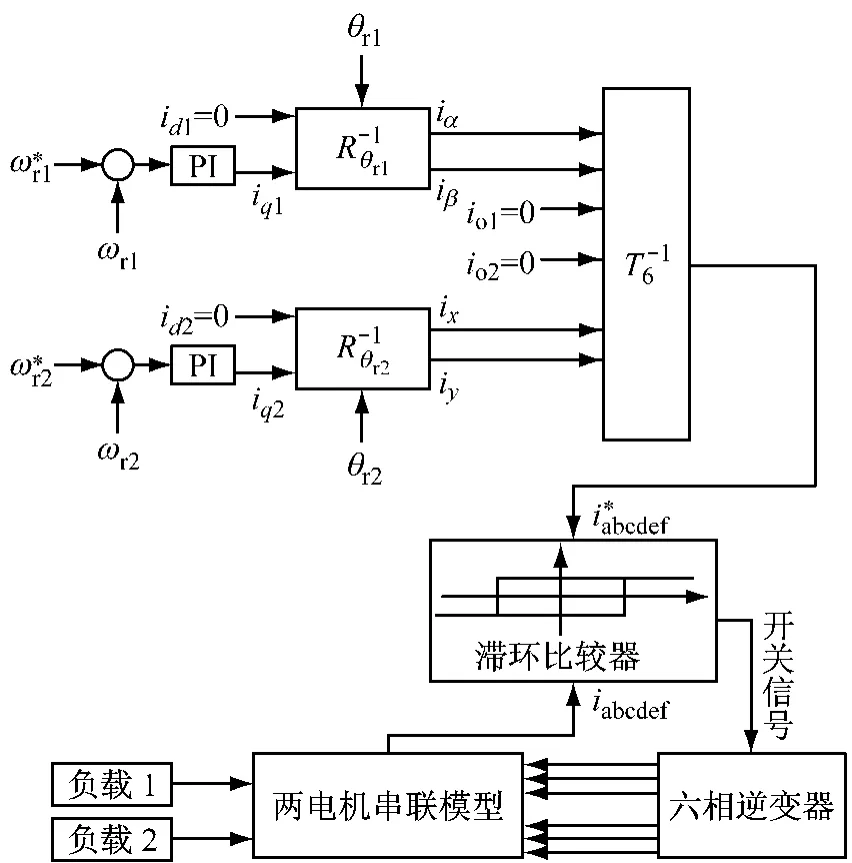
图4 矢量控制的两电机串联结构图
3 串联系统变载仿真分析
在上述Simulink仿真中,逆变器采用电流滞环比较控制方式,电机采用id=0的矢量控制方法。电机基本参数设置如下:R=2.875 Ω,p1=p2=4,Ψf1=0.175 Wb,Ψf2=0.2 Wb,L1=0.008 H,L2=0.013 H,J1=0.089 kg·m2,J2=0.1 kg·m2,F1=0.005,F2=0.01。
两个电机解耦的具体表现就是,当其中的一台电机转速发生改变时,对另外一台电机的转速、转矩等量没有影响。因此,设定电机转速按照如下规律变化:当 t=0 s时,电机 1的转速为300 r/min,并在整个过程中保持不变;当t=0 s时,电机2 的转速为400 r/min,在 t=0.6 s时,转速变为200 r/min。在整个过程中,负载1和负载2幅值设为零,两台电机转速、设定电流、输出电流和转矩的工作情况如图5~图6所示。
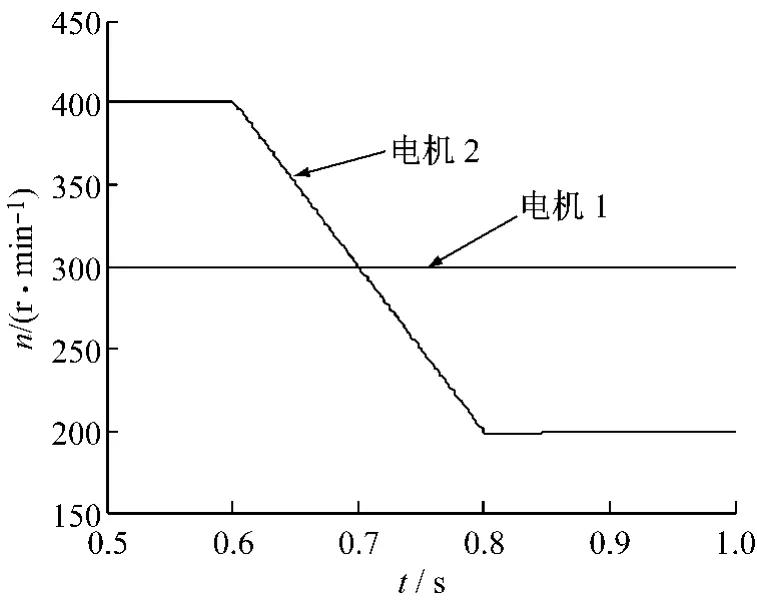
图5 时间-转速曲线
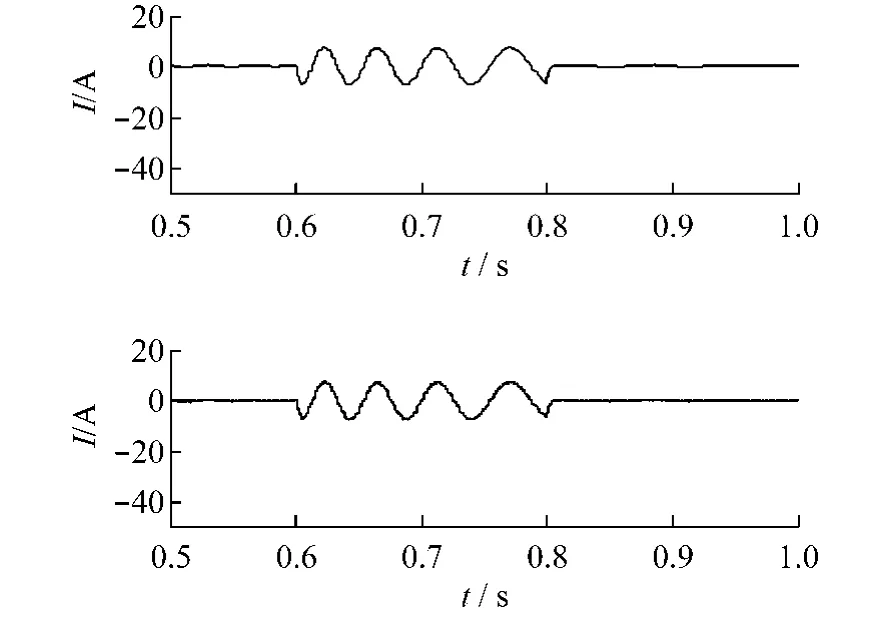
图6 电流曲线
通过仿真图像,当电机2的转速在t=0.6 s由400 r/min变为200 r/min时,电机2的转矩相应发生变化,但是,电机1的转速和转矩始终没有变化,逆变器输出电流能很好地跟踪设定电流。
将上述条件变为:当t=0~1 s过程中,两电机转速保持不变,分别保持电机1转速在300 rad/s,电机2的转速保持在200 rad/s,在t=0.4 s时电机1的负载值变为10 N·m,在 t=0.37 s电机2负载值变为8 N·m,仿真结果如图7~图9所示。
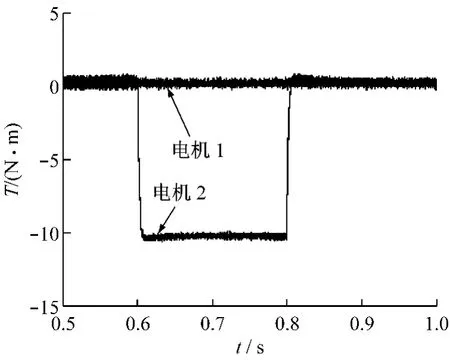
图7 时间-转矩曲线
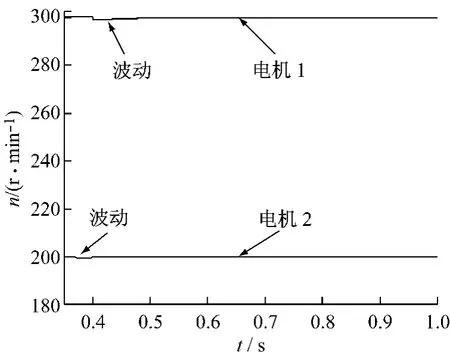
图8 时间-速度曲线
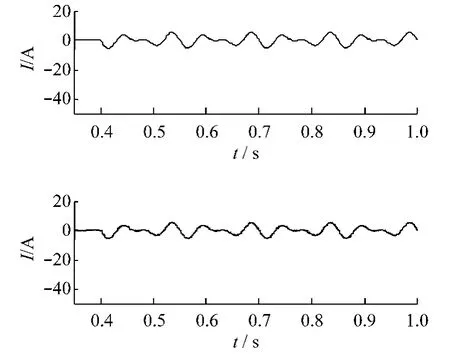
图9 电流曲线

图10 时间-转矩曲线
通过仿真可知,在t=0.37 s和t=0.4 s时,两负载分别作用于两个电机,两电机速度曲线在经历短时间的波动后恢复到原来数值,说明系统有抵抗外界干扰的能力,同时输出电流能很好地跟踪设定电流。两台电机在达到稳定状态时,分别对应相应的转矩输出,并且从转矩曲线可以看出,两电机分别独立对系统的负载作出反应,从而证明了两串联电机实现了解耦。
4 结语
通过上述分析,可以得到以下结论:
(1)电机2转速变化对电机1没有影响,两台电机转速可以实现独立控制。
(2)滞环控制器能够保证逆变器实际输出电流很好地跟踪设定电流,电流响应速度快。
(3)两电机的转矩和负载变化没有相互影响,从而说明两台电机在运行时实现了解耦。
由以上分析可知,两电机这种连接方法和控制方式,实现了两台电机解耦,同时论证了对称六相PMSM串联三相PMSM的可行性。
[1]Emil Levi,Martin Jones,Slobodan N,et al.A novel concept of a multipase multimotor vector controlled drive system supplied from a single voltage source inverter[J].IEEE Trans on Power electronics,2004,19(2):320-325.
[2]薛山,温旭辉.基于矢量空间解耦的五相永磁同步电机建模与仿真[J].微特电机,2006,10(6):21-26.
[3]陈菊明,刘峰,梅生伟,等.多相电路坐标变换的一般理论[J].电工电能新技术,2006,25(1):44-48.
[4]陈林.感应电机空间电压矢量选择与控制研究[D].武汉:华中科技大学,2003.
[5]Djahbar A,Mazari B,Mansour N.A novel concept for multimachine drive systems with rotor time constant estimation[C]∥International Multi-Conference on Systems,Signals and Devices,2008:1081-1085.

