基于三电平逆变器供电的电机直接转矩控制系统

潘 登，任 冲，柴文野，张 震

(安徽理工大学电气与信息工程学院，安徽淮南 232001)

0 引言

直接转矩控制(Direct Torque Control，DTC)是直接利用逆变器输出的电压矢量控制定子磁链及电磁转矩的控制方法。目前在DTC系统中，两电平的三相交－直－交电压型逆变器得到广泛使用，该逆变器具有结构简单、控制理论成熟等优点，但两电平逆变器在空间上只输出互差60°电角度的6个运动矢量和2个零矢量，而且这6个运动矢量的幅值也不变，所以从根本上来讲，两电平逆变器对定子磁链矢量的旋转控制精度十分有限。

三电平逆变器供电的DTC系统，能输出多种幅值和相位的电压矢量，能够控制定子磁链的多种变化率，本质上能实现定子磁链矢量在空间上以多方向、多变化率的控制，有效解决了DTC系统中转矩脉动、磁链脉动较大等问题。

1 三电平逆变器工作原理

三电平逆变器的拓扑主要有两种，即二极管钳位式三电平逆变器和飞跨式三电平逆变器，图1给出二极管钳位式三电平逆变器的主电路图。在三电平逆变器中，每一相需要4个主功率器件、4个续流二极管、2个钳位二极管，平均每个主开关所承受的正向电压为Udc/2。每相桥臂的4个功率器件串联，直流电路中性点由2个钳位二极管引出，分别接到上、下桥臂的中间，使每个功率器件的耐压值减小到原来耐压值的1/2，有效保护了电路结构中的各种电力电子器件。

逆变器稳定工作有三种工作状态，由于三相原理相同，故针对A相给出说明。当VT1、VT2导通，VT3、VT4关断时，若负载电流为正方向，即电流从P点经过VT1、VT2到达负载，此时输出端电位为Udc/2;若负载电流为负方向，电流由VT1、VT2反并联的二极管VD1、VD2流回P点，输出端电位仍为 Udc/2。当 VT2、VT3导通，VT1、VT4关断时，若负载电流为正方向，则电流从中性点O通过钳位二极管、主功率器件VT2到达负载，且输出点的电位与中性点相同;若负载电流为负方向，电流从输出端流过VT3、钳位二极管注入中性点，输出端电位仍与中性点相同。当VT3、VT4导通，VT1、VT2关断时，若负载电流为正方向，电流由N点经过VT3、VT4反并联的二极管VD3、VD4流向负载，此时输出电压为－Udc/2;若负载电感续流完毕，电流开始反方向流动时，其经过VT3、VT4流回N点，输出电压仍为 －Udc/2。由此可得，在中性点钳位的逆变器中，主开关VT1、VT4是不能同时导通的，而VT1和VT3、VT2和VT4是刚好互补的。

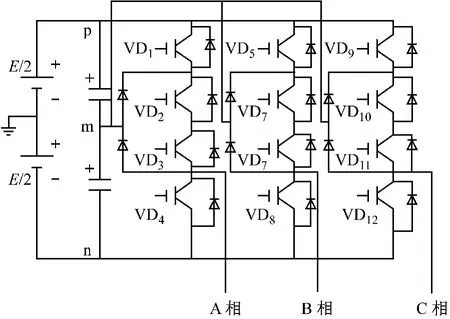
图1 三电平逆变器电路图

图2 三电平逆变器电压矢量图

三电平逆变器具有27种开关组合，每一种开关组合对应输出一种电压矢量，图2给出了三电平逆变器的电压矢量图。从图中可以看出，它不仅包含了两电平逆变器的6个电压矢量u1～u6(002、020、022、200、202、220)，而且其内六边形的每一个空间矢量对应着两个可能的开关状态，三电平逆变器输出电压矢量可以有四种幅值，即0、，这样定子磁链的变化率就有4种，因此能够更好地实现磁链矢量在空间上以多方向、多变化率进行控制。

2 三电平逆变器供电的DTC策略

三电平逆变器供电的DTC系统利用逆变器输出的电压矢量控制定子磁链及电磁转矩。它通过检测定子电压和电流矢量，直接计算出电机的磁链与转矩，并与磁链和转矩的额定值进行比较，实现对定子磁链和转矩的解耦控制。

图3给出了三电平逆变器供电的DTC系统结构图。图3中，DTC为磁链、转矩自控制单元;AFC为磁链观测器;ATC为转矩估计器;VSI为电压型的逆变器。

图3 三电平DTC系统基本结构

磁链观测器:

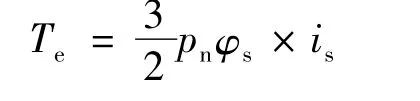
由转矩估计器观测的转矩Te与转矩给定值T*e进行比较，同时，磁链给定值φ*s与观测值φs

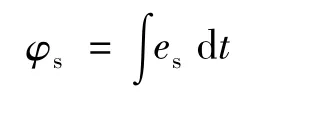
转矩估计器:进行比较，分别得到转矩与磁链的调节信号TΔ、φΔ，将两个调节信号送入磁链、转矩自控制单元，根据磁链旋转方向、磁链增加还是减少、转矩增加还是减少来选择适当的电压矢量，进而去选择变频器的开关模式，达到控制转矩和磁链的目的。

3 三电平逆变器供电的DTC模型

利用MATLAB 6.5对三电平DTC系统进行搭载，如图4所示，所用模块主要包括3/2变换、定子磁链观测器、转矩观测器、矢量发生器等。系统包括6个矢量发生器，分别用于大扇区的判断与角度输出、矢量重构、小区域的判断、各区域作用时间分段、电压矢量的选择、开关量的触发等。

图4中，磁通和转矩观测器输出三个信号:定子磁链矢量的幅值φsmax与相位角φω、实际的转矩观测值T，相位角信号φω用来选择扇区，再根据三电平的DTC矢量图决定在该扇区选择合适的电压矢量来控制磁场，实现多电平电压矢量的交替使用。幅值信号φsmax被送至磁链滞环比较器，与磁链给定值φ*smax进行比较，进而控制磁链幅值以及构造图形磁场。同时，转矩观测值T也被送至转矩滞环比较器与转矩给定值T*进行比较，决定合适的插入和撤销的零电压矢量。最后，将转矩选择、磁链选择、扇区选择结果送入开关选择环节，生成的脉宽调制(Pulse Width Modulation，PWM)控制信号，再去触发变频器对电机供电，实现变频及转矩控制。

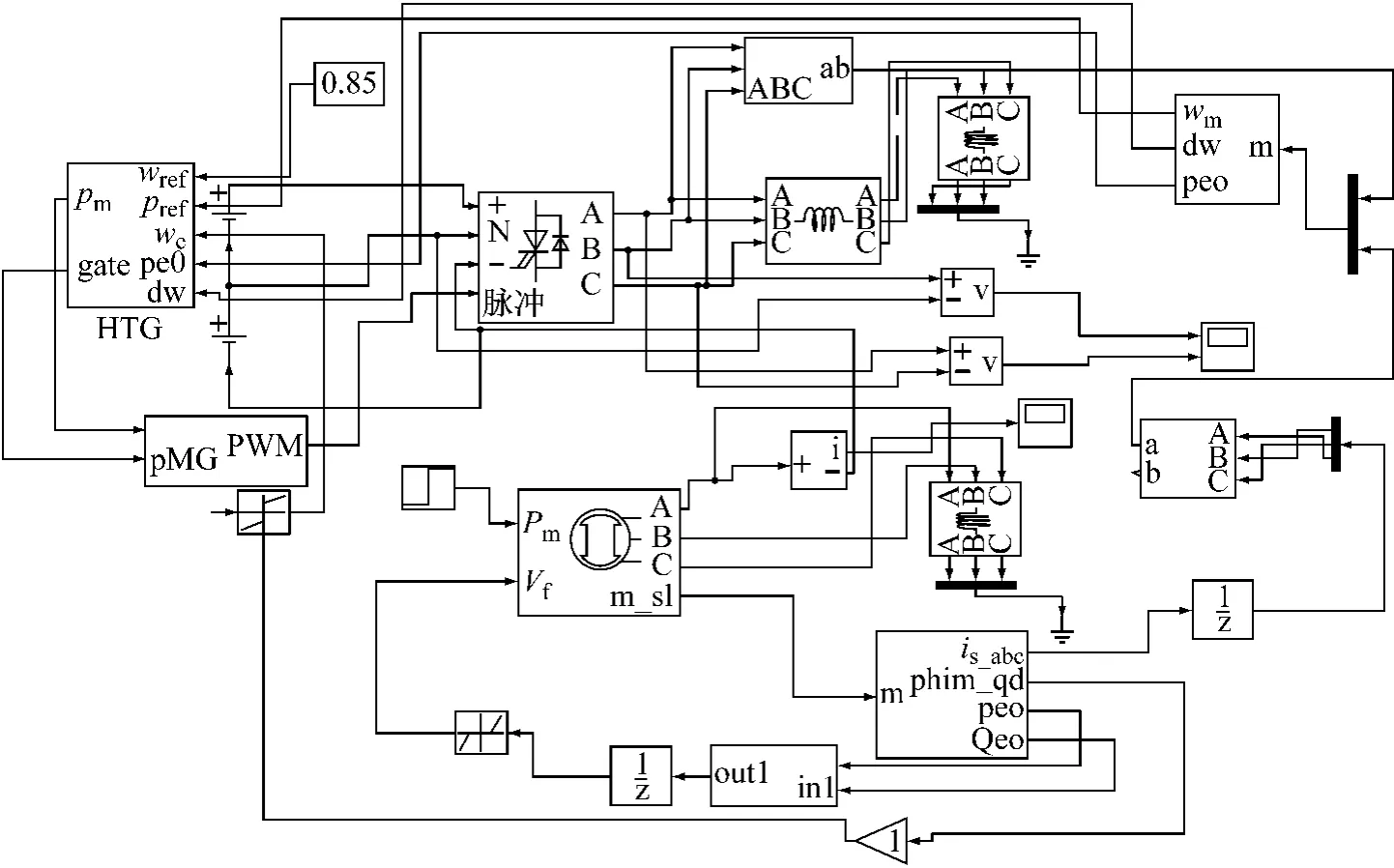
图4 三电平DTC模型搭建图

4 三电平逆变器供电的DTC系统仿真

对系统仿真参数作如下设定:定子电阻Rs=3.2 Ω，转子电阻 Rr=3.59 Ω，定子漏电感 L1s=0.027 3 H，转子漏电感 L1r=0.027 3 H，互感 Lm=0.622 2 H，转动惯量 J=0.12 kg·m2，电机极对数p=2;直流侧电容C1=C2=250 μF;控制周期为 100 μs;基波频率为 50 Hz。

图5与图6分别给出了三电平供电的交流电机负载条件下的转矩阶跃曲线与转速曲线图。图6中，在电机从起动到额定转速运行下，系统响应速度很快也较为平稳，转速的波形响应也很平稳。图5中在t=0.75 s时刻突加负载，电机负载由0 N·m阶跃为15 N·m，转矩有较小的脉动，但是可以很快平稳下来;在t=1.5 s时刻突减负载，电机负载由15 N·m阶跃为5 N·m，电机转矩稳定于额定值且转矩响应迅速;当电机负载变化时，系统无稳态误差，恢复时间小于0.1 s，负载转矩脉动非常小。这说明，基于三电平逆变器供电的DTC系统具有良好的动态性能和稳态性能。

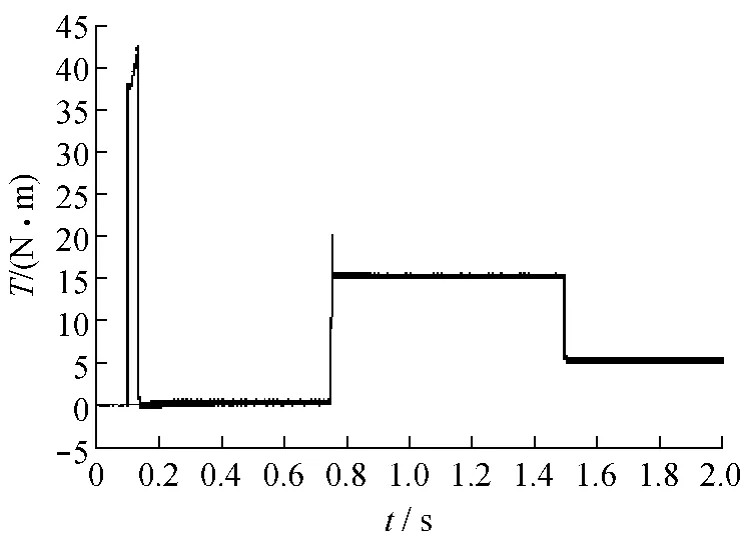
图5 电机转矩波形

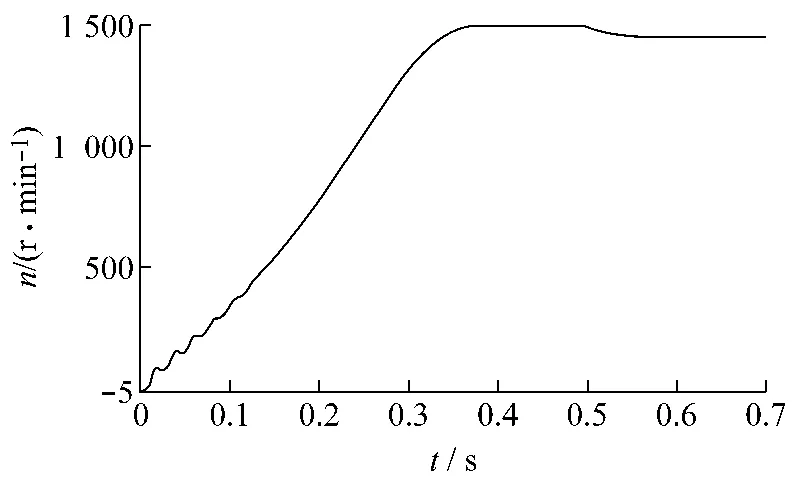
图6 电机转速波形

图7给出了定子磁链的α轴的观测值。根据三电平的模型搭载方法，采用定子磁链圆形控制策略，基于三电平供电的DTC系统能够得到接近于圆形的定子磁链输出，磁链脉动很小。

图8与图9分别给出了三电平逆变器供电的DTC系统在负载转矩5 N·m情况下稳定转速时的仿真波形，电机定子线电压峰值约为400 V，电压幅值稳定，控制周期在100 μs，定子电流峰值为5 A，电压、电流谐波分量都很小，正弦波形较好，具有良好的稳态特性。

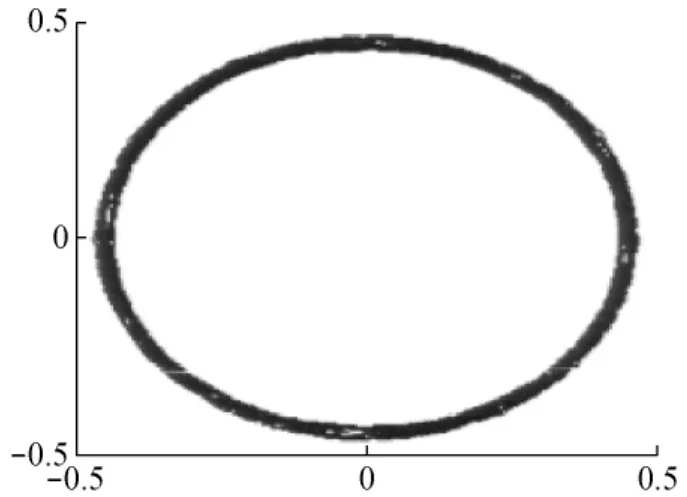
图7 定子磁链α分量

图8 电机定子相电流波形

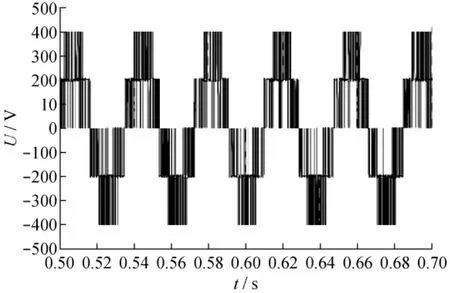
图9 电机线电压波形

5 结语

试验证明，基于三电平逆变器供电的电机DTC系统能有效抑制定子输入电流、电压的谐波分量，有效控制电机转矩、磁链脉动，提高电机转矩与转速的控制精度，系统响应时间迅速，抗干扰能力强。此外，使用三电平供电的DTC系统，降低了每个功率器件的耐压值，有效保护了电力电子器件，具有比较高的实用性。

［1］刘凤君.多电平逆变技术及其应用［M］.北京:机械工业出版社，2007.

［2］周渊深.交流调速及MATLAB仿真［M］.北京:中国电力出版社，2009.

［3］徐德鸿.现代电力电子器件原理与应用技术［M］.北京:机械工业出版社，2008.

［4］陈伯时.电力拖动自动控制系统——运动控制系统［M］.北京:机械工业出版社，2003.

［5］李永东.侯轩，谭卓辉.三电平逆变器异步电动机直接转矩控制系统(II)—合成矢量法［J］.电工技术学报，2004(5):31-35.