一类多时滞Logistic模型的周期正解

吴怀弟，阮育清

(1.福州大学数学与计算机学院，福州 350108;2.福建农林大学计算机与信息学院，福州 350002)

时滞系统是用于描述运动状态与时间历史有关的运动现象，时滞的存在给系统动力学性质的研究带来了很大的困难.对具有周期系数的Logistic时滞模型，国内外学者进行了许多相关研究［1－5］。

本文考虑如下多时滞单种群Logistic模型

其中a(t)、bi(t)、r(t)是T－周期函数;a(t)＞0，bi(t)≥0，且

根据生态学含义，考虑系统(1)的如下初值问题:

其中:τ=max{τi};φ 是［－τ，0］上的连续函数。

当m=1时，Freedman［3］运用 Horn不动点定理证明了系统(1)在函数方程 r(t)－a(t)u(t)+b(t)u(t－τ(t))=0有周期解的条件下存在周期正解。最近，对于线性多时滞的情形，Li［5］借助重合度理论获得了如下系统在条件下存在周期正解。

对于非线性的情形，文献［1－2］研究了纯时滞滞系统(4)的周期正解。

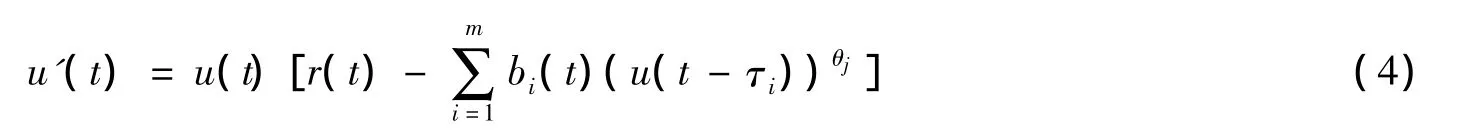
笔者借助重合度理论证得系统(4)在系统的系数都是连续正周期函数的条件下至少存在一个周期正解;注意到系统(4)和(1)是有本质差别的。系统(1)由于有正反馈时滞项，这就使得文献［1－2］的估计解的先验界的分析手法无法应用到系统(1)。由于文献［3］定理条件需要借助于解函数方程，但这并不容易做到。文献［5］所给条件仅依赖于系统的系数，非常简洁。最近Lisena［4］在研读文献［3，5］时注意到这一事实，试图获得一组介于文献［3］和文献［5］之间的条件，这一条件既要推广文献［5］的主要结果，同时又要克服文献［3］的定理条件不易验证的困难。借助Schauder不动点定理Lisena获得一组新的保证系统(1)当m=1时存在周期正解的充分性条件。如本文分析，无法将文献［1－2］的分析手法应用于系统(1)的周期正解的存在性问题，那么一个比较有趣的问题就是能否运用文献［4］的手法来探讨系统(1)周期正解存在性的条件。

1 周期正解的存在性

引理1 设k(t)＞0，a(t)＞0，bi(t)≥0，若如下的时滞函数方程

存在一个连续可微的T－周期正解，则系统(1)存在一个T－周期正解。

引理2 设a(t)、bi(t)、k(t)、r(t)是连续的T－周期函数，且

若系统

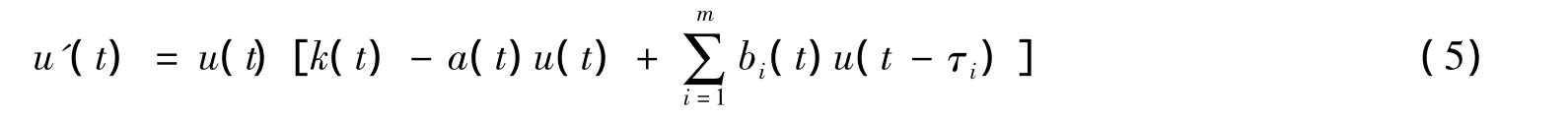
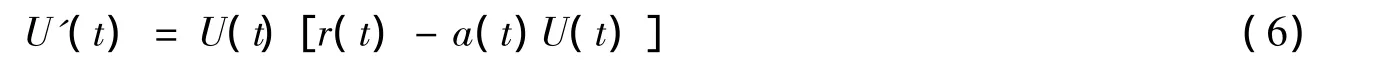
的T－周期正解，u(t)是系统(1)的一个正解，且满足

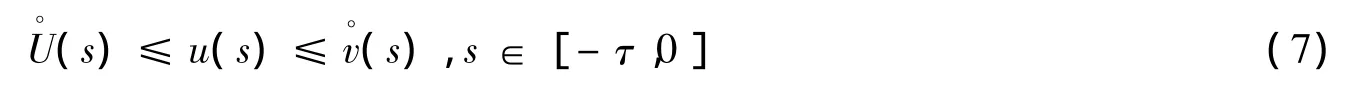
则

证明先证

故存在 t0＞0，使得又，由微分方程比较原理有又因为其为周期函数，所以式(8)成立。

由归纳法可得上述不等式在t∈［0，T］上成立。

故结论得证。

定理1 设和为引理2所定义的函数，则方程(1)存在一个T－周期正解满足

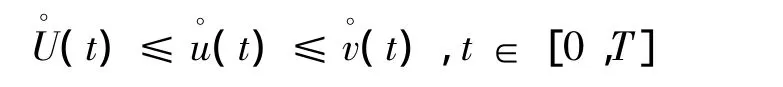
证明定义线性空间

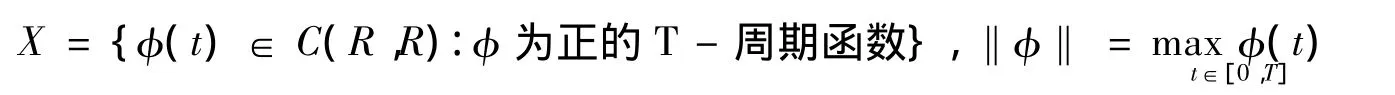
定义连续映射

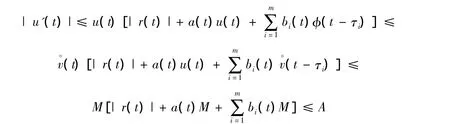
所以F(S)一致有界等度连续，因此F(S)列紧，则由 Schauder第二不动点定理得存在，使得也即方程(1)有一个 T － 周期正解满足

证明完毕。

下面给出本文主要定理的证明。

定理2 设a(t)＞0，bi(t)≥0，m［r］＞0，若存在一个正的连续可微的T－周期函数φ(t)，满足

则方程(1)有一个T－周期正解。

证明取

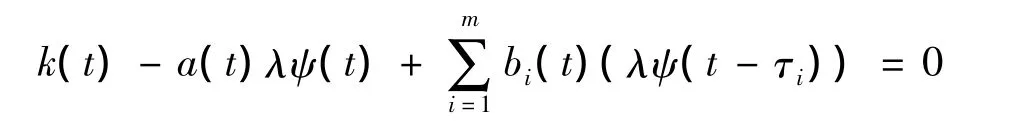
由式(9)和k(t)＞r(t)，应用定理1结论得证。

注1 文献［3］的多时滞情形要求有周期正解，这是不容易判别的，而定理2只要求存在周期函数φ(t)满足不等式，避免了函数方程的根的判别，且显然该条件也更容易满足。

注2 当取定理2中的φ(t)=1时，即为文献［5］中定理2.3所表述的内容，因此本文推广了文献［4－5］的相关工作。

［1］Chen F D，Shi J L.Periodicity in a logistic type system with several delays［J］.Computers and Mathematics with Applications，2004，48:35 －44.

［2］Chen Y M.Periodic solutions of a delayed periodic logistic equation［J］.Applied Mathematics Letters，2003，16:1047 －1051.

［3］Freedman H I，Wu J H.Periodic solutions of single-species models with periodic delay［J］.SIAM Journal on Mathematical A-nalysis，1992，23:689 －701.

［4］Lisena B.Periodic solutions of logistic equations with time delay［J］.Applied Mathematics Letters，2007，20:1070 －1074.

［5］Li Y K.Periodic solutions of periodic delay Lotka-Volterra equations and systems［J］.Journal of Mathematical Analysis Applications，2001，255:260 －280.