群发性崩塌气垫效应研究
李清山,唐红梅,陈洪凯
(重庆交通大学岩土工程研究所,重庆 400074)
群发性崩塌气垫效应研究
李清山,唐红梅,陈洪凯
(重庆交通大学岩土工程研究所,重庆 400074)
群发性崩塌具有速度大,破坏性的特点,一直以来都是按照自由落体进行研究,忽略空气的作用,这对群发性崩塌的预防和防治带来了误差。建立崩塌体垂直下落的模型,考虑空气对崩塌体的作用,通过理论推导,数值计算的方法,考虑空气外泄系数,应用空气动力学理论分析崩塌体在空气中的运动,从而得到在考虑空气效应后崩塌体到达沟谷的速度,以及封闭的空气体积。
崩塌;气垫效应;速度;空气
崩塌(Rock Avalanches),在北美国家的文献中,它“是一种非常快的顺着斜坡下方的岩石碎屑流动,在流动过程中,碎屑进一步变得破碎亦即粉碎化,其运动形式为岩石碎屑流。典型特征包括混杂大岩块的分布、运动后的表面形态和内部结构、厚度薄、分布范围大、高孔隙度、棱角状碎屑以及舌状形态”[1],地球上已知最大的第四纪岩崩位于美国加利福尼亚沙斯塔古火山地区[2]。崩塌灾害是石质山区常见的地质病害,产生源于崩塌源危岩体的形成及演变过程,属于斜坡动力地貌过程[3]。群发性崩塌破坏性更强,造成损失更加巨大,成灾范围更广的特性,因而对群发性崩塌的研究是相当重要的[4]。
国内外学者对其发生机理进行了研究,Vardoulakis(2002)基于滑体底部快速变形的剪切带与加速运动的刚性块体之间的耦合,通过提出土的摩擦速率软化与热-孔隙-力学软化的概念,以及通过修正泰勒提出的摩擦环方法,进行了热-孔隙-力学的动力学分析[5]。
Sassa(1988,2000)提出沟谷中饱水的滑坡物质由于受到来自于斜坡上方失稳的块体的快速荷载,在快速不排水条件下发生液化的启动机理[6]。Foda(1994)[7],Obayashi(1997)[8],等先后提出“底部压力波机理”[9]解释碎屑远程运动的原因。陈洪凯,等提出了危岩主控结构面损伤模型、初步建立了危岩主控结构面疲劳断裂寿命、稳定性及落石运动路径的研究等[10-13]。
对于崩滑体在空中的运动,卢万年(1991)应用空气动力学中的机翼理论分析了高速滑坡体在空气中滑行的规律,在理论上定量地分析了“空气动力擎托”的机理,提出了滑坡远程运动中滑坡速度及滑程的预测公式[14]。I.Manzella,V.Labiouse 提出用小规模的砂砾与块石流动实验来探讨崩塌的机制和特征[15]。Wieczorek,Snyder与 Waitt,等(2000)研究了美国加利福尼亚约斯曼特国家公园1996-07发生的一次不寻常的岩崩(rockfall),研究表明,岩崩从高处落下后,产生了极为明显的一股冲击气浪,冲击时岩崩具有的相对高速度为110~120 m/s[16]。陈洪凯,等[17]认为崩塌体下落过程中,在底部封闭了一定体积的压缩空气,在碎屑流运动过程中对其起到气垫效应,崩塌体在沟谷运动期间,底部应该存在一定厚度的空气压缩层,碎屑流的气垫效应显著。拜格诺德和美籍华人许靖华先后提出高速滑坡运动的“无黏性颗粒流说”;Kent提出“圈闭空气导致流体化说”;Shreve提出“气垫层说”;Habib,等提出“孔隙气压力说”;Erisman提出“岩石自我润滑说”。这些观点是20世纪80年代以前提出的关于高速崩滑启程与远程运动的主要机理[18-19]。孙萍,等[20]提出了“圈闭气垫效应飞行阶段”,但是没有进行详细的计算。
1 建立模型
笔者考虑到崩塌体下落过程中空气对其作用,认为崩塌体垂直下落,崩塌体体积、质量已知。由于崩塌体在下落过程中压缩其下部空气,所以压缩空气会给崩塌体一个上举力。崩塌体下落过程中,会推动其下部与其相邻的最近一层空气同时向下运动。崩塌体下部距离地面的高度一定,空气在向下运动的过程中,由于地面的沟谷地貌,以及四周没有封闭,所以部分空气会被压缩,而部分空气会沿四周流出,即偏向崩塌体外面流动,如图1。由于沟谷地貌利于封闭空气形成压缩空气,随着崩塌体的下落,上举力越来越大。将崩塌体近似视为具有一定体积和厚度的多孔介质板,其下部沟谷的横剖面形状为弧形,开口向上,半径为r,深度为h,认为崩塌体为垂直下落。在上举力的作用下,崩塌体的下落加速度减小,但速度在增大,所以崩塌体做加速度在减小的加速运动。为了对其进行研究,将崩塌体在空气中的运动近似等效为活塞在充满空气的管中运动,初始时刻,管中空气为静止状态,压强、密度、温度与大气压强、密度、温度相等。活塞质量与崩塌体质量相等,初始速度等于崩塌体初始速度v0。
由于崩塌体在下落过程中有空气的逸出,所以在对崩塌体下部空气进行研究时利用积分很难进行计算,这里对其运用数值计算,进行分段推导,利用VB语言编程进行计算。
崩塌体距离地面H,将其n等份,每等份长度为dh=H/n,取c足够大,dh就足够小,则密度、压强、加速度在dh上的变化就为一微量。其运动过程如图2。

假设崩塌体从t=0开始加速运动,如图2(a),经极短时间t1后,运动距离dh,产生1道微弱的压缩波,崩塌体速度从v0增加到v1,崩塌体下部空气先受到压缩,其压强、密度、温度略有提高,同时产生1道微弱的压缩波A1—A1在管内以声速c0推进。凡是此波扫过之处,空气的压强由波前P0升高到P1、密度由 ρ0升高到 ρ1、温度由 T0升高到 T1,速度也升到v1。压缩波A1—A1下部的空气仍然处于初始状态如图2(b)。
当崩塌体运动dh距离后,继续向下运动,于是A1—A1波后空气又受到压缩,在A1—A1波后的气体产生1道新的压缩波A2—A2,它的绝对传播速度为c0+△v,c1为空气在第2道压缩波中的传播速度,由于该波在第1道压缩波后的空气中传播,因此c1>c0,可见第2道波的传播速度必大于第1道波的传播速度,凡是此波扫过之处,空气的压强由波前P1升高到P2、密度由ρ1升高到ρ2、温度由T1升高到T2,速度也升到v2如图2(c)。
当崩塌体运动2 dh距离时,继续向下运动,在A2—A2波下部的空气中产生新的压缩波A3—A3,它的绝对传播速度为c2+△v,c2为空气在第3道压缩波中的传播速度,由于该波在第2道压缩波后的空气中传播,因此c2>c1,可见第3道波的传播速度必大于第2道波的传播速度,凡是此波扫过之处,空气的压强由波前P2升高到P3、密度由ρ2升高到ρ3、温度由T2升高到T3,速度也升到v3如图2(d)。
依此类推,当时间由t=0开始,经过一段有限的时间间隔达到tk时,在崩塌体下部应有无限多道微弱的压缩波,形成一个连续的区域A—B。因此A—B区内不是有限的少数几道波(呈台阶形),而是无数道波,所以压强分布就不是台阶形,而是一条连续曲线如图2(e)。
在这里还要考虑后面产生的压缩波会不会越过第1道压缩波形成新的压缩区。因为后波之所以能追上前波的原因是,当后波扫过空气时,这块空气已被前波扫过,压强和稳定都增大了,所以,后波的传播速度就增大了。如果,各道波都集中在一起了,后波追上前波的条件不具备了,所以,最后结果只能是所有的波全叠在一起,以某个共同的速度推进,而不可能有某一道子波超前[21]。由于是崩塌体推着空气运动,所以,空气运动速度等于崩塌体运动速度。
2 空气效应时崩塌体下落的公式推导
由于崩塌体在下落过程中是连续的,每一段dh的运动都是连续的,后一段dh依赖于上一段dh,所以从中取出崩塌体在第 i(i∈(1,2,···,n))段 dh运动进行研究(图3),并推导出以下公式:


图3 压缩波公式推导示意Fig.3 Deduction schemes of compression wave formula

压缩波的前进长度为:
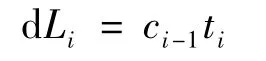
压缩后,即2—2截面与3—3截面之间的体积为:
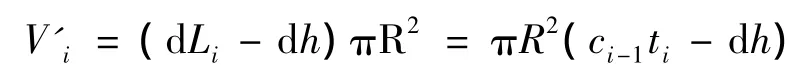
由于压缩过程中有部分空气逸出控制体,所以压缩前后质量m发生了变化。
式中:ai为崩塌体在第i段dh运动期间的加速度;Pi-1为崩塌在运动完第i-1段dh时压缩空气给崩塌体的压强;vi-1为崩塌在运动完第i-1段dh时崩塌体的速度;ti为崩塌体在第i段dh运动所需要的时间;ci-1为崩塌体在第i段dh运动期间产生的压缩波在前一段(第i-1段dh)运动产生的压缩空气中的传播速度;ρi-1为崩塌在运动完第i-1段dh时压缩空气的密度;dLi为崩塌体在第i段dh运动期间产生的压缩波前进的长度。
则,压缩后密度为:

X为在压缩过程中由1-1截面与3-3截面之间逸出的气体,由于压缩后气体密度必增大,所以可以将X写成X=αidh形式,其中,αi表示空气外泄系数0< αi<1。

崩塌体运动完第i段dh压强后其下部压缩空气压强为:

崩塌体速度为:vi=vi-1+aiti
由于崩塌体距离地面的高度是一定的,所以压缩波最后会跟地面接触,假设压缩波不被地面反射,全部被地面吸收。即:
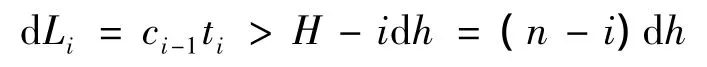
表示在崩塌体运动dh长度时压缩波也传播到了地面,则此后压强不是在以曲线运动,而是出现突变,如图2(f)。则各参数变化为:

此时,压缩前气体体积为:
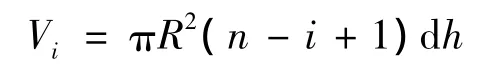
压缩后气体体积为:

压缩前质量为mi:

压缩后质量为m':

压缩后密度为:

崩塌体运动完第i段dh压强后其下部压缩空气压强为:

由于下落过程中,崩塌体速度逐渐增多,气体压强也逐渐增大,而如果崩塌体的重力与下部压缩空气给崩塌体的上举力相等时,达到极限状态,此后,崩塌体将以匀速下落。即:
如果当i=m时
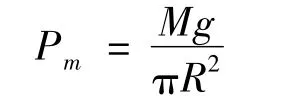
则,当 i>m时
加速度:ai=0
压缩空气密度为:

崩塌体运动速度为:vi=vm
崩塌体落地时的速度即为vi,压缩以后空气的密度远远大于开始时空气的初始密度,在空气被压缩的过程中最重要的是如何确定系数αi,其直接影响压缩过程中密度和压强的变化。由于下落时间较短,以及为了计算的简单,先假设崩塌体下落过程中温度,声速均为初始温度和声速,取αi为定值。综合考虑,每一段dh长度可根据情况取1 m或2 m左右。
当崩塌体落到地面时,由于沟谷状地貌,在崩塌体下部封闭的空气体积计算图4。

图4 封闭气体体积计算Fig.4 Calculation schemes of closed gas volume

3 算例
2009年6 月5 日,重庆市武隆县铁矿乡鸡尾山发生山体崩滑特大地质灾害,此次灾害导致坡脚一煤矿和铁矿乡6户居民家淹没,80余人被埋遇难。鸡尾山山脉呈N55°E向展布,总体地形为北东高南西低,呈单面山斜坡,地形坡角一般20~40°,陡崖发育,陡崖高度50~150 m。最高点标高1 442 m,最低点铁匠沟标高1 000 m,相对高差442 m。属中山地貌。已崩滑区长约700 m左右,后壁高度90~100 m,宽度110 ~120 m,平均厚约60 m,面积约8.4万m2,体积约500万m3;加之崩滑过程中冲垮的山体近300万m3,崩滑体总体积约800万m3。崩滑体为灰岩,沿下伏软弱岩层层面滑动,滑动方向约345o。崩滑堆积体长约2 170 m,最大宽度470 m,面积约46.8万m2。崩塌体运动区域的纵剖面图如图5,3—3为经过崩塌区的横剖面图如图6,由资料和纵横剖面图分析可得,崩塌体跃下前缘约100 m高的陡坎后解体,在底部气垫效应的作用下高速运动,碎屑流堆积长度达2 170 m左右。

图5 碎屑流纵剖面Fig.5 Longitudinal plan of debris flow

图6 3-3横剖面Fig.6 3 -3 Transverse section
由表1可知,对于不同的外泄系数,崩塌体的速度也不同,随着外泄系数的增大,崩塌体速度也在增大,当α=1时,其速度最大,也就是自由落体速度,而随着外泄系数的增大,压缩空气对上部崩塌体的上举力在减小,当α=1时,上举力为0,也就是忽略了下部压缩空气的作用,当α=0.2时,崩塌体速度为34.37 m/s,当 α =1时(自由落体),崩塌体速度为44.29 m/s,两者相差10 m/s,由此可知,压缩空气在崩塌体下落过程起着重要作用,是不能忽略的,它对研究崩塌体的运动具有重要意义。
由图7,空气外泄系数与崩塌体速度关系曲线可以得出,崩塌体速度与外泄系数是按一定的规律变化的,总体来看,崩塌体速度是随着外泄系数的增大而增大的,但是当α=0.2~0.6时,崩塌体速度随着外泄系数的增大增长比较快,说明在这个阶段压缩空气对崩塌体的作用比较明显,当α=0.6~0.8时,崩塌体速度随着外泄系数的增大增长比较平缓,当α=0.8~1时,曲线近似水平,说明在此阶段,由于空气基本全部外泄,崩塌体受压缩空气的作用已经变小,近似自由落体,α=0.6是一个过渡点。由此可见压缩空气对崩塌体速度的影响是一个不可忽略的因素。

图7 空气外泄系数与崩塌体速度关系曲线Fig.7 Related curve between the air leakage coefficient and the speed of landslip

表1 崩塌体速度Tab.1 Collapsing velocity
4 结论
笔者主要研究了在群发性崩塌体下落过程中,下部空气对其影响,进行了理想假设,建立了考虑空气效应的群发性崩塌垂直下落的模型,并进行了理论推导,通过对实例计算,得到了不同外泄系数时,崩塌体落到沟谷时的速度。由图表可知,崩塌体下落过程中,其下部压缩空气对其起着不可忽略的作用,尤其是当沟谷比较深,有利于空气的封闭时,此时的空气效应更加显著,所以在以前的研究中将崩塌体的下落视为自由落体是不合理的。当外泄系数为1时,即为自由落体,由公式计算得到的崩塌体速度与按自由落体计算得到的速度值基本相等,说明本文的假设以及理论推导的准确性。
(References):
[1] Jackson J A.Glossary of Geology(Fourth Edition)[M].Virginia:American Geological Institute,1997:556-557.
[2] Crandell D R.Miller C D,Glicken H X.Catastrophic debris avalanche on ancestral Mount Shasta volcano,California[J].Geology,1984,12:143-146.
[3] 陈洪凯,鲜学福,唐红梅.石质山区崩塌灾害形成机制——以四面山国家级风景名胜区红岩石为例[J].西川大学学报,2010,42(3):1-6.
CHEN Hong-kai,XIAN Xue-fu,TANG Hong-mei.Developing mechanism for collapse disaster in rocky mountain area-taking Mt.Hongy-an in the national scenic spots of simianschan as an example[J].Journal of Sichuan University,2010,42(3):1-6.
[4] 王林峰,陈洪凯.危岩链式规律的力学演绎[J].重庆建筑大学学报,2008,30(2):94-97.
WANG Lin-feng,CHEN Hong-kai.Mechanical illation for chained regularity of perilous rock[J].Journal of Chongqing Jianzhu University,2008,30(2):94-97.
[5] Vardoulakis I.Dynamic thermo-poro-mechanical analysis of catastrophic landslides[J].Geotechnique,2002,52(3):157-171.
[6] 程谦恭,张卓元,黄润秋.高速远程崩滑动力学的研究现状及发展趋势[J].山地学报,2007,22(1):72-84.
CHENG Qian-gong,ZHANG Zhuo-yuan,HUANG Rui-qiu.Study on dynamics of rock avalanches:state of the art report[J].Journal of Mountain Science,2007,22(1):72-84.
[7] Foda M A.Landslides riding on basal pressure waves[J].Continuum Mechanics and thermodynamics,1994,6:61-79.
[8] Kobayashi Y.Long runout landslides riding on a basal guided wave[C]//Engineering Geology and the Environment.Rotterdam:A.A.Balkema,1997:761-766.
[9] Zhang D,Foda M A.An in stability mechanism for the sliding motion of finite depth of bulk granular materials[J].Acta Mechanica,1997,121:1-19.
[10] Chen H K,Tang H M ,Ye S Q.Damage model of control fissure in perilous rock[J].Applied Mathematics and Mechanics:English Edition,2006 ,27(7):967-974.
[11] Chen H K,Tang H M.Method to calculation fatigue fracture life of control fissure[J].Applied Mathematics and Mechanics:English Edition,2007,28(5):643-649
[12]陈洪凯,唐红梅,王蓉.三峡库区危岩稳定性计算方法及应用[J].岩石力学与工程学报,2004 ,23(4):614-619.
CHEN Hong-kai,TANG Hong-mei,WANG Rong.Calculation method of stability for unstable rock and application to the three gorges reservoir[J].Chinese Journal of Rock Mechanics and Engineering,2004 ,23(4):614-619.
[13]唐红梅,易朋莹.危岩落石运动路径研究[J].重庆建筑大学学报,2003 ,25(1):17-23.
TANG Hong-mei,YI Peng-ying.Research on dangerous rock movement route[J].Journal of Chongqing Jianzhu University,2003 ,25(1):17-23.
[14]刑爱国,殷跃平.云南头寨滑坡全程流体动力学机理分析[J].同济大学学报,2009,37(4):481-485.
XING Ai-guo,YIN Yue-ping.Whole course analysis on Hydrokinetics mechanism of Touzhai gully landslide[J].Journal of Tongji University,2009,37(4):481-485.
[15] Manzella I,Labiouse V.Flow experiments with gravel and blocks at small scale to investigate parameters and mechanisms involved in rock avalanches[J].Engineering Geology,2009,109(1-2):146-158.
[16] Wieczorek G L,Snyder J B,Waitt R B.Unusual july 10,1996,
rockfall at happy isles,yosemite national park,california[J].Geological Society of America Bulletin,2000,112(1):75-85
[17]陈洪凯,唐红梅,王林峰,等.危岩崩塌演化理论及应用[M].北京:科技出版社,2009:231-237.
[18]胡广韬.滑坡动力学[M].北京:地质出版社,1995:16-22.
[19]程谦恭,彭建兵,胡广韬,等.高速岩质滑坡动力学[M].成都:西南交通大学出版社,1999:1-7.
[20]孙萍,张永双,殷跃平,等.东河口滑坡-碎屑流高速远程运移机制探讨[J].工程地质学报,2009,17(6):737-744.
SUN Ping,ZHANG Yong-shuang,YIN Yue-ping,et al.Discussion on long run-out sliding mechanism of donghekou landslide-debri s flow[J].Journal of Engineering Geoloty,2009,17(6):737-744.
[21]钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2004.
On Air Cushion Effect of the Mass Avalanches
LI Qing-shan,TANG Hong-mei,CHEN Hong-kai
(Institute of Geotechnical Engineering,Chongqing Jiaotong University,Chongqing 400074,China)
The mass landslip takes rapidity and destructive characteristics.Without taking the function of air into accout,studied by free fall for a long time,it could lead to errors for the prevention and control of the landslip.The model of vertical drop collapse body was established;a more accurate quantitative analysis method for analyzing the practical issue and estimating disasters was obtained,which was proposed by considering the speed of collapse body reached gully after the air affect and closed air volume.By considering the role of air to collapse body,the air out releasing coefficient was calculated through the theory derivation and numerical calculation method.
landslip;air cushion effect;speed;air
P642.21,O355
A
1674-0696(2011)05-0983-00
10.3969/j.issn.1674-0696.2011.05.021
2011-05-10;
2011-06-10
国家自然科学基金资助项目(50678182)
李清山(1985-),男,甘肃景泰人,硕士研究生,主要从事危岩崩塌运动研究。E-mail:lqs20052748@163.com。

