悬索桥锚跨索股分析及程序实现

肖 军，张永水，董 义

（重庆交通大学土木建筑学院，重庆 400074）

悬索桥锚跨索股分析及程序实现

肖 军，张永水，董 义

（重庆交通大学土木建筑学院，重庆 400074）

针对悬索桥锚跨索股的特点，介绍了索股几何长度迭代计算原理、索力计算模式、索股稳定性判据，并据此编制了FORTRAN数值计算程序，克服了以往悬索桥锚跨索股设计时曾采用的虚交点法导致计算索股与锚面的交点同设计有较大差异的问题;以某在建大型悬索桥为实例进行了锚跨索股分析，得出了相应结论。

锚跨索股;几何长度;无应力长度;索力模式;稳定性判据

近年来，我国相继修建了虎门大桥、江阴长江大桥等大跨悬索桥，对于中边跨主缆，利用有限位移理论或者基于悬链线的无应力状态法，能够精确地计算主缆的无应力长度等参数，对于锚跨部分则一直是一个难点。以往在设计的时候，采用虚交点法，导致设计和计算的锚固点坐标有较大差异，悬索桥锚跨索股在悬索桥整个结构中只占很小一部分，但其关系到散索鞍和锚固系统设计的合理性和主缆索股下料长度计算的精度。笔者主要介绍悬索桥锚跨索股分析的主要原理，包括各索股几何长度迭代计算及索力计算模式，索股稳定性判据，根据相应的分析原理编制了FORTRAN计算程序，并对在建中的某大型悬索桥锚跨索股进行了实例分析，得到一些结论。

1 散索鞍构造及锚跨索股特点

1.1 散索鞍构造特点

散索鞍布置在边跨和锚跨之间的支撑平台上，其主要作用是为主缆提供支承，将主缆的竖向压力均匀地传递到支墩上;同时使得主缆索股经过散索鞍后能够平顺的改变方向，在竖直方向和在水平方向散开，将各索股引入锚面的对应锚固点位置。散索鞍构造形式分滚轴式和摇轴式2种，摇轴式散索鞍鞍体底部是一个长条形凹槽，内嵌摆轴的上下承板，支撑在安装底座的弧面钢轴上，缆力变化时，鞍头纵向摆动，使整个索鞍在弧面钢轴上作相应摆动。图1为摇轴式散索鞍立面和平面构造。

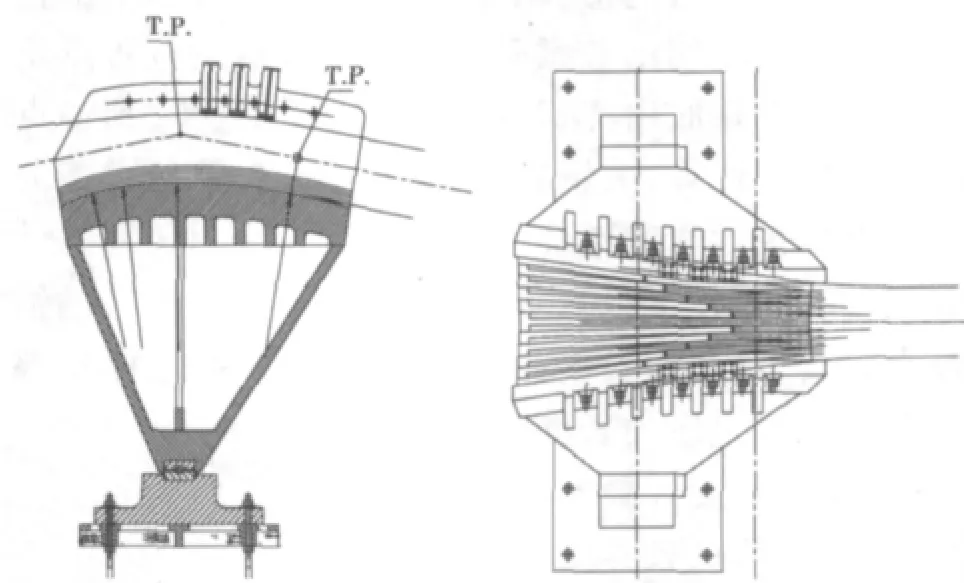
图1 散索鞍立面和平面构造Fig.1 Map of saddles’flat and fac ade structure

1.2 锚跨索股特点

组成主缆的索股都是按确定的位置排列的，无论在塔顶主鞍处、散索鞍处和在锚锭中的锚固架处，每根索股都有它自己的确定位置［1］，如图2。

图2 索股断面布置Fig.2 Diagram of strand cross-section layout

就整个主缆在散索鞍处的形状而言，具有以下特点:

1）在竖向平面内，应保证主缆的最外层索股经过散索鞍后，仍有一个向下的转角，即δ-ζ-θ＞0，其中:δ为主缆出散索鞍的转角;ζ为主缆入散索鞍的切线角;θ为散索角。而δ、ζ和θ等角度与整个悬索桥的总体布置有关，也与锚面布置以及散索长度有关。

2）在水平面内，由于锚固的需要，索股必须在锚面上散开来。散开的范围大小与锚面的尺寸大小和散索的长度有关。

3）主缆在散索鞍处，各个索股既有竖向弯曲，又有平面弯曲。各索股平弯半径大于竖弯半径，同时，为了保持有垂直压力及一定的摩擦力，索股的竖弯弧线长度必须大于平弯弧线长度。

2 锚跨索股计算原理

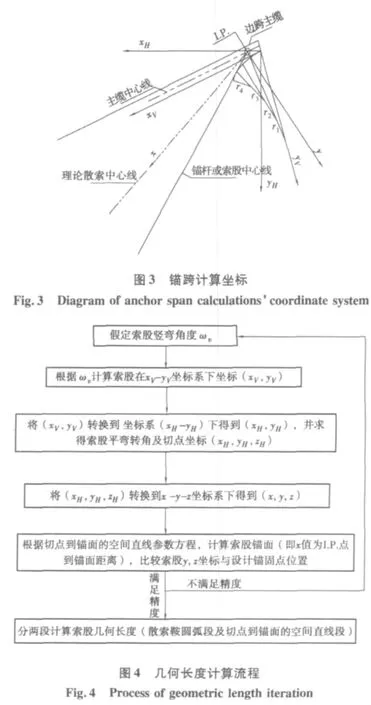
索股绕过散索鞍的部分，必然是在散索鞍的槽路的约束下平滑的散开，至于索股具体从哪个部位以多大的角度切出散索鞍与锚面上锚点的位置息息相关。对于索股由T.P.点（索股平弯起点）到锚点的索股长度计算，关键在散索鞍上的索股与索鞍的切点以及转索角的精确计算。索股无应力长度的计算，需在几何长度计算基础上，求得与实际相符的锚跨索股索力，几何长度扣除索股因索力弹性伸长部分即为索股无应力长度。

2.1 几何长度计算方法

2.1.1 全局迭代算法

本法从索股在散索鞍中的稳定排列（如图2）出发，根据锚固点设计的相对位置及散索鞍与锚面的相对位置，在散索鞍分段空间圆弧全局内迭代计算出索股在散索鞍处的竖弯转角、平弯转角，使得这些参数在初始选择时就更合理和恰当［2］。鉴于索股与散索鞍的切点坐标与索股的竖弯角度和平弯角度直接相关，首先假设索股的竖弯角度，计算索股在假定竖弯角度下在xV-yV坐标系（坐标系参见图3）下切点坐标（xV，yV），然后将切点坐标换算到xH-yH坐标系下得到（xH，yH），并在xH-yH-zH坐标系下，求得索股平弯转角及切点坐标（xH，yH，zH），最后将切点（xH，yH，zH）转化到x-y-z坐标系下，并按照 tan φ2=tan ωp× cos α （其中，φ2是索股在x-y-z坐标系中与x轴夹角，ωp是索股的平弯转角，α是索股与散索中心线夹角）修正索股在xz平面上与x轴夹角后，用参数方程表示索股在切点和锚点之间的空间直线，按此参数方程在x-y-z坐标系下，计算到锚面，比较计算坐标与设计锚点坐标，满足精度则认为索股形状正确;若不满足，则修正竖弯角度重新进行迭代计算，直到锚点计算坐标和设计坐标满足精度为止。计算流程见图4。

2.1.2 局部线性迭代法

本算法在计算索股竖弯角度时，首先判断出各索股切点位置所在区间，然后进行线性迭代计算出各索股竖弯转角，结合平弯角度，进而推算出索股锚固点空间坐标［3］。图5为锚跨索股竖弯角度计算简图。

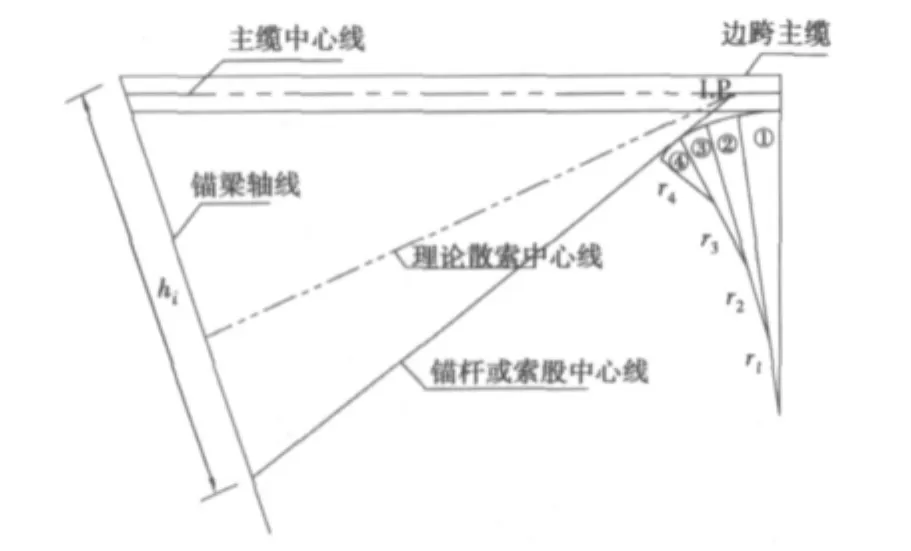
图5 竖弯角度计算Fig.5 Diagram of vertical bending angle calculation

竖弯角度具体计算步骤如下:

1）已知参数。散索鞍内各索股的具体位置，如图2所示;索槽的4种竖弯曲线半径为r1～r4;锚跨跨径及理论中心线转角;锚杆锚梁连接点之间的距离，即已知图5中的hi值（i指待求索股号）。

2）将索槽按曲线半径大小分为4个区间（半径相同为一个区间），分别计算各区间交汇点处的hi1、hi2、hi3。

3）判定该索股脱离索槽（切点）的区间有:即:hi＜hi1时，切点在①区;hi1≤hi≤hi2时，切点在②区;hi2≥hi≤hi3时，切点在③区;hi＞hi3时，切点在④区。

4）切点区间确定以后，建立该区间索股线性几何方程，迭代计算出索股中心线（锚杆中心线）与锚梁夹角。

结合索股平弯计算结果（平弯计算较简单，本文略），可以计算出索股的锚固点坐标，同时精确计算出索股力的大小，可以求得索股无应力长度，空缆到成桥的锚跨索力增量引起的中心索股弹性伸长量除以摇轴半径可以得到散索鞍预偏角。

2.2 锚跨索股索力计算模式［4－6］

锚跨索股分析时，通常有以下平衡条件需要考虑:①索股相对于索鞍不滑动;②散索鞍的平衡条件;③散索鞍支墩的平衡条件。鉴于散索鞍支墩抗剪抗弯刚度都很大，条件③一般不予单独考虑。考虑条件①时，边跨和锚跨索股在不计入摩擦情况下，索力合力值相等［7］。考虑条件②时，针对滚轴式散索鞍，即是边锚跨索股合力沿滑面分力相等，对于摇轴式散索鞍而言，则需要边跨和锚跨索股相对于散索鞍摇轴中心力矩平衡。笔者针对摇轴式散索鞍，介绍2种索力分配模式。

模式1:索力均等且近似等于边跨各索股索力值以满足索股相对索槽不滑动条件。基于理想情况下，索力均匀，各索股安全系数相等，可提高悬索桥整体安全系数。

模式2:索力取与索股距摇轴中心转动半径成正比分配模式，即Ti/T0=Ri/R0（其中，Ti、T0分别为编号为i的索股索力及中心索股索力;Ri、R0分别为编号为i的索股距摇轴中心转动半径及中心索股距摇轴中心转动半径）。主要考虑，在预偏角度较小的情况下，空缆到成桥过程中，散索鞍绕摇轴中心转动，使得远离摇轴中心的索股，弹性伸长量更大。

结合整体条件及索股索力分配模式，可以方便的计算出各索股索力值，几何长度扣除索股因索力弹性伸长部分即为索股无应力长度。

2.3 索股稳定性判据

为使主缆索股按照一定的排列次序分散到预定的锚固点上，索股在通过散索鞍时必须有水平和竖向2种变形。索股在索鞍中沿水平圆弧曲线散开的同时，必须在竖直方向上保持一定的压力，使索股本身始终压在下层索股（或索槽）上，否则索股就会处于不稳定状态，形成堆积，导致索股钢丝排列无序、索股的实际长度和理论长度不符、索鞍构件受损等严重后果，以致无法顺利施工。小西一郎编著的《钢桥》［8］一书指出:为使各索股钢丝在散索鞍中的配列保持稳定，必须保证:

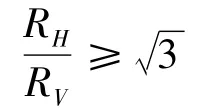
式中:RH为索股平弯半径;RV为索股竖弯半径。

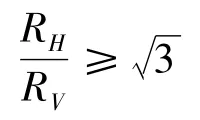
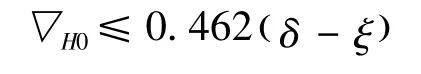
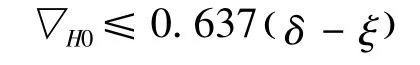
综合以上分析，锚跨索股稳定性判据如下:

1）当▽H0＜ 0.462 （δ-ξ）时，索股是完全稳定的。

2）当 0.462 （ δ -ξ） ＜▽H0＜ 0.637 （ δ -ξ）时，索股是基本稳定的，前提是钢丝索股之间存在有摩擦力。

3）当▽H0＞ 0.637 （δ-ξ）时，索股是不稳定的。

索股稳定性判据，能够方便的加入锚跨索股分析程序中对索股稳定性加以判定。

3 实例计算

某在建大型悬索桥，由南向北跨径组成为:18.867 m（南锚跨）+245 m（南边跨）+788 m（中跨）+245 m（北边跨）+17.831 m（北边跨）。本实例采用全局迭代方法，依据编制的悬索桥锚跨索股分析程序［10］进行了该桥南锚跨索股分析，其中，边跨主缆索力由悬索桥上部结构分析专用程序SBCC3.0计算得到，该桥南锚跨索股部分分析结果见表1。

表1 某悬索桥锚跨索股分析结果Tab.1 Analysis of suspension bridge anchor span strand

索股几何长度可根据Autocad软件作图查询得到，表1中各索股几何长度均经过作图验证。另外，由表1可以得出以下比较结果:

1）2 种索力计算模式计算所得索股无应力长度差异在2 cm以内。

2）索力模式2较模式1计算所得各索股索力值差异在10%以内。

通过以上分析，为了有效提高悬索桥主缆的安全系数，需要在悬索桥施工过程中或者在成桥后对锚跨索股进行张拉控制，使得各索股索力均匀。

4 结语

笔者主要介绍了悬索桥锚跨索股分析的计算原理，根据悬索桥锚跨索股特点编制的悬索桥锚跨索股计算程序，能够准确的计算各索股几何长度、无应力长度及索力值。另外，鉴于锚跨在锚面和索股之间设有锚固拉杆，一般留有至少几十厘米的可调节空间，并且锚跨索股主要以索力控制，而不是线形，因此，对于2种索力模式计算的无应力长度和索力，建议索力模式1供主缆下料长度计算使用及作为成桥后索力调整目标，索力模式1供施工过程中索力监控使用。

（References）:

［1］ 周孟波.悬索桥手册［M］.北京:人民交通出版社，2003.

［2］ 罗喜恒，林长川.悬索桥锚跨索股分析［C］//江阴长江公路大桥工程建设论文集.北京:人民交通出版社，2002.

［3］ 牛和恩.虎门大桥工程:第2册［M］.北京:人民交通出版社，1998.

［4］ 沈锐利，薛光雄.悬索桥主缆丝股锚固力的计算方法探讨［J］.桥梁建设，2003（6）:25-29.

SHEN Rui-li，XUE Guang-xiong.Study of calculation methods for anchorage force of main cable wire strands of suspension bridge［J］.Bridge Construction，2003（6）:25-29.

［5］ 罗喜恒，肖汝诚，项海帆.悬索桥锚跨索股分析研究［J］.公路交通科技，2004，21（12）:45-53.

LUO Xi-heng，XIAO Ru-cheng，XIANG Hai-fan.Analysis study of anchor span strand for suspension bridge［J］.Journd of Highway and Transportation Research and Development，2004，21（12）:45-53.

［6］ 唐茂林，沈锐利，强士中.大跨度悬索桥丝股架设线形计算的精确方法［J］.西南交通大学学报，2001，36（3）:303-307.

TANG Mao-lin，SHEN Rui-li，QIANG Shi-zhong.An accurate calculation method for ercting curves of wier strands of long suspention bridges［J］.Journal of Southweast Jiaotong Univesity，2001，36（3）:303-307.

［7］ 林恰，崔冰，唐茂林，等.边跨主缆角度对悬索桥的影响分析［J］.重庆交通大学学报:自然科学版，2010，29（3）:336-339.

LIN Qia，CUI Bing，TANG Mao-Lin，et al.Influence analysis on main cable angle of side span of suspension bridge［J］.Journal of Chongqing Jiaotong University:Natural Science，2010，29（3）:336-339.

［8］ ［日］小西一郎.钢桥［M］.朱立冬，译.北京:人民铁道出版社，1984.

［9］ 张克，段玉凤.悬索桥主缆索股在散索过程中的稳定［C］//江阴长江公路大桥工程建设论文集.北京:人民交通出版社，2002.

［10］ 谭浩强，田淑清.Fortran语言——Fortran 77结构化程序设计［M］.北京:清华大学出版社，1998.

Suspension Anchor Span Strand Analysis and Program Implementation

XIAO Jun，ZHANG Yong-shui，DONG Yi
（School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China）

According to the characteristics of suspension bridge anchor span strand，the iterative calculation theory of the geometric length，cable force calculation model and the stability criterion of span strand were introduced;based on FORTRAN numerical calculation procedure，the significant difference between the designs of calculation cable strand and anchor intersection due to previous application of virtual intersection method when designing suspension bridge anchor span strand was overcome;based on a large suspension bridge under construction，a conclusion had been drawn.

anchor span strand;geometric length;unstressed length;cable force model;stability criterion

U442.53

A

1674-0696（2011）05-0907-04

10.3969/j.issn.1674-0696.2011.05.005

2011-05-16;

2011-06-18

肖 军（1987-），男，四川邻水人，硕士研究生，主要从事大跨径桥梁设计理论方面的研究。E-mail:sunflower001@foxmail.com。