基于EI及MAC 算法的连续刚构桥传感器优化布置
何 华,张力文,周建庭,杨建喜,周 磊
(1.广西吉泰投资有限公司,广西南宁 530001;2.重庆交通大学土木建筑学院,重庆 400074)
基于EI及MAC 算法的连续刚构桥传感器优化布置
何 华1,张力文2,周建庭2,杨建喜2,周 磊2
(1.广西吉泰投资有限公司,广西南宁 530001;2.重庆交通大学土木建筑学院,重庆 400074)
介绍了有效独立法(EI)和模态保证准则(MAC)的工作性能与适用范围,并结合各自优点,得到了一种新型的混合算法。将此方法运用到以龙河大桥为研究对象的连续刚构桥传感器布置上。结果表明:基于EI及MAC混合算法得到的测点截面位置有别于人为凭借经验将传感器布置在根部、边跨及中跨1/4倍数截面等位置;通过MAC值验算,连续刚构桥传感器布置在此方法下能得到满意的优化结果。
有效独立法;MAC法;连续刚构桥;传感器优化布置
近年来,我国对桥梁的传感器优化布置领域的研究已趋成熟,有大量的算法涌现在各类桥梁的传感器优化布置过程当中,为解决实际的优化问题提供了理论依据。笔者研究的连续刚构桥的传感器优化布置,选择一种针对性强且有效的数学算法至关重要。
目前研究热点是一种模仿生物自然进化过程的随机优化算法——遗传算法。基于遗传算法的基本原理衍生出了一种基于EI及 MAC的混合算法[1-2]。EI这种方法经常用于解决优化问题,是通过从原始数据群(测点群)里剔除测点的过程。其实质是依次删除对复合模态E矩阵的秩贡献最小的自由度,从而来优化Fisher信息矩阵[3],整个思路结合了E矩阵的幂等性,在最少测点的前提下,使感兴趣的模态向量尽可能保持线性无关。基于列主元QR分解技术[4]的MAC法是向初始测点群中添加测点的过程。这种方法首先是将模态矩阵进行列主元QR分解,这样就能够保证得到使模态向量保持较大空间交角对应的初始测点,接着向这组测点群里添加测点,当添加的测点可以让MAC矩阵中非对角元素达到最小时,这个测点将被收集到初始测点群中,并扩充成为下一个初始测点群,重复此过程,直至达到满意的测点数。最终得到的测点能够保证所测得的向量具有最大的空间交角。整个过程将模态保证准则作为测点布设方案的评价标准。结合了这2种方法的混合算法可以解决桥梁传感器布置问题,并最终达到优化,二者的关系如图1。这种混合算法利用其各自的优点,可以避免添加测点的经验性,并且能够保证添加测点后,测得向量的正交性和线性无关性。
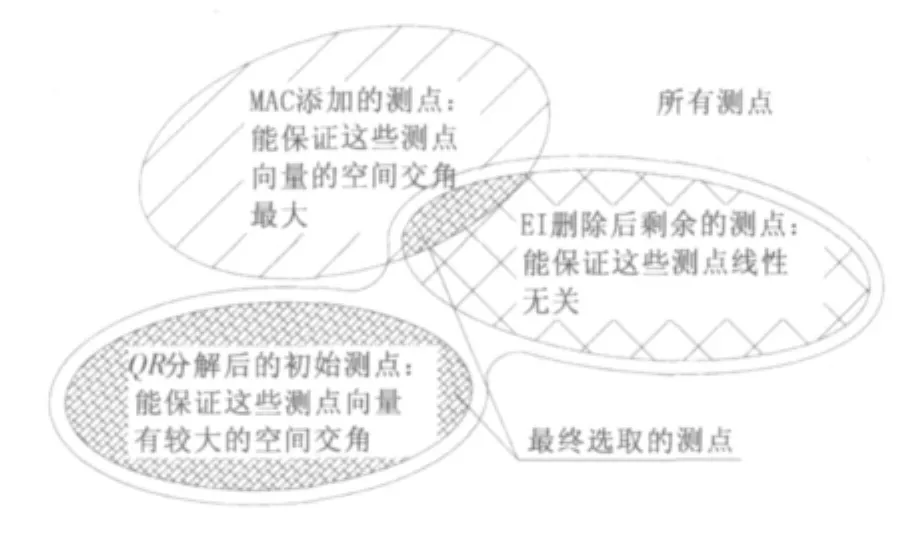
图1 算法关系Fig.1 Relationship between mathematical methods
1 算法理论
1.1 动力特性分析[5-6]
求解非阻尼自由振动条件下的振型和固有周期的特征方程式如式(1):

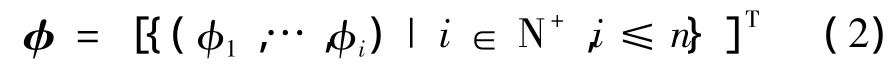
1.2 混合算法
1.2.1 列主元QR分解法
基于列主元的QR分解法利用了测量向量的行空间特性,由此进行列主元QR分解所测向量矩阵的转置阵,有:
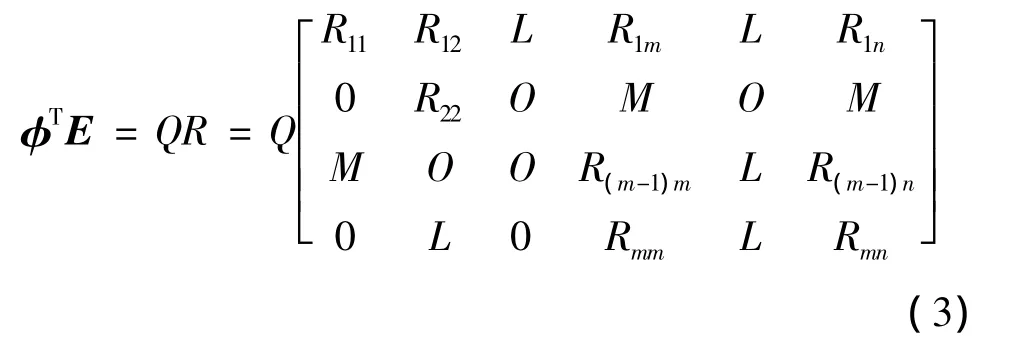
提取φ行向量组中具有较大范数的子集所对应的测点,这就为MAC法提供了初始的测点。
1.2.2 有效独立法
有效独立法首先构造矩阵E

该矩阵是目标模态矩阵φs所张成向量空间的投影矩阵。其对角元为:

ED的物理意义是给定传感器位置对目标模态矩阵φs线性独立性贡献的大小。通过ED值对各个候选测点的优先顺序进行排序,用迭代算法每次删除ED中最小的元素所对应的传感器位置,也即删除对目标模态矩阵φs独立性贡献最小的行,重新组成Fisher信息阵;再进行下一次迭代,再次删除一个位置,直到达到所需要的传感器数量为止,这就为侯选测点的选择提供了依据,保证了添加测点的线性无关性。
1.2.3 MAC 算法
为了避免由于向量与向量之间的交角偏小让系统无意损失关键模态的情况发生,MAC法作为一种保证准则来督促传感器的布置。其计算公式为:
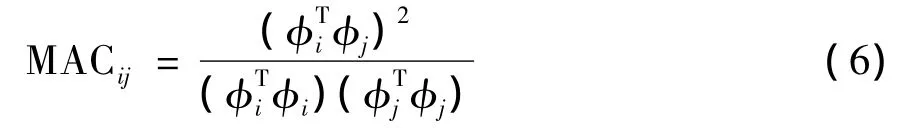
式中:φi和φj分别表示第i阶和第j阶的模态向量。这种督促方式下布置的测点应尽可能让MAC矩阵非对角元最小。设由列主元QR分解得到的初始配置结果为∈Rm×m,由结构的剩余自由度组成的振型矩阵子集为∈R(n-m)×m。当从中提取一行增加到中后,得到新的模态保证准则,其计算公式为:
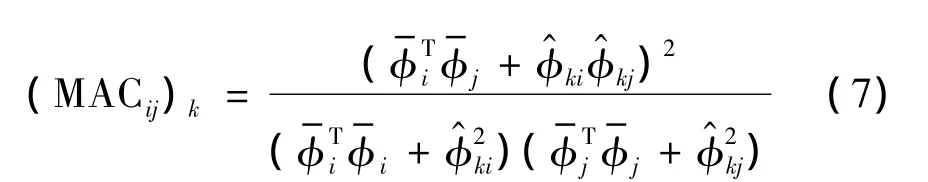
往已有测点组合里添加新的测点是一个反复迭代,不断寻优的过程,其根本目的是为了挖掘出使MAC矩阵中的最大非对角元减小得最快的测点。
运用此混合算法进行传感器布置的具体步骤是:
1)建立有限元模型,根据计算结果和所关心的振型特征,确定监测振型的具体模态,得到结构的模态向量矩阵,并确定传感器的布置数目;
2)对目标模态向量矩阵进行列主元QR分解,第1次获取布置传感器的初始测点位置;
3)利用有效独立法对模态向量矩阵(除去初始测点的模态向量矩阵)进行缩减,将测点的数量控制在已确定传感器的布置数量上下,并作为候选添加测点集合;
4)求得置信度MAC矩阵(由初始测点组成模态向量阵得来),并搜索出MAC矩阵中最大非对角元max;
5)随机选取第3步中确定的候选添加测点集合中一点添加到初始测点群中,计算模态向量阵的(MACij)k矩阵,其中k表示添加到测量自由度的自由度,并搜索出其最大非对角元maxk;
6)计算储存f(k)=maxk-max的值;
8)把添加了测点后的测点集合作为新的初始测点集合,然后反复运行步骤4)~7),直至得到理想测点数后退出程序;
9)简易的可视化处理——人为观察,淘汰位置比较近的测点,得到最终满足要求的测点,实现传感器优化布置。
其中,步骤1):利用Midas 2010对连续刚构桥进行建模和计算,并提取数据;步骤2)~8):利用matlab 7.1对已提取的数据进行编程。
2 工程实例
2.1 工程概况
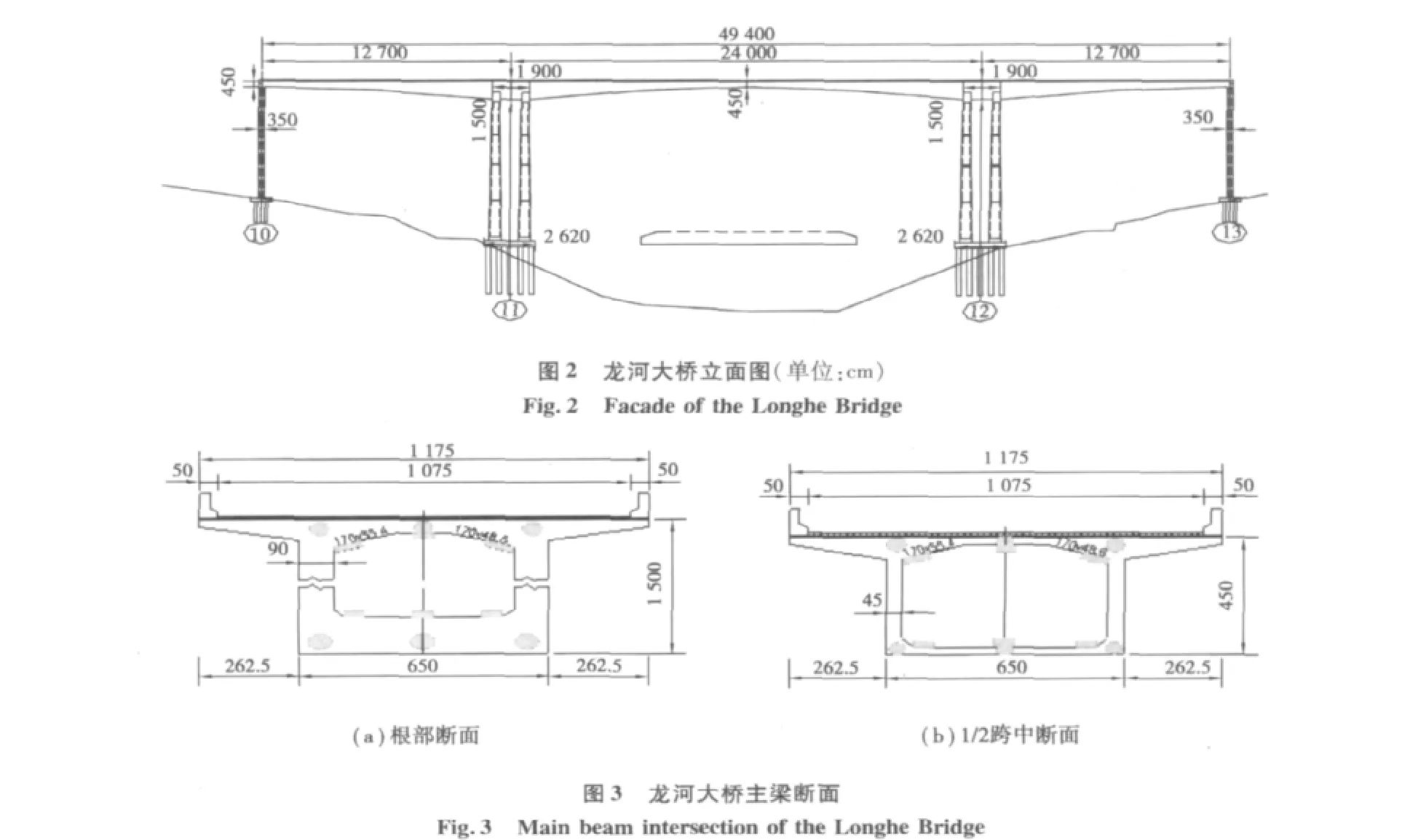
龙河特大桥位于重庆市丰都县三合镇东侧龙河上。主桥总长度为494 m,采用127 m+240 m+127 m三跨一联的预应力连续刚构,桥宽24 m,下部结构为双薄壁墩,最高墩高约116 m,桥面纵坡从左至右为-0.552%。设计车速为80 km/h,设计荷载为公路Ⅰ级,验算荷载为挂车特-300。全桥结构尺寸、断面分别如图2、图3。
2.2 模型的建立
采用大型桥梁专业分析软件MIDAS建立龙河特大连续刚构桥动力特性的有限元计算模型。其有限元模型根据桥梁实际尺寸建模,桥面(149个节点,按照浇段划分单元)、桥墩均采用三维梁单元,其有限元模型如图4。

图4 龙河大桥三维有限元模型Fig.4 Three-dimention finite element model of the Longhe Bridge
该连续刚构桥采用能充分利用M和K的稀疏带状性质的子空间迭代法[7]来对结构进行动力特性分析,求解其特征值方程。选择参加计算的频率数量为18,迭代次数为20,收敛误差为1E-10。得出龙河大桥的前18阶自振频率及其主振型。表1中只列出了前8阶自振频率、周期及振型特征,图5中给出了连续刚构桥前6阶的振型图。
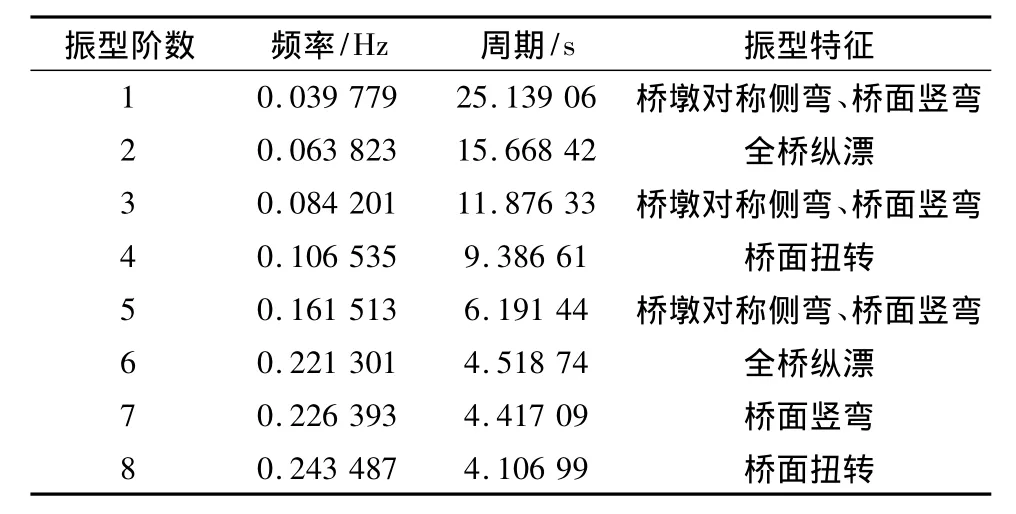
表1 自振频率、周期及振型特征Tab.1 Free vibration frequency and the vibration cycle and the vibration characters
2.3 测点的确定
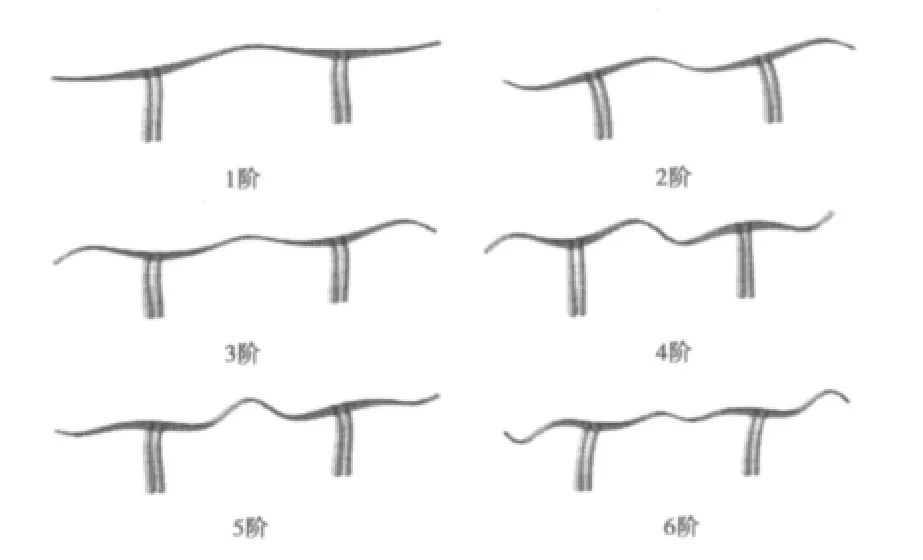
图5 龙河大桥1~6阶振型Fig.5 First to sixth vibration type of the Longhe Bridge
首先人为把监测的目标振型选定为6阶,这样不会浪费计算机的储存空间;其次选取龙河大桥的竖向振动特征作为有效振型;最后提取对桥梁的竖向振动有贡献的前6阶振型数据来考虑作为布置传感器的计算机程序原始数据。在表2中排名得到的前6阶竖向振型阶数为第1阶、第3阶、第5阶、第7阶、第9阶及第11阶,并将这6阶振型组成模态向量矩阵。然后采用列主元QR分解技术对模态向量矩阵进行分解,目的是找到使测量的模态向量保持较大空间交角的测点,在有限元模型上分别是节点75、7、84、15、94、26,如图 6(a)。然后采用有效独立法对剩余143个测点的模态矩阵进行筛选,依次删除前131个对目标模态矩阵独立性贡献最小的模态对应的测点,删除后剩余的测点为候选测点。接着采用MAC法,即每次从候选测点中选择一个点加入到初始测点群中,然后找出添加测点以后MAC矩阵中非对角元的最大值。重复以上过程,逐步让初始测点群收集到更多测点,并多次找出对应MAC矩阵非对角元的最大值,记录下来,把每一个这样的值作比较,其中最小者对应的测点有资格被添加到初始测点群。在每一次循环中,将添加测点后的测点集合当下一循环的初始测点群,直至找出所要布置的测点编号数。最终由此混合算法确定的节点号为7、14、15、25、26、66、75、84、85、94、124、135,如图 6(b)。最后根据可视化处理,保留靠得较近的测点之一,就可以得到最终的传感器布置方案[8],如图6(c)。
2.4 检 验
对应各种测点方案的MAC值如图7。通过观察,列主元QR分解得到的6测点较最终得到的12测点,后者的非对角元并没有增加,由此说明了添加测点过后得到的测量向量的空间交角比较好。
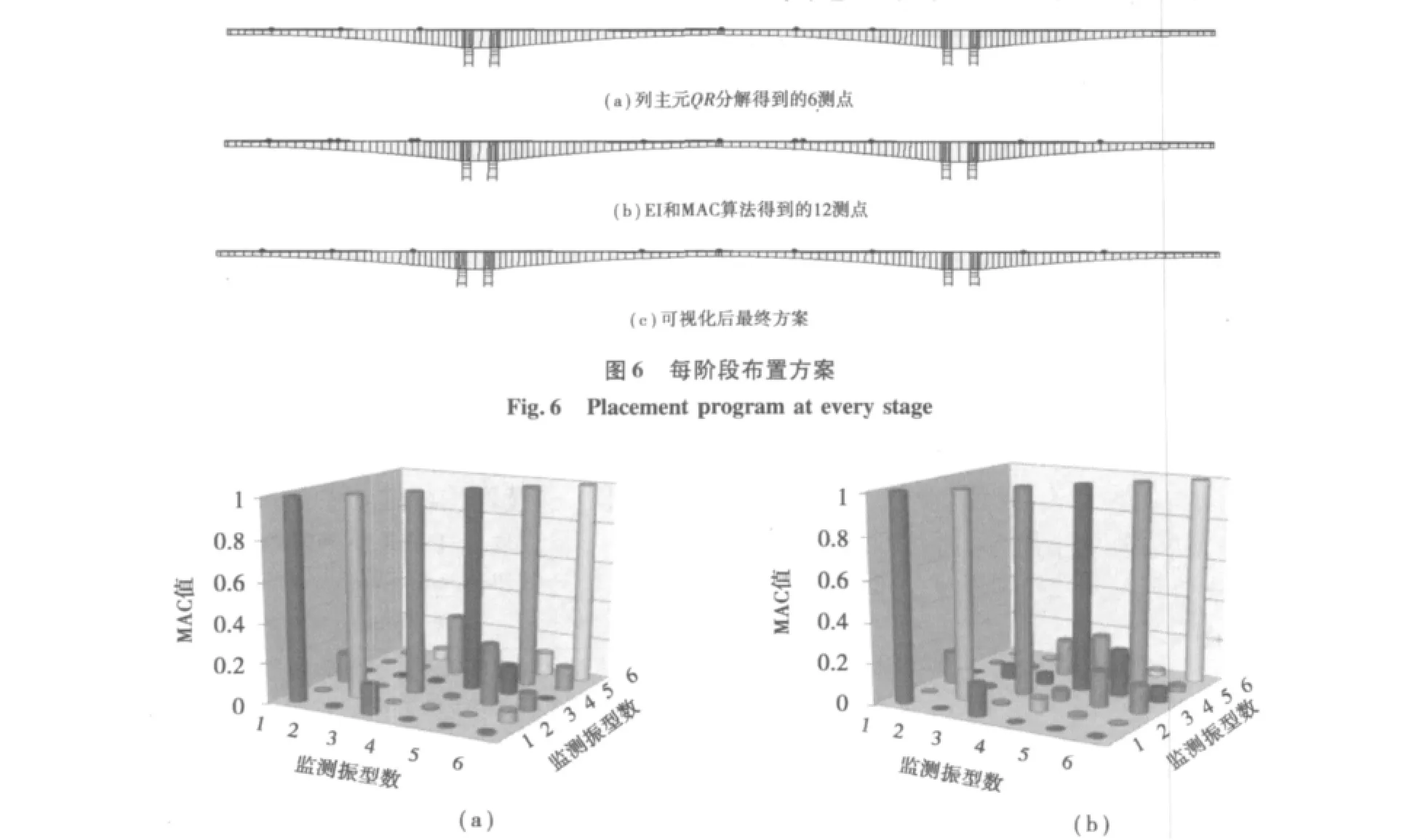
图7 MAC值2种布置方案的Fig.7 MAC value of the two layout programs
3 结论
从连续刚构桥的传感器优化布置研究得知,基于EI及MAC法得到的传感器布置点表现了所测数据的线性无关性和正交性,这正是汲取了EI法和MAC法优点的一种运用和体现;在对连续刚构桥的传感器布置过程中,避免人为凭借经验将传感器布置在根部、中跨1/4倍数截面、边跨1/4和边跨1/2截面等位置;从图7清晰显示的MAC非对角元素的情况来看,最开始的6测点和最后的12测点,反映数值的柱形体没有增加,这表明最终确定测点的振型空间交角比较好;由于连续刚构桥在根部受力复杂,建模时往往简化而不能准确反应根部特性,建议在实际工程中,无论是做荷载试验还是长期健康监测,首先考虑在根部附近布置传感器。
(References):
[1] 袁爱民,戴航,孙大松.基于EI及MAC混合算法的斜拉桥传感器优化布置[J].振动、测试与诊断,2009,29(1):55-59.
YUAN Ai-min,DAI Hang,SUN Da-song.Optimal sensor placement of cable-stayed bridge using mixed algorithm based on effective independence and modal assurance criterion methods[J].Journal of Vibration,Measurement& Diagnosis,2009,29(1):55-59.
[2] 袁爱民,戴航,李延和.EI法和MAC法在模态试验传感器优化布置中应用比较[J].工业建筑,2008(38):343-347.
YUAN Ai-min,DAI Hang,LI Yan-he.Application comparison of optimization of sensor placement in modal test using EI method and MAC method[J].Industrial Buildings,2008(38):343-347.
[3] Kammer D C.Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance,Control and Dynamics,1991,14(2):251-259.
[4] 秦仙蓉,张令弥.一种基于QR分解的逐步累积法传感器配置[J].振动、测试与诊断,2001,21(3):168-173.
QIN Xian-rong,ZHANG Ling-mi.Successive sensor placement for modal paring based on QR-factorization[J].Journal of Vibration,Measurement& Diagnosis,2001,21(3):168-173.
[5] 杨永贤,王福敏,周筠莉.城市轻轨连续刚构桥动力特性分析[J].公路交通技术,2007(2):94-97.
YANG Yong-xian,WANG Fu-min,ZHOU Yun-li.Analysis of dynamic behavior of continuous rigid frame bridge for urban light rail[J].Technology of Highway and Transport,2007(2):94-97.
[6] 赵小磊,李国普.悬索桥动力特性分析[J].规划与设计,2010(17):384-386.
ZHAO Xiao-lei,LI Guo-pu.Analysis on dynamic behavior of suspension bridge[J].Planning and Design,2010(17):384-386.
[7] 刘云,钱振东.润扬大桥北汊斜拉桥的动力分析模型和动力特性的研究[J].交通运输工程与信息学报,2006,4(1):99-103.
LIU Yun,QIAN Zhen-dong.Research on the analytical model and dynamic characteristics of the cable-stayed bridge of Runyang bridge[J].Journal of Transportation Engineering and Information,2006,4(1):99-103.
[8] 刘宇,毕丹,李兆霞.大跨斜拉桥基于遗传算法的传感器优化布置方法[J].东南大学学报,2009,39(4):825-829.
LIU Yu,BI Dan,LI Zhao-xia.Optimal placement of accelerometers in long cable-stayed bridges based on genetic algorithm[J].Journal of Southeast University,2009,39(4):825-829.
Optimal Sensor Placement of Continuous Rigid Frame Bridge Using Algorithm Based on Effective Independence and Modal Assurance Criterion Methods
HE Hua1,ZHANG Li-wen2,ZHOU Jian-ting2,YANG Jian-xi2,ZHOU Lei2
(1.Guangxi Ji Tai Investment Co.,Ltd.,Nan Ning 530203;
2.School of Civil Engineering & Architecture,Chongqing Jiaotong University,Chongqing 400074,China)
Function and applicability of effective independence method and modal assurance criterion method were introduced.A new hybrid algorithm by assembling their advantages was worked out;mathematical method was applied in optimal sensor placement of continuous rigid frame bridge on treat Longhe Bridge as a case.Result showed section location acquired after EI and MAC methods was different from root section and 1/4 times section in cross-border based on people’s experience.According to MAC,sensor placement of continuous rigid frame bridge could obtain satisfactory optimization result through the method.
effective independence method;modal assurance criterion(MAC);continuous rigid frame bridge;optimal sensor placement
U442.53
A
1674-0696(2011)05-0921-04
10.3969/j.issn.1674-0696.2011.05.008
2011-05-11;
2011-05-19
西部交通建设科技项目(200831895076);重庆市重大科技攻关项目(CSTC,2008RA6038)
何 华(1972-),男,广西桂平人,高级工程师,主要从事桥梁建设与维护技术研究。E-mail:hehua0283@sina.com。

