复合材料曲壁板与平壁板热颤振特性的对比
高 扬, 杨智春
(西北工业大学 航空学院,西安 710072)
壁板颤振是飞行器壁板结构在空气动力、惯性力和弹性力的耦合作用下产生的一种气动弹性不稳定现象,属于自激振动的范畴。早期的壁板颤振研究主要针对的是金属材料壁板,随着复合材料层合板在飞行器设计中的广泛应用,针对复合材料壁板颤振的研究得到了重视,由于层合复合材料壁板结构的特殊性,使得除了壁板的边界支持条件、气流偏角和几何尺寸外,复合材料壁板的铺层方式也是影响其颤振特性的一个重要因素。其中,铺层方式是设计中需要考虑的一个重要问题。
对于以高马赫数(一般大于2.2)飞行的飞行器,会产生明显的气动加热的效应。气动加热影响主要表现在改变材料机械性能和产生热应力两个方面,进而影响结构的颤振特性。对金属壁板的热颤振特性和热振动问题已经有不少研究[1,2]。
在实际飞机结构中,壁板是带有一定曲率的。初始曲率的存在会引入静态载荷,在大变形时会产生显著几何非线性刚度效应,在几何非线性引起附加的面内力、面内热应力和气动力的耦合作用下,曲壁板会呈现出更为丰富的非线性动力学现象,从而使得对曲壁板热颤振特性的研究具有重要的学术意义。Dowell[3,4]分别从定量和定性方面总结了曲壁板颤振的特性。Nagai等[5]针对平壁板和小曲率的曲壁板,进行了一些相关的试验研究。Azzouz[6]用非线性有限元方法进行了层合复合材料曲壁板的颤振分析,研究结果显示,曲壁板的初始曲率引入的静载荷将对曲壁板的颤振边界产生较大的影响,使得其颤振特性与平壁板有很大区别,但是他没有考虑铺层方式的影响。
国内已有关于铺层方式对复合材料平壁板热颤振的分析研究[7],铺层方式对复合材料曲壁板的颤振特性影响的研究还未见报道。本文提出了一种分析曲壁板热颤振特性的方法,通过对不同铺层角度和铺层顺序的层合复合材料曲壁板的热颤振分析,考察了不同铺层方式下曲壁板的颤振临界速度随温升的变化规律,对超音速气流中飞行器曲壁板的防颤振设计有一定的参考意义。
1 层合复合材料壁板内力与应变的关系
考虑图1所示圆柱壳曲壁板,其总应变为中面位移产生的应变、考虑大变形时挠度引起的面内附加应变、弯曲产生的应变和曲板初始拱高h0(x,y)引起的Marguerre 应变的和[6]:
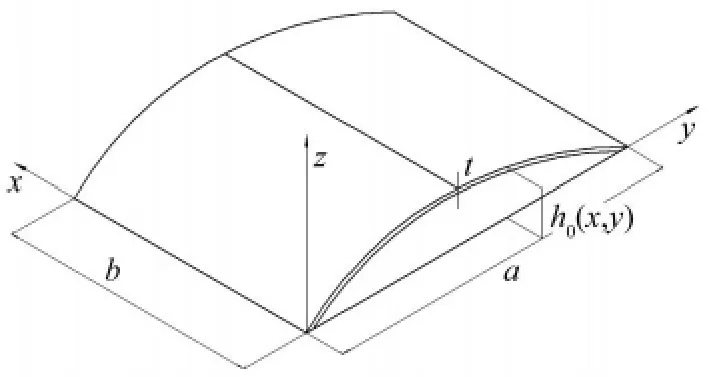
图1 曲壁板的坐标系定义Fig.1 Coordinates of curved panel model
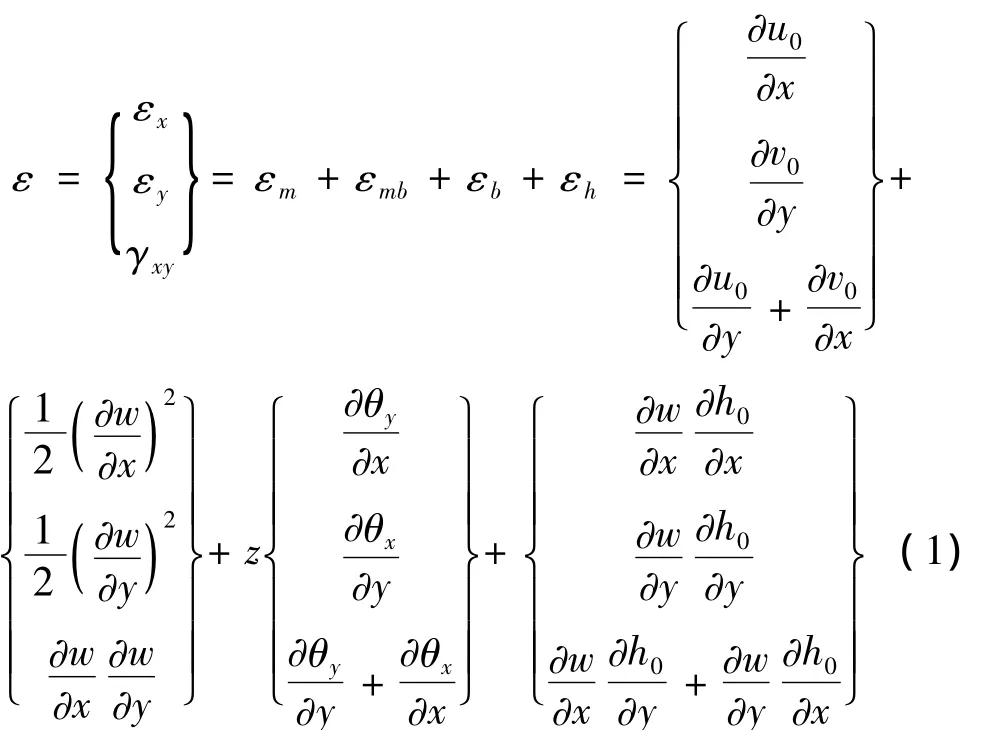
横向剪切应变为:
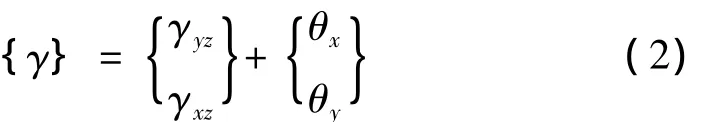
其中,u0,v0,w0为中面位移,θx和 θy为中面分别绕 x 轴和y轴的转角。
令 ε0=εm+ εmb+εh,则层数为 NL的复合材料层合板单位宽度上的内力表达式可写为:
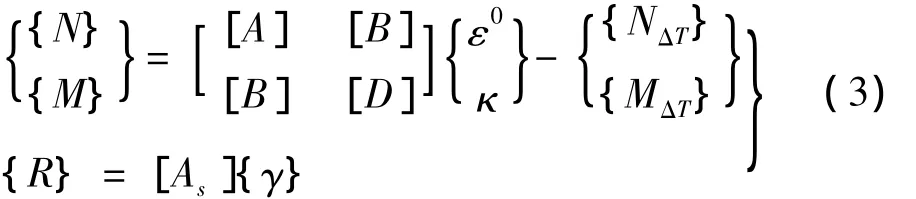
其中:
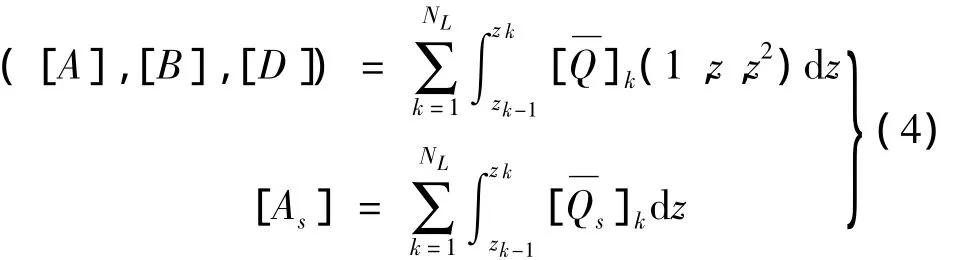
式中:[A]为拉伸刚度矩阵,[B]为耦合刚度矩阵,[D]为弯曲刚度矩阵,[As]为剪切刚度矩阵,[]和[]为偏轴刚度矩阵,{N}{M}和{R}分别为单位宽度上层合板的平均面内力、平均面内力矩和平均横向剪切力,{NΔT}和{MΔT}为温度场引起的载荷。
对于平壁板[7],其应变及应力公式与曲壁板类似,只需从总应变(1)式中删去由于曲壁板任意点处初始拱高h0(x,y)引起的Marguerre应变εh项。
2 层合复合材料壁板热颤振分析
2.1 层合复合材料壁板热颤振方程
考虑如图1所示圆柱壳曲壁板,气流沿x轴方向,曲壁板表面的气动力可由一阶活塞理论求得[6]:
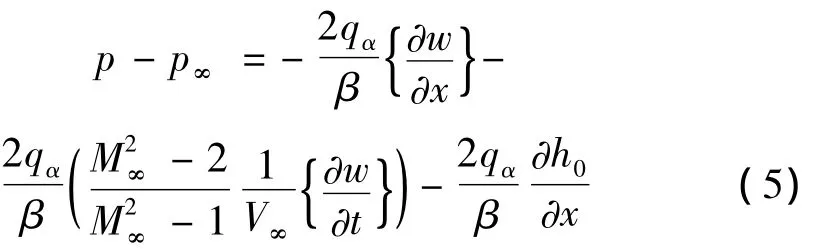
根据曲壁板的内力与应变关系,由虚功原理可得超声速气流中受热曲壁板运动方程[6]:
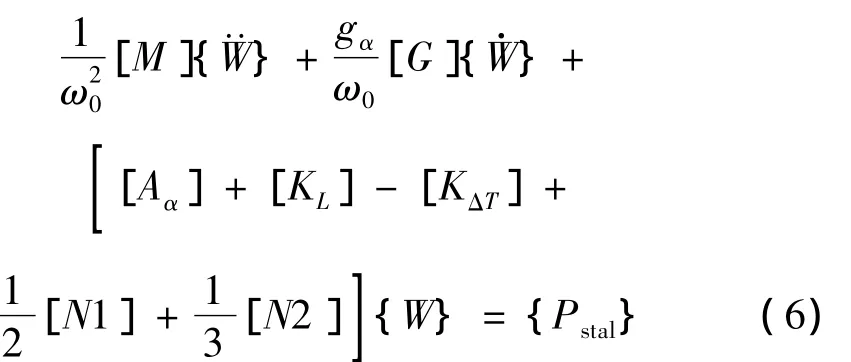
其中静态载荷向量{Pstal}为:
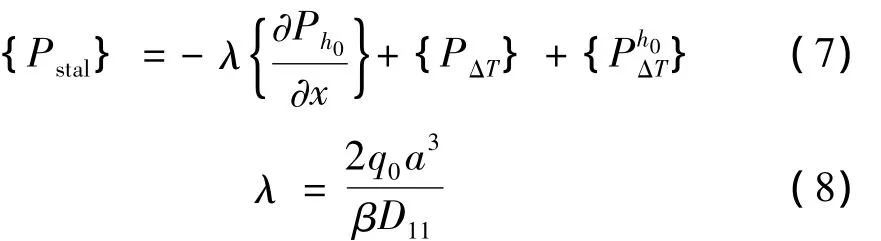
式中:[M]为系统的质量矩阵,[G]为气动阻尼矩阵,[Aα]为气动刚度矩阵,[KL]为系统线弹性刚度矩阵,[KΔT]为热载荷引起的线性刚度矩阵,[N1]和[N2]分别为系统的一阶和二阶非线性刚度矩阵,{W}为结点位移向量,为由曲壁板初始拱高h(x,y)引起的0静气动载荷{Ph0}在x方向的分量,{PΔT}为热载荷向量,{}是与曲壁板初始拱高h0(x,y)有关的热载荷向量。无量纲气流参数λ定义式中,D11为复合材料曲壁板弯曲刚度矩阵D的第一个对角线项D(1,1),a为曲壁板在气流方向长度。
对于平壁板的热颤振分析[7],运动方程右端应删去与曲壁板初始拱高h0(x,y)有关的项。
曲壁板的位移响应可以看作由静变形{W}s和动变形{W(t)}t两部分的线性叠加构成:
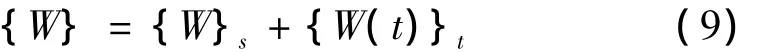
{W}s不随时间变化,是曲壁板在气动力载荷和热载荷共同作用下处于静力平衡时的变形;{W(t)}t是时间的函数,刻画了一个与时间相关的自激振动,描述了曲壁板随时间变化的动态特性。
2.2 壁板热颤振分析过程
在壁板的热颤振分析中通常采用两个简化假设:① 壁板结构的变形不影响温度场;② 颤振响应的时间尺度远小于温度变化的时间尺度,因此在壁板的热颤振分析中可以将温度场看作是稳态的;③ 在温升不太高的情况下忽略温度对材料特性的影响。
本文的热颤振分析求解分为两个过程。首先建立带有热载荷的壁板有限元模型,通过非线性分析将因热载荷而引起的结构附加刚度引入到结构总体刚度中,得到结构的等效刚度矩阵。
之后采用p-k法求解超声速气流中受热曲壁板颤振方程。求解时需要预先给定一系列速度V,通过迭代来得到结果。
按照上述求解过程,就可以完成考虑结构的热壁板颤振分析。
3 复合材料曲壁板与平壁板热颤振特性对比
层合复合材料可以利用不同铺层方式得到所需要刚度特性的层合板。工程上经常使用的层合板往往是一些具有特殊铺层方向和铺层顺序的层合板,如正交铺设对称层合板、斜交铺设对称层合板、准各向同性层合板和一般π/4层合板等。本节将考虑两种准各向同性层合板和一种正交铺设对称层合板,其铺层方式分 别 为 [ 0/- 45/45/90]s、[0/- 45/90/45]s和[0/90/90/0]s,单层厚度为 0 .15 mm,铺层的材料性能见表1。圆柱壳曲壁板的初始最大拱高,在xy平面投影面的几何尺寸为0.381 m×0.305 m,为了进行对比,平壁板几何尺寸就取为曲壁板xy平面的投影几何尺寸。两类壁板的边界条件均为四边固支,气流方向沿x轴。
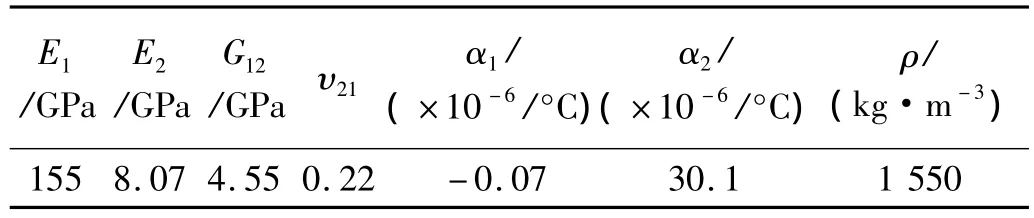
表1 石墨/环氧材料的力学性能参数表Tab.1 The Material Property
3.1 受热曲壁板与平壁板的动力学特性
分别计算三种不同铺层方式曲壁板CP1、CP2、CP3和平壁板FP1、FP2、FP的前六阶固有频率随温升的变化曲线,以对比分析不同铺层方式曲壁板和平壁板的动力学特性。三块平壁板的屈曲临界温升分别为:
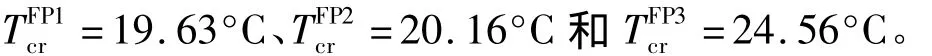
由图2(a)可见,随着温度升高,平壁板的前六阶固有频率随温升的增大都有明显的下降趋势,这是因为壁板刚度随着温度升高而降低,即出现所谓的刚度“软化”现象。FP1和FP2的第一、三、四、六阶频率基本相同,第二阶频率差别较大。FP3与FP1、FP2铺层角不同,铺层顺序亦不同,前六阶固有频率相差较大。FP3为正交铺设对称层合板,只由0°和90°两种角度的单层板铺成,在三种不同铺层方式中这种铺层方式下的前六阶频率最高,说明顺气流的0°铺层和垂直于气流的90°铺层对刚度贡献大。
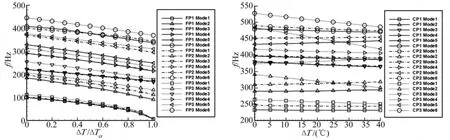
图2 (a)平壁板固有频率随温升变化(b)曲壁板固有频率随温升变化Fig.2 (a)Variation of the natural frequencies of the flat panels versus temperature(b)Variation of the natural frequencies of the flat panels versus temperature
而曲壁板不存在临界屈曲温升。由图2(b)可见,曲壁板CP1和CP2的铺层角相同,铺层顺序不同,其固有频率随温升的变化情形相似,第二阶和第五阶固有频率随温度升高而升高,其余阶固有频率随温升基本不变,且第三、四、六阶固有频率基本相同,第一、二、五阶固有频率差别较大。CP3的第一、二、六阶固有频率随温度升高而下降,第三、四、五阶固有频率随温升先有趋近的趋势,之后第四、五阶固有频率略有升高,而第三阶固有频率降低趋势明显。
由于复合材料曲壁板固有振动特性随铺层方式和温升的变化与平壁板有明显不同,可以推断出它们颤振特性也会有较大不同。下面针对这三种铺层方式的曲壁板和平壁板进行热颤振分析对比,以获得铺层方式和温升对其颤振速度的影响规律。
3.2 复合材料曲壁板与平壁板热颤振特性的对比
设定飞行的海拔高度为8km,对应的大气密度为0.525 kg/m3,当地声速为 308.06 m/s。分别计算得到三块不同铺层方式的复合材料曲壁板和平壁板在温升分别为0°C~40°C时和温升为0~ΔTcr时的热颤振临界速度随温升的变化曲线,如图3所示。
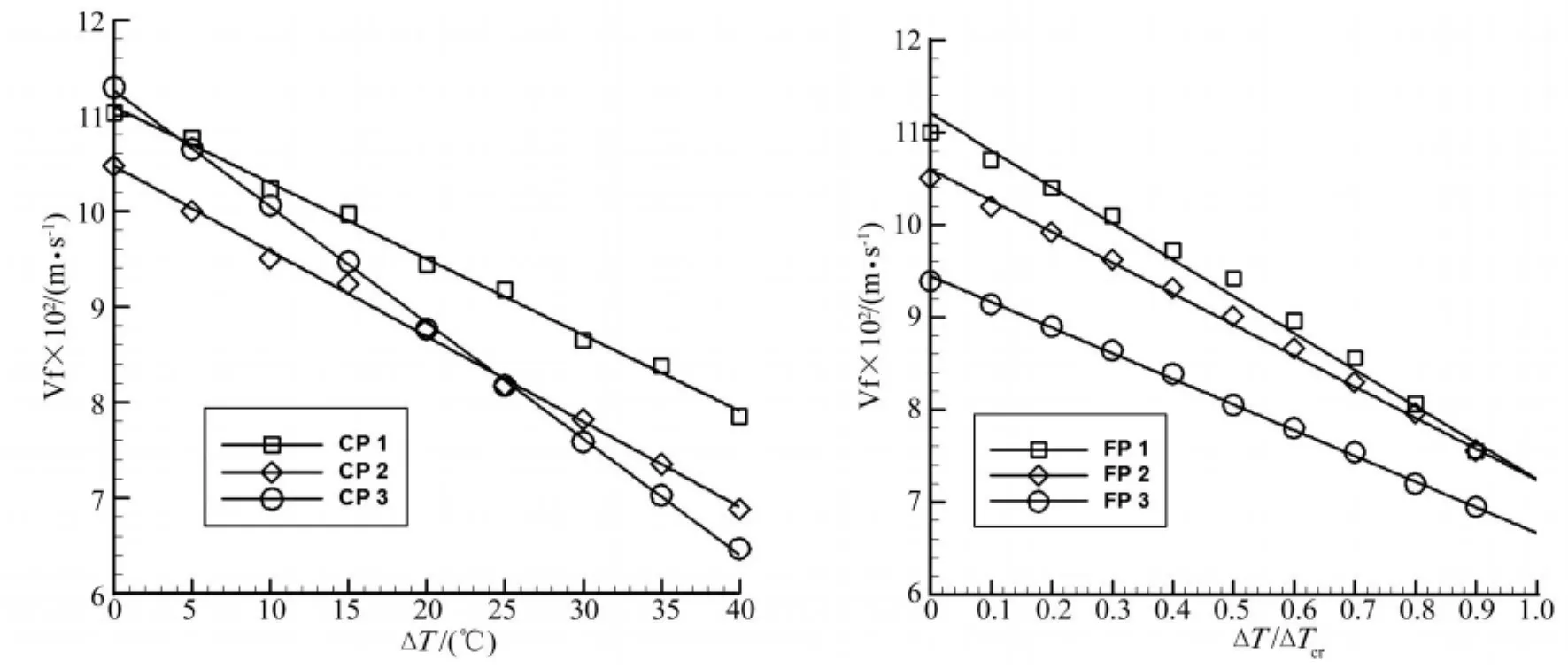
图3 (a)曲壁板颤振临界速度随温升变化(b)平壁板颤振临界速度随温升变化Fig.3 (a)Variation of the critical flutter velocity of the curved panels versus temperature(b)Variation of the critical flutter velocity of the flat panels versus temperature
由图3可以看到:
当ΔT=0°C时,CP1、CP2和CP3的颤振临界速度分别为 1102.94 m/s、1047.06 m/s 和 1129.41 m/s,即。CP1和CP2的铺层角度相同,顺序不同,CP1准各向同性的铺层方式在无温升时的颤振临界速度比CP2大5%,可见曲壁板的颤振速度对铺层顺序的变化比较敏感;正交铺设层合板CP3与准各向同性铺设层合板CP1、CP2的铺层角度和铺层顺序都不同,无温升时的颤振临界速度最高,颤振特性最好。
当ΔT=0°C时,FP1、FP2和FP3的颤振临界速度分别为1103.03 m/s、1048.10 m/s和 938.98 m/s,即。FP1是准各向同性铺设的层合板,它在研究温升范围内始终保持最大的颤振临界速度。虽然FP2和FP1的铺层角度相同,但是铺设顺序不同,两者的动力学特性亦不同,如图3所示。FP3与FP1、FP2的铺层角度和铺层顺序都不同,虽然它的前三阶频率均为最高,但是颤振速度最低。
当ΔT=0°C时,对于准各向同性铺设方式的复合材料,曲壁板和平壁板的颤振临界速度几乎相同;对于正交铺设方式的复合材料,曲壁板的颤振临界速度比平板提高20.28%。
对于三种铺层曲壁板和平壁板,颤振临界速度随温升近似呈线性下降关系。其中,准各向同性平壁板的颤振临界速度在温度接近各自临界屈曲温度时趋于同一值,正交铺设方式板并不存在此现象。壁板发生热屈曲时,与屈曲模态相关的刚度完全丧失,其他阶模态刚度仍存在。对于上述现象中的准各向同性平壁板,因为其参与颤振的模态和屈曲模态相同,在温度接近各自临界屈曲温度时仅剩气动刚度,所以颤振临界速度趋于同一值。然而正交铺设方式板参与颤振的模态与屈曲模态不同,所以不会出现类似现象。
三块曲壁板和平壁板颤振临界速度相对于温升的变化率分别为 7.94 m/(s·℃-1)、8.97 m/(s·℃-1)、12.06m/(s·℃-1)和 19.58m/(s·℃-1)、16.24 m/(s·℃-1)、11.02 m/(s·℃-1)。从温度载荷对曲壁板颤振临界速度的影响来看,CP1和CP2的变化率显著小于CP3,即与准各向同性铺设的曲壁板相比,正交各向异性铺设的曲壁板刚度随温升“软化”程度更大。对于平壁板而言,从颤振临界速度相对于温升的变化率来看,FP3的颤振速度对温升最不敏感,也就是说,与准各向同性的铺设方式相比,正交各向异性铺设的平壁板“刚度软化”程度更小。相同铺层方式下曲壁板与平壁板比较,颤振临界速度相对于温升的变化率分别降低了71.91%、69.83%和25.59%,即曲壁板“刚度软化”程度更小。从图3壁板固有频率随温升变化曲线看出,在温升中曲壁板的各界固有频率始终大于平壁板,即前者的刚度一直大于后者。
对曲壁板来说,准各向同性层合板CP1和CP2的颤振临界速度相对于温升的变化率小于正交各向异性层合板CP3的值;平壁板中,情况正好相反。即对于曲壁板,与正交各向异性的铺设方式相比,准各向同性的铺设方式“刚度软化”程度更小;对于平壁板,情况正好相反。
通过考察曲壁板和平壁板参与颤振耦合的危险模态可知,对于曲壁板,CP1和CP2的的固有模态振型相同,CP3与前二者不同;而对于这三种不同铺层方式的复合材料平壁板,其固有模态振型并未随铺层方式不同而改变。这说明在铺层角度相同时,铺层顺序对曲壁板和平壁板的固有模态振型都没有较大影响;不同的铺层角度和铺层顺序会改变曲壁板的固有模态振型。曲壁板CP1、CP2的铺层角度相同,铺层顺序不同,其颤振都是由其第五、六阶模态发生耦合所导致的;CP3与CP1、CP2的铺层角度和铺层顺序都不同,其颤振是由第三、四阶模态发生耦合引起的。可见,曲壁板的铺层角成分会影响参与耦合的危险模态。对于平壁板,其颤振都是由第一、二阶模态发生耦合所导致的,即铺层方式的不同不会影响参与耦合的危险模态。
通过以上分析可知,对于相同铺层方式的曲壁板与平壁板,热颤振边界及参与颤振耦合的模态均不相同,原因有二:① 曲壁板的几何曲率使其弯曲刚度比相同投影几何尺寸的平壁板弯曲刚度大;② 在同时考虑气动力和热效应的情况下,曲壁板的初始几何曲率同时引入了静态气动载荷和静态热载荷,由于这些静态载荷的存在,在颤振发生前曲板将存在一定的静气动变形和静态热变形,使得曲板的总变形是静态变形和动态变形两部分的叠加。正是这些静态载荷和静变形的存在,使得曲板的颤振特性与平板有很大不同。
4 结论
通过考虑热效应影响对三种不同铺层方式的复合材料曲壁板和平壁板热颤振特性的对比分析,得到了其颤振临界速度随温度的变化规律。结果表明:
(1)温升会导致壁板颤振临界速度随温升近似呈线性下降,正交各向异性铺设的曲壁板与准各向同性铺设的曲壁板相比,其颤振临界速度下降得更快一些,而平壁板情况刚好相反;
(2)不同铺层方式曲壁板的热颤振危险模态不同,而平壁板热颤振危险模态不受铺层方式的影响;
(3)随温度升高,不论对于平壁板还是曲壁板,采用[0/-45/45/90]s铺层方式的热颤振特性相对较好。
[1]Chang W P,Jen S M.Nonlinear free vibration of heated orthotropic rectangular plates[J].Int.J.Solid Structure,1986,22(3):267-281.
[2]Chang W P,Wan S M.Thermo mechanically coupled nonlinear vibration of plate[J].Int.J.Non-Linear Mechanics,1986,21(5):375-389.
[3]Dowell E H.Panel flutter:A review of the aeroelastic stability of plates and shells[J].AIAA Journal,1970,8:385 -399.
[4]Dowell E H.Non-linear Flutter of Curved Panels[J].AIAA Journal,1969,7(3):424 -431.
[5]Nagai K,Maruyama S.Experiments and analysis on chaotic vibrations of a shallow cylindrical shell-panel[J].Journal of Sound and Vibration ,2007,305:492 -520.
[6]Azzouz M S.Nonlinear flutter of curved panels under yawed supersonic flow using finite elements[D].Old Dominion University,Norfolk,VA,2005.
[7]杨智春,等.铺层方式对复合材料壁板热颤振特性的影响[J].宇航学报,2008,29(3):1047-1052.

