基础简谐激励下匀速旋转运动电流变夹层梁的振动稳定性
魏克湘,孟 光,张文明
(1.湖南工程学院 机械系,湖南 湘潭 411101;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
电流变夹层结构由于能在外加电场的作用下,快速可逆的调节自身的阻尼和刚度,在结构的振动控制中获得了广泛的关注。自20世纪80年代Gandhi等[1]最早开始对电流变自适应结构进行研究以来,已有许多学者对其进行了深入的理论和实验研究[2-5]。但在以往的研究中,一般都是针对静态梁或板进行的,有关电流变材料应用于运动柔性梁振动控制的研究报道还较为少见。在先前的研究中[6-8],我们将电流变夹层结构推广应用到旋转柔性机械臂的振动控制,对电流变夹层结构梁在定速和周期变速运动条件下的动力学特性进行了研究,发现可以通过控制作用于电流变夹层结构梁上的电场强度来调节旋转柔性梁的振动特性,提高结构的动力稳定性。
对于柔性机械臂等旋转系统,除了结构本身的运动外,其支撑往往也是运动的。同时,在对作大范围运动弹性结构的动力学行为研究中,通常也可以将其简化为一个受定轴转动与基础激励联合作用的系统来近似模拟[9,10]。故研究基础激励作用下定轴转动柔性梁的动力学行为具有重要的理论意义和应用价值,许多学者对其进行了研究[11-14],但一般都是针对 Euler梁或Bernoulli梁进行的,而对复合材料或夹层结构梁的分析还较少涉及。
本文将对基础激励作用下旋转运动电流变夹层梁的动力学特性和振动稳定性进行分析。首先利用多尺度法建立受基础激励作用的旋转运动电流变夹层梁的一次近似方程,得到系统可能发生参激共振失稳的条件。然后通过对匀速旋转电流变夹层梁在不同激励参数、控制电场和旋转速度时的振动响应特性的分析,探讨受电场控制的电流变夹层梁在基础激励与定轴转动联合作用下的动力学特性和振动稳定性。
1 动力学建模
图1为一受基础激励作用的旋转运动电流变夹层梁结构示意图,其中坐标系XYZ为固定参考系,X1Y1Z1为固结在中心刚体上的浮动基。假设电流变夹层梁随中心刚体一起绕O1点作角速度为θ·的定轴旋转运动,与此同时,中心刚体受基础激励的作用在固定坐标系OXY中作直线(往复)运动,其运动规律在X方向和Y方向分别为x(t)与y(t)。
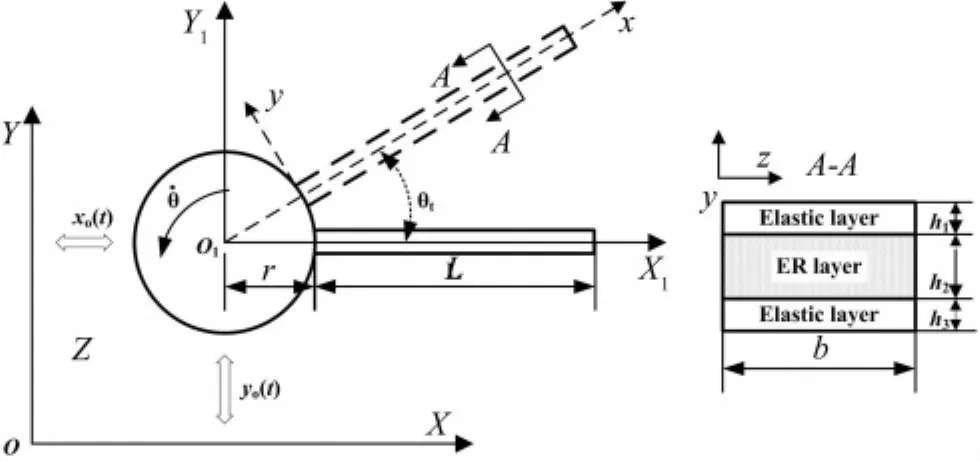
图1 受基础激励作用的旋转运动电流变夹层梁Fig.1 A rotating sandwich beam embedded with ER fluids subjected to base excitation
设中心刚体在运动起始位置时O1点与静止坐标系原点O重合,且假设梁只在面内产生运动,则可得到中心刚体在惯性参考系中的线速度和角速度分别为。将上述关系式代入文献[10]中的式(3.15)及式(3.16)~(3.40)中,得到非惯性系下基础激励与定轴转动联合作用时电流变夹层梁的动力学控制方程为:
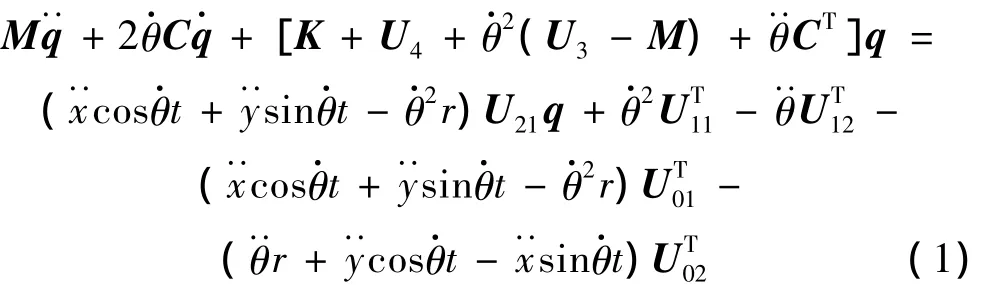
其中:
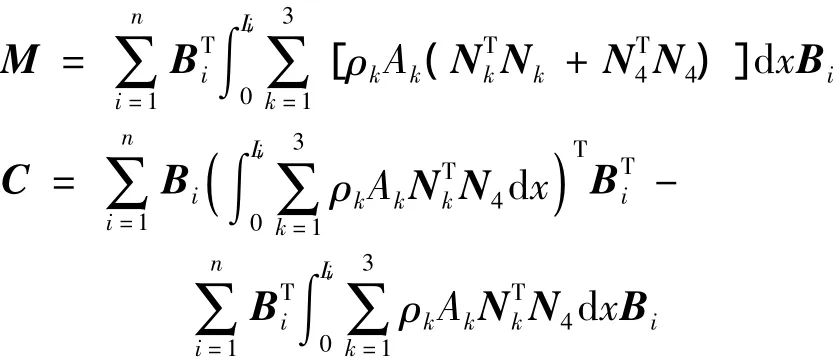
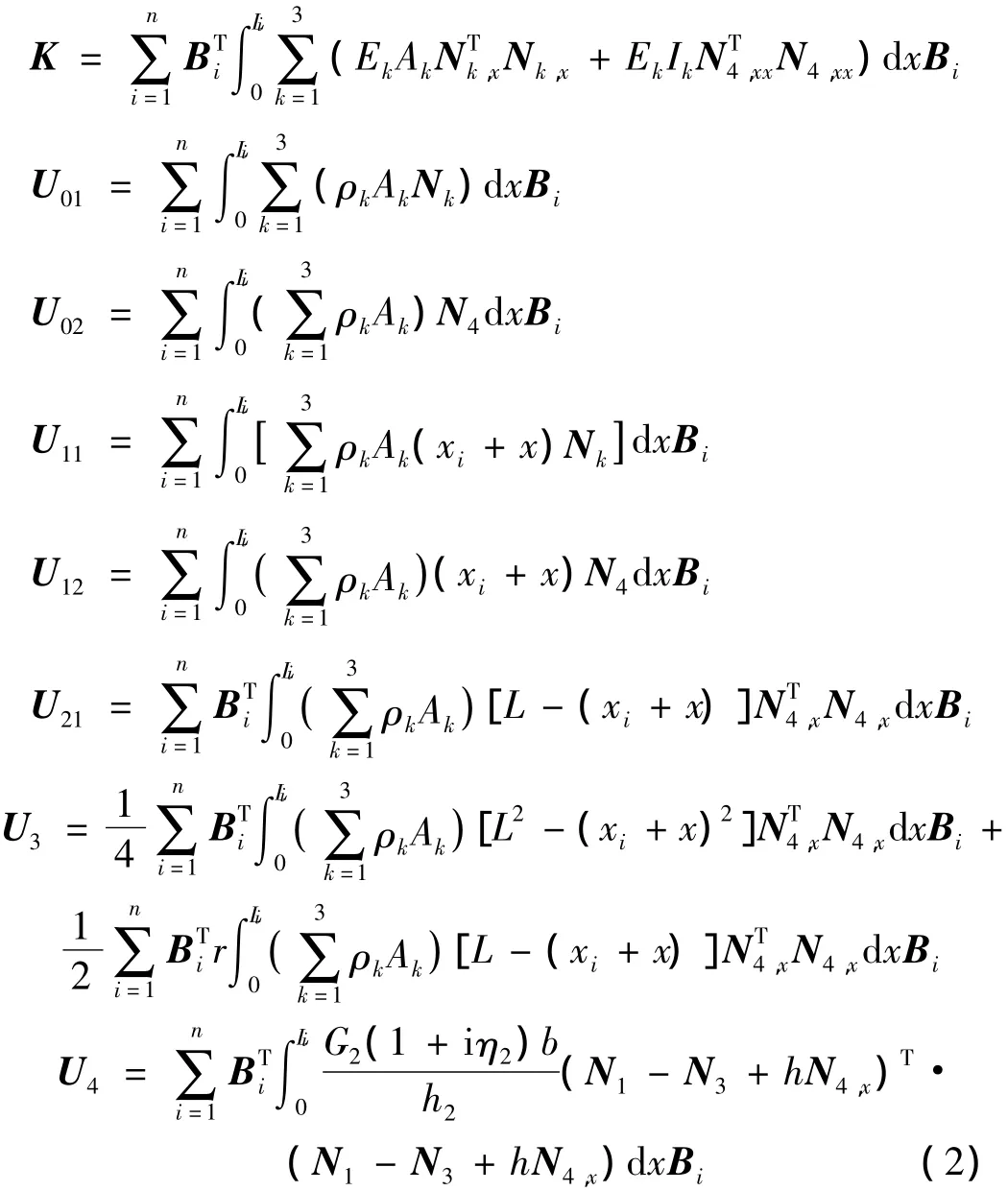
上列各式中,ρk、Ak、Ek、Ik(k=1,2,3)分别为夹层梁中各层的材料密度、横截面面积、弹性模量和转动惯量;G2为电流变材料的储能模量,η2为电流变材料的损耗因子;L为梁的长度,n为有限元单元个数,Li=L/n为单元长度,r为中心刚体的半径,xi代表梁的固支点到第i个单元左边节点的距离;ζ=x/Li,下标(,x)表示对 x 求导;N1、N2、N3和N4为对应单元节点位移的形函数矩阵,且:
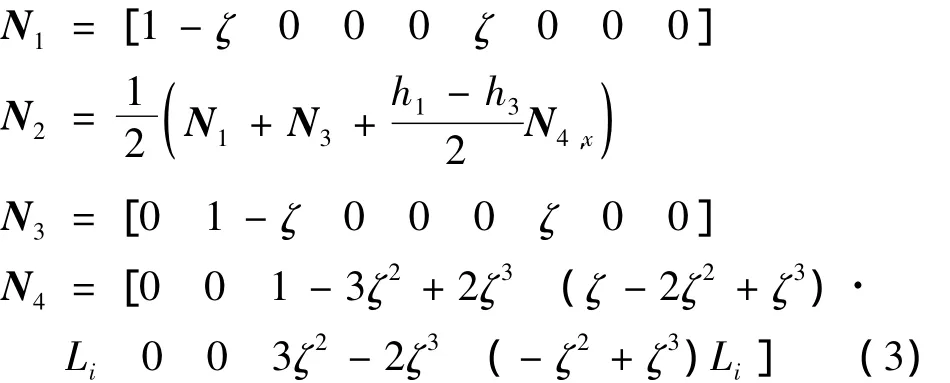
Bi为由梁单元编号决定的布尔(Boole)指示矩阵:
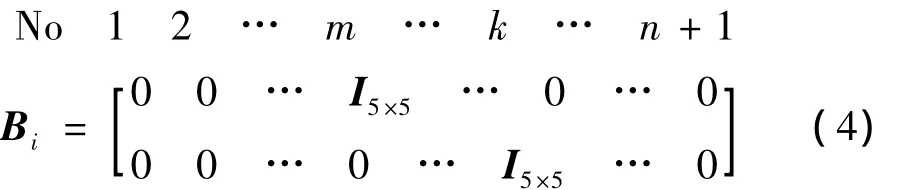
假设刚性转轴中心O1沿X方向的直线运动规律x(t)=0,沿Y方向的直线运动位移,其中y0及分别为简谐激励位移的幅值及其角频率,故基础激励的速度和加速度分别为。若只考虑梁作匀速转动,则式(1)可以简化为如下形式:
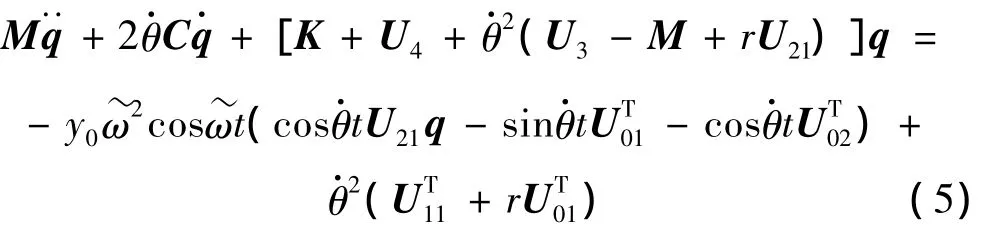
引入线性变换ξ=Φq,Φ为上式派生系统的正则振型矩阵,利用振型矩阵的正交关系,对式(5)中的质量和刚度矩阵解耦,得到:
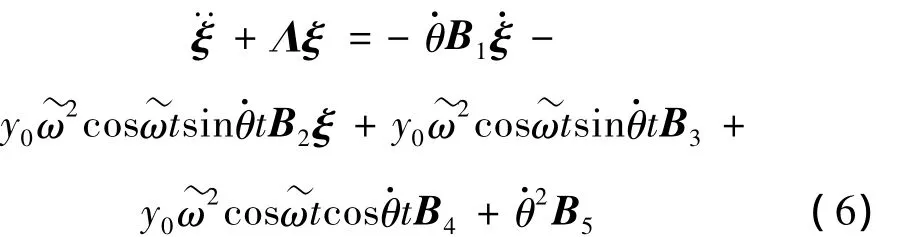
其中:
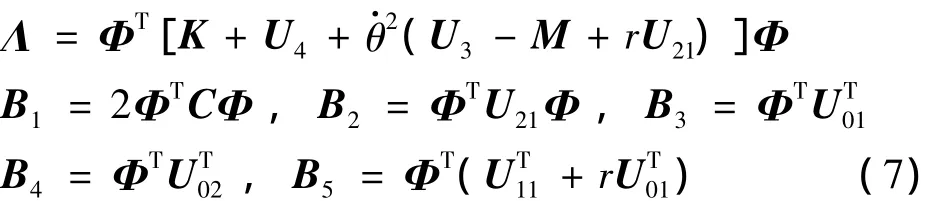
2 一次近似展开
假设刚性转轴中心的加速度并不大,将陀螺效应矩阵C,即式(6)中的矩阵B1也表示为小量参数的函数,则式(6)可表达为:
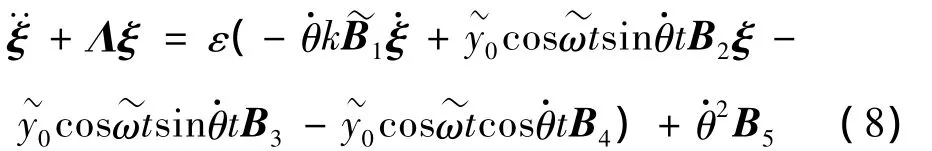
采用多尺度法将解展开为:
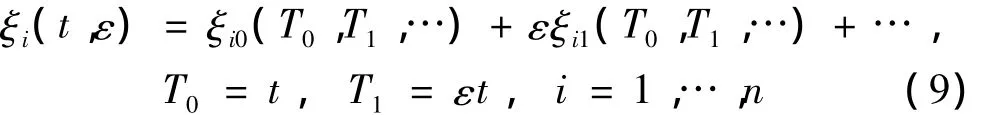
代入式(8),对其进行一次近似展开并令ε0及ε1前的系数为零,得到:
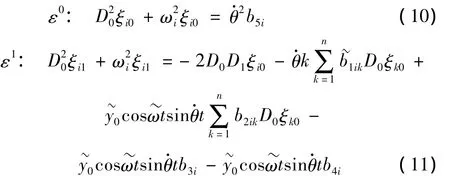
式(10)的解可写成:
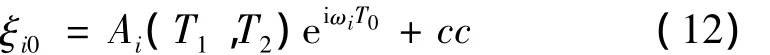
式中cc代表前项的共轭。将其代入式(11),经整理得:
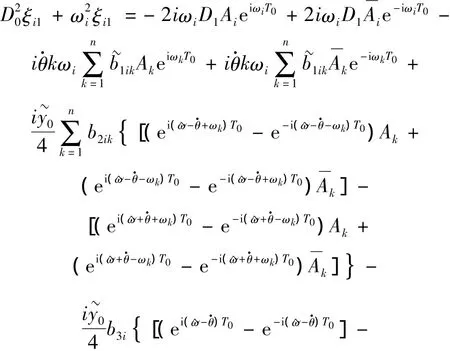
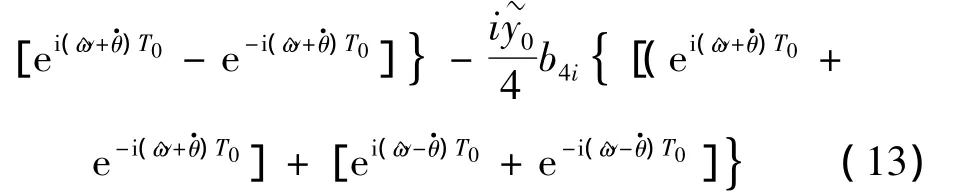
上式中的指数项不仅包括系统的固有频率ωp和ωq,还含有梁的转动频率。当基础激励频率~ω满足:
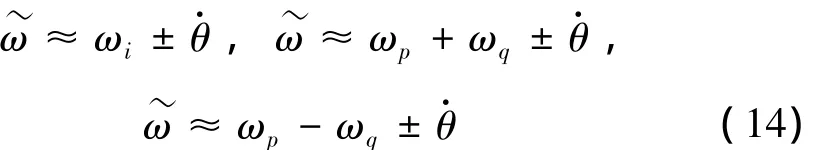
时,式(13)的右边将出现永年项,系统可能发生参激振动失稳现象[15,16]。
3 参激振动响应
我们可以对式(5)采用Runge-Kutta方法直接计算其在基础激励频率~ω满足式(14)中的条件时的振动时域响应特性,来分析各种结构和外加控制参数对受基础激励作用的旋转运动电流变夹层梁在发生参激共振时的动力学特性和振动稳定性的影响规律。梁的基本参数设定为:长度L=300 mm,宽度b=20 mm,表面弹性层的厚度h1=h3=0.5 mm,电流变材料层的厚度h2=2 mm;表面层材料的质量密度ρ1=ρ3=2800 kg/m3,弹性模量E1=E3=70×109Pa;电流变液的质量密度ρ2=1400 kg/m3,储能模量 G'=1500 E,损耗因子 η2=0.27E+3.73,其中E为外加电场强度。
首先我们讨论受电场作用的转动梁在不同基础激励幅值下的参激振动响应特性。假设转动速度=500 r/min,外加电场强度E=1 kV/mm,(0)=0,q(0)=0,考虑基础激励频率及时,对应不同激励幅值y0的梁端点的横向振动响应时间历程及其相图如图2~图4所示,从图中我们可以得到以下结论:
(1)当基础激励的幅值很小时,由于在电场作用下,夹层梁中的电流变材料具有粘弹性阻尼材料的特性,系统存在耗散力,梁的振动幅值先随时间衰减,而后在平衡点附近作微幅周期运动,系统存在稳定的周期解,如图2(a)所示。
(2)在一定的取值范围内,增大基础激励的幅值,仅仅改变振动响应幅值的大小,而对系统的振动特性不会产生影响,如图2(b)所示。
(3)当激励幅值增大到某一值后,系统的运动状态将发生变化。系统除作高频微幅周期振动外,还存在一个低频的周期运动。但整体振动幅值是在有限范围内变化,系统还是稳定的,如图2(c)所示。
(4)继续增大激励幅值,系统将进入不稳定状态,出现参激共振失稳现象。如图2(d)、图3(b)和图4(b)所示,此时梁的振动幅值随时间无限增大,系统失稳。
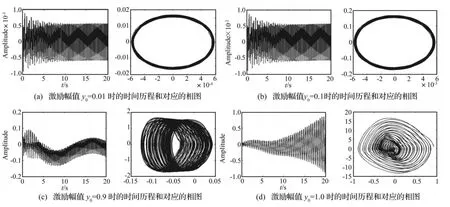
图2 第一阶主参激共振时的响应特性:E=1 kV/mm,=500 r/minFig 2 Response of the first principal resonance at E=1 kV/mm and=500 r/min
(5)系统的第二阶主参激共振和第一、二阶组合参激共振具有与第一阶主参激共振情况下基本相同的特性,即随着激励幅值的增大,系统将由作有限幅值的稳态周期运动逐步过渡到不稳定状态。只不过系统发生参激共振失稳的临界激励幅值显著减小,且在第二阶主参激共振时达到最低。如图3(b)和4(b)所示,当激励频率和时,出现不稳定解的临界激励幅值分别为y0=0.135与y0=0.16,而在时,对应的y0=1.0。
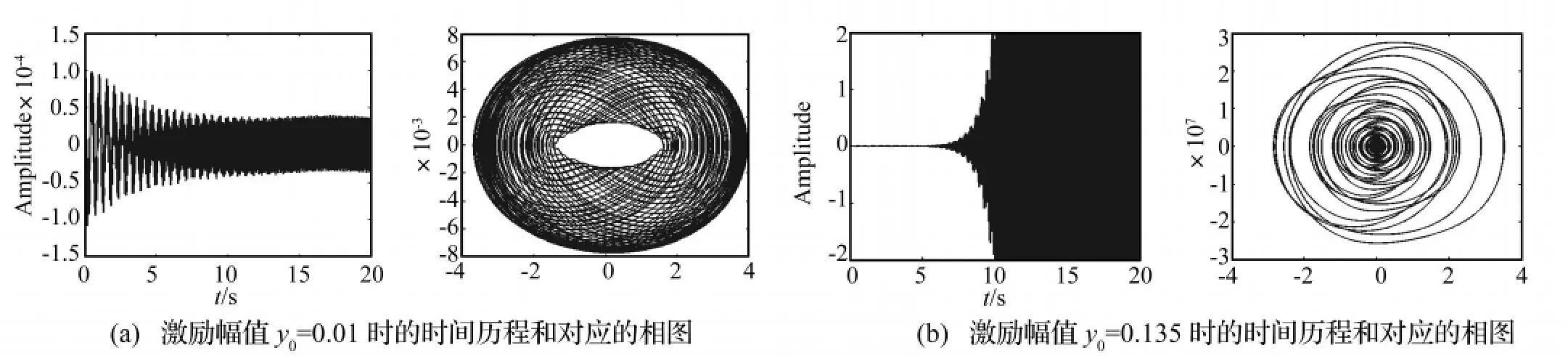
图3 第二阶主参激共振时的响应特性:E=1 kV/mm,=500 r/minFig 3 Response of the second principal resonance at E=1 kV/mm and =500 r/min

图4 前两阶组合参激共振时的响应特性:E=1 kV/mm,=500 r/minFig 4 Response of the first two combination resonance at E=1 kV/mm and=500 r/min
改变外加电场强度的大小(E=2 kV/mm),得到梁在激励频率时的计算结果如图5所示。由我们前面的研究[6,7]已知,当作用于电流变夹层梁上的外加电场强度增大时,梁的刚度和阻尼损耗因子将增加,梁的运动稳定性增强。故在大的外加电场作用下,受基础激励作用的旋转运动电流变夹层梁也将具有更佳的抗参激共振能力。如当基础激励幅值y0=1.0时,系统在E=1 kV/mm条件下是不稳定的(图2d),但当电场强度增大到E=2 kV/mm时,系统过渡到了稳定状态(图5b)。说明增大电流变夹层结构上的外加电场,能提高系统出现运动不稳定的临界激励幅值,增强结构的稳定性。
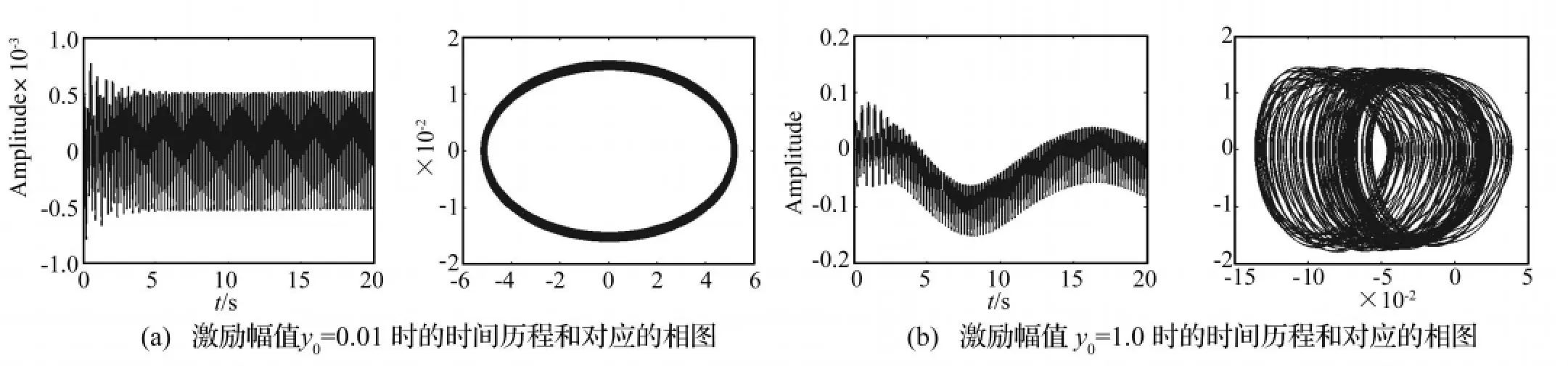
图5 第一阶主参激共振时的响应特性:E=2 kV/mm,=500 r/minFig 5 Response of the first principal resonance at E=2 kV/mm and=500 r/min
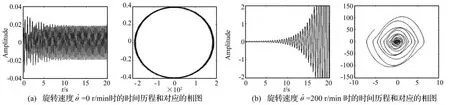
图6 旋转速度对第一阶主参激共振响应的影响:y0=1.5,E=1 kV/mmFig.6 Effect of rotating speed on response of the first principal resonance at y0=1.5 and E=1 kV/mm
图6为旋转速度对系统振动响应特性的影响,其中外加电场强度E=1 kV/mm,基础激励幅值y0=1.1,激励频率=ω1+。图6(a)、图6(b)分别为旋转速度=0和=200 r/min时的振动响应时间历程曲线和对应的相图。由图可见,在旋转速度=0时,系统是作有限周期运动的;而在=200 r/min时,振幅随时间无限增大,系统是不稳定的。故转动速度的提高会加大系统的振动幅度,降低系统的参激振动稳定性。
4 结论
本文对旋转运动电流变夹层梁在基础激励作用下的动力学特性和参激振动稳定性进行了研究。采用一次近似展开方法分析了受基础激励作用的定轴转动电流变夹层梁可能发生参激振动失稳的条件。通过对电场作用下匀转速电流变夹层梁在不同激励参数、控制电场和旋转速度时的振动响应时间历程曲线和对应相图的数值分析,探讨了电场作用下电流变夹层梁受基础激励与定轴转动联合作用时的振动响应特性和稳定性。分析结果表明,在一定的条件下,可以通过控制作用于电流变夹层梁的电场强度来改变系统出现运动不稳定的临界激励幅值,提高结构的动力稳定性。
[1]Gandhi M V,Thompson B S,Choi S B.A new generation of ultra-intelligent composite materials incorporating electrorheological fluids[J].Journal of composite materials,1989,23:1232-1255.
[2]Yalcintas M,Coulter J P.Electrorheological material based adaptive beams subjected to various boundary conditions[J].Journal of Intelligent Material Systems and Structures,1995,6(5):700-717.
[3]Rahn C D,JoshiS. Modeling and controlofan electrorheological sandwich beam[J].Journal of Vibration and Acoustics,Transactions of the ASME,1998,120(1):221-227.
[4]Young K K,Kim J,Choi S-B.Passive and active damping characteristics of smart electro-rheological composite beams[J].Smart Materials and Structures,2001,10(4):724 -729.
[5]任建亭,闫云聚,姜节胜.电流变夹层梁的动力学分析[J].复合材料学报,2002,19(3):114-119.
[6]魏克湘,孟 光,鲁宏权.旋转电流变复合梁的有限元建模分析[J].振动与冲击,2005,24(5):1-3.
[7]Wei K X,Meng G,Zhou S.Vibration control of variable speed/acceleration rotating beams using smart materials[J].Journal of Sound and Vibration,2006,298(4 - 5):1150-1158.
[8]魏克湘,孟 光.周期变速旋转运动电流变夹层梁的参激振动[J].力学学报,2008,40(2):273-280.
[9]吴 涛,冯志华,胡海岩.定轴转动与基础激励下梁的非线性动力学[J].振动工程学报,2003,16(1):11-16.
[10]魏克湘.大范围运动电流变夹层梁的动力学特性与振动控制[D].上海:上海交通大学,2006.
[11]Abbas B A H.Dynamic stability of a rotating timoshenko beam with a flexible root[J]. Journal of Sound andVibration,1986,108(1):25-32.
[12]Tan T H,Lee H P,Leng G S B.Dynamic stability of a radially rotating beam subjected to base excitation[J].Computer Methods in Applied Mechanics and Engineering,1997,146(3-4):265-279.
[13]盛国刚,彭 献,赵 冰.变速旋转梁的建模与运动稳定性分析[J].湖南大学学报,2003,30(2):16-19.
[14]Hamdan M N,El-Sinawi A H.On the non-linear vibrations of an inextensible rotating arm with setting angle and flexible hub[J].Journal of Sound and Vibration,2005,281(1 -2):375-398.
[15]胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000.
[16]Lin C Y,Chen L W.Dynamic stability of a rotating beam with a constrained damping layer[J].Journal of Sound and Vibration,2003,267(2):209-225.

