一种暂态功角稳定故障损失估计方法

刘 哲，贾宏杰

(天津大学智能电网教育部重点实验室，天津 300072)

一种暂态功角稳定故障损失估计方法

刘 哲，贾宏杰

(天津大学智能电网教育部重点实验室，天津 300072)

在进行电力系统暂态稳定风险评估时，科学估算故障引起的系统损失是其核心问题．为此，将故障引起的损失看作将系统从不稳定状态转化为稳定状态所需要的最小控制代价，借助轨迹灵敏度技术，将上述问题转化为一个考虑暂态稳定约束的最优潮流问题实现求解．推导了发电机相对功角同发电机及负荷功率之间的灵敏度系数；利用灵敏度系数和发电机相对功角形成系统的暂态稳定约束，将之引入最优潮流实现对故障最小控制代价的求解；并且利用IEEE-14、New England-39节点等系统验证了所提方法的正确性和有效性．

暂态稳定；风险评估；轨迹灵敏度；最优潮流

随着我国电力系统的发展，联网规模的不断扩大，系统中的不确定性因素不断增加，通过风险分析，合理评估不确定性因素对系统稳定运行的影响意义重大[1]．风险分析的难点是如何准确估算故障引发系统失稳后所造成的损失，利用最优稳定控制代价来近似估计系统损失，为该问题的求解提供了一种可行的途径[1]．文献[2]采取预先设定低压减载策略对系统进行紧急控制，以获得控制代价；文献[3]采取发电机维修、启动和出力调整费用以及负荷紧急控制费用来代替系统失稳造成的损失；文献[4]则利用动态安全域对系统进行预防控制和紧急控制，从而得到系统动态不安全的风险代价．上述方法都需针对故障预设控制策略，在实际应用时会存在一定局限性．

轨迹灵敏度能够在暂态过程中的每一个时刻提供系统丰富的运行信息，且不受元件模型限制[5]，近年来在考虑暂态稳定约束的最优潮流(OPF with transient stability constraints，OTS)[6-7]和暂态稳定控制优化(包括预防控制[8-11]和紧急控制[12])等方面得到成功应用．笔者将故障引起系统失稳后的损失，视为将系统从不稳定状态转化为稳定状态所需最小控制代价，将之转化为一个OTS问题加以求解．故障中的暂态稳定约束通过发电机相对功角加以考虑，后者则利用轨迹灵敏度近似加以估计[13]；发电机出力调整和负荷裁减作为控制手段，不同的控制手段具有不同的控制代价(成本)．当发电机备用容量充足时，优先调整发电机出力(控制成本较低)来维持系统稳定；而当发电机备用容量不足时，则通过控制成本更高的负荷裁减措施来保证系统稳定，其优化过程更贴合实际．

1 轨迹灵敏度

1.1 基本原理

电力系统轨迹灵敏度方法最早由Pai等[5]提出，它认为暂态过程中的系统状态变量同系统参数和状态变量初值近似满足线性关系，而线性系数即为系统的轨迹灵敏度．

电力系统动态可用微分-代数方程表示为

式中：x为系统状态变量；y为系统代数变量；λ为系统控制变量；x0、y0分别表示状态变量和代数变量的初值．将式(1)对λ 求偏导可得

式中：xλ、yλ分别为系统轨迹对控制变量λ的灵敏度矩阵，分别为微分方程组对状态变量、代数变量和控制变量的偏导；分别为代数方程组对状态变量、代数变量和控制变量的偏导数．根据系统初始运行点可求得轨迹灵敏度的初试条件，将式(1)和式(2)联立求解即可得到系统各时刻的轨迹灵敏度．

1.2 发电机功角同其有功出力间的灵敏度

当发电机采取经典模型时，电力系统动态方程为

式中：δi、ωi、Mi、Pg,i、Ei′分别为发电机转子角、转速、转动惯量、机械功率和内电势；Gii、Gij为仅保留发电机内节点后，系统导纳矩阵元素的实部；分别为为系统导纳矩阵元素的虚部；m为发电机节点数．

对式(3)两端分别求发电机k有功出力Pg,k的偏导数可得

由发电机机端功率方程可得

式中：iI˙为发电机注入网络的电流；iS、iα分别为发电机输出的视在功率和功率因数角；Vi、θi分别为发电机机端电压幅值和相角．

发电机内电势iE′˙可表示为

因此，有

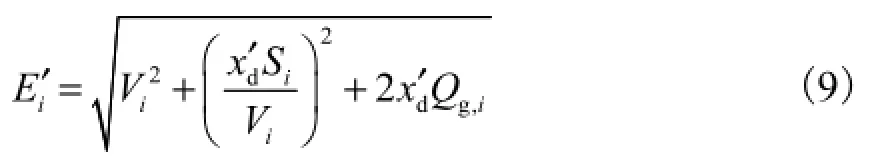
式(9)两端分别对Pg,k求偏导数，得

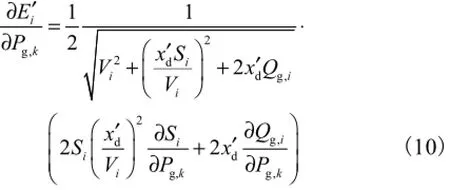
式(7)两端分别对Pg,k求偏导数，得

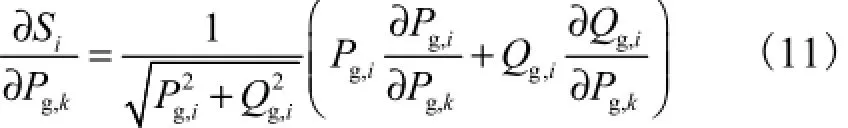
发电机节点无功注入方程为

式中n为系统节点数．

式(12)两端分别对Pg,k求偏导数得

又知稳态时的发电机机械功率为

式(15)两端分别对Pg,k求偏导数，可得

1.3 发电机功角同负荷有功间的灵敏度

假设负荷采取恒阻抗模型，式(3)两端分别对负荷节点k的有功负荷PL,k求偏导数，得

式(18)两端分别对PL,k求偏导数，得

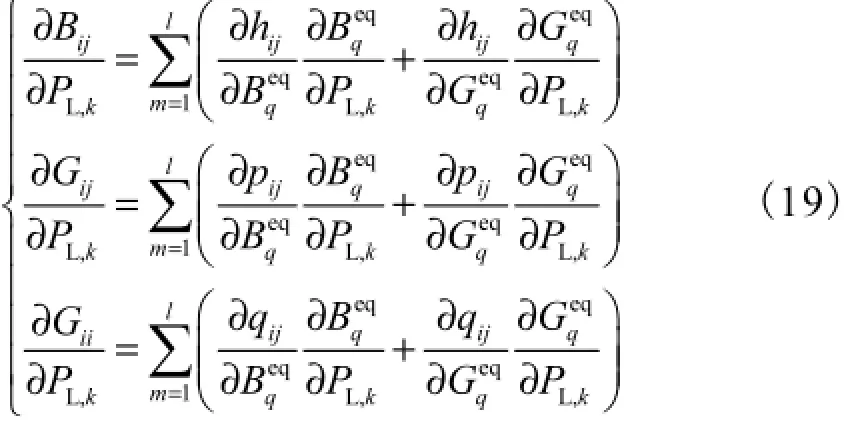
对于恒阻抗负荷而言，等值导纳可表示为

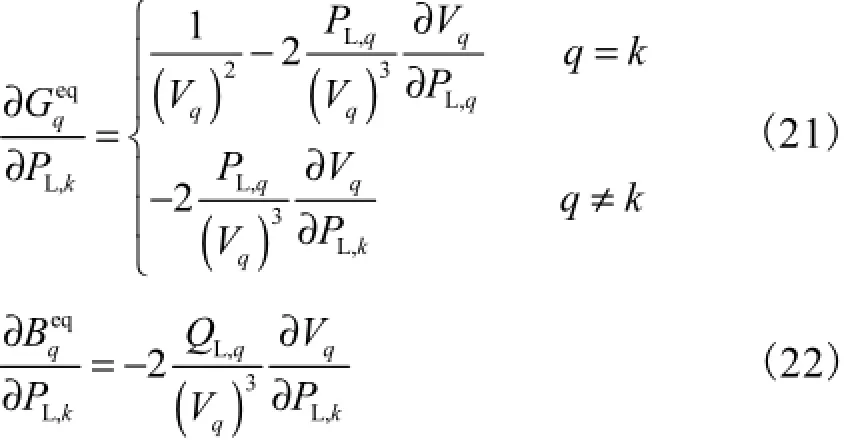
当发电机采用较复杂模型时，依然可以推导出发电机功角同发电机有功出力、负荷有功和无功间的灵敏度关系[14]．但对于复杂模型，为便于计算，可利用数值方法进行轨迹灵敏度的求解[13]．

当系统控制参数发生变化时，利用已求得的发电机绝对功角的轨迹灵敏度，可近似估计发电机ij之间相对功角的变化量，即

2 基于灵敏度的电力系统暂态稳定最小控制成本模型

2.1 暂态稳定最小控制成本模型

将轨迹灵敏度和最优潮流相结合，求解非线性优化问题，即可得暂态稳定最小控制成本，其模型为

约束条件为

上述模型中式(24)表示针对某故障的控制成本，包括上调发电机出力的成本、下调发电机出力成本和裁减负荷成本．为简单起见，本模型将3种控制代价均考虑为控制量的线性函数，进一步亦可采用二次、线性分段成本函数[15]，其求解过程与上述模型类似；式(25)和式(26)分别为有功和无功潮流方程；式(27)为线路潮流约束；式(28)为节点电压约束；式(29)、式(30)和式(31)分别为发电机有功出力上调量约束、下调量约束和无功约束；式(32)表示负荷裁减量约束；式(33)表示暂态功角约束．

为简单起见，对于负荷节点，在进行负荷有功裁减时，负荷无功裁减量计算式为即在控制过程中，负荷功率因数考虑为恒定，若负荷模型为其他形式，将其考虑成最优控制模型的约束条件即可同理求解，式(34)中θ表示负荷的功率因数角向量．

式(24)～式(33)属于典型的含非线性约束最优化模型，求解过程较为简单，求解的流程如图1所示，利为收敛判据，当2个条件同时满足时，表明系统已无可调发电机和负荷，则程序结束．

图1 功角稳定控制流程Fig.1 Flow chart of angle stability control

2.2 优化模型的几点说明

(1) 对于系统中的平衡机，只有在其他发电机和负荷调整不能满足系统潮流平衡时，才参与潮流调整，为达此目的，将平衡机的有功出力调整费用取为普通发电机调整费用的2倍．

(2) 模型中的式(33)为系统的暂态稳定约束，当发电机相对功角超过δlim时即认为系统发生暂态失稳．不妨假设系统中有m个发电机和l个负荷，则有Cm2个发电机相对功角，其中有c个相对功角绝对值大于δlim，进而有

(3) 用图2简单解释式(33)中tsen时刻的选取原则，该图给出了一个3机简单系统的相对功角：2号机和1、3号机的功角相互摆开，图中只画出了δ23和δ13，曲线δ12和δ23非常近似，但不重合．在t＞后，δ12、δ23绝对值将大于δlim，而相对功角δ13的绝对值一直小于δlim．假设在δ12、δ23曲线中，δ12最先达到δsen，此时刻记为，为了保证在时刻之前所有相对功角都位于[−δlim,δlim]内，取tsen=．δsen和δlim是预先设定的一个相对功角的阈值，不同系统阈值的选取可能不同[10]，δlim越小表明稳定区域越小，暂态稳定最优控制成本将越大，考虑到功角稳定问题大多是单摆失稳，因此δsen一般选取在2π到10π之间即可．本文暂不考虑预设阈值对算法的影响，对同一系统δsen和δlim取值相同．

图2 发电机相对功角曲线示意Fig.2 Sketch of relative rotor angle curves

(4) 在式(33)中，有

式中

灵敏度矩阵的构成式为

由于负荷按照恒功率因数进行处理，因此将发电机相对功角同无功负荷的灵敏度按照相应的功率因数折合到有功负荷灵敏度中表示发电机i和j之间的相对功角同负荷q间的灵敏度，且有

式中qθ为负荷q的功率因数角．

3 算例分析

以IEEE-14和New England-39节点系统为例，对本文中方法进行验证，计算中取δlim＝π[10]，ε=0.05MW．对于14节点系统，发电机采用次暂态模型，负荷采取恒阻抗负荷，δsen＝5π；对于39节点系统，发电机采用经典模型，负荷采用恒阻抗模型，δsen＝10π．除平衡节点以外其他发电机控制费用：=10 K/MW，平衡节点的控制费用：=＝20 K/MW，负荷控制费用：CL＝30 K/MW，K为某种货币单位．

3.1 IEEE-14节点系统

假设线路2-4靠近节点2处发生三相短路，临界切除时间tcr＝0.29 s，设此故障由于控制设备原因，其实际切除时间为：tcl＝1.5tcr＝0.435 s，节点电压最大值均取1.15 p.u.，节点电压最小值均取0.85 p.u.，此时系统出现如图3所示的失稳情况．

图3 发电机功角曲线(IEEE-14)Fig.3 Rotor angle curves(IEEE-14)

从图3中可以清晰地看到发电机被分成了{1，2}和{3，4，5}2组．

情景1 当发电机有功备用充足时，不需要调整负荷，只通过调整发电机出力即可实现系统稳定，控制结果如表1所示，最小控制代价为1,225.10,K．调整后各发电机功角曲线如图4所示，从图4可以看出，经过发电机调整系统可保持暂态稳定．

表1 情景1的发电机控制结果(IEEE-14)Tab.1 Results of generator control for scenario 1(IEEE-14)

图4 情景1调整后发电机功角曲线(IEEE-14)Fig.4 Rotor angle curves after control for scenario 1 (IEEE-14)

情景2 当发电机备用不足时，仅靠调整发电机，将不能达到系统稳定的目的，此时还应伴随负荷裁减控制．作为示例，不妨假设G3、G4、G5号发电机有功出力的最大值由原先的100,MW变成20,MW，通过优化计算，发电机和负荷的调整结果如表2和表3所示．此时，发电机和负荷总的控制费用为3,294.67,K，调整后发电机的功角曲线如图5所示，可以看出系统亦能保持稳定，但由于发电机有功储备较小，需要进行负荷裁减，情景2的控制代价要高于情景1．

3.2 New England-39节点系统

假设线路22-21靠近节点22处发生三相短路，临界切除时间tcr＝0.13 s，因某种原因，系统实际故障切除时间变为：tcl＝1.5tcr＝0.2,s，节点电压最大值取1.15 p.u.，节点电压最小值取0.85,p.u.，此时系统出现如图6所示的失稳情况，从图6中可以看出10台发电机被分为{1，3，4，5，8，9}、{2}、{6，7}、{10}4组．

表2 情景2的发电机控制结果(IEEE-14)Tab.2 Results of generator control for scenario 2(IEEE-14)

表3 情景2的负荷控制结果(IEEE-14)Tab.3 Results of load control for scenario 2(IEEE-14)

图5 情景2调整后发电机功角曲线(IEEE-14)Fig.5 Rotor angle curves after control for scenario 2 (IEEE-14)

图6 发电机功角曲线(New England-39)Fig.6 Rotor angle curves(New England-39)

情景1 当发电机备用充足时，发电机调整结果如表4所示．由于发电机均具有充足的有功调解备用，因此故障后，通过调整发电机出力即可保证系统恢复稳定运行，系统最小控制成本为9,564.39,K，控制后系统功角曲线如图7所示．

情景2 假设10号发电机有功出力最大值由1,600,MW变为1,400,MW，系统将没有足够的发电机备用容量可调，因此同样的故障出现后，单纯依靠发电机调整无法保证系统稳定，必须辅以负荷裁减，此时系统的控制方案和最小控制成本示于表5和表6．不难看出，由于发电机缺乏足够的有功备用，系统的故障控制成本升高变为11,128.62,K，控制后的系统功角曲线示于图8．

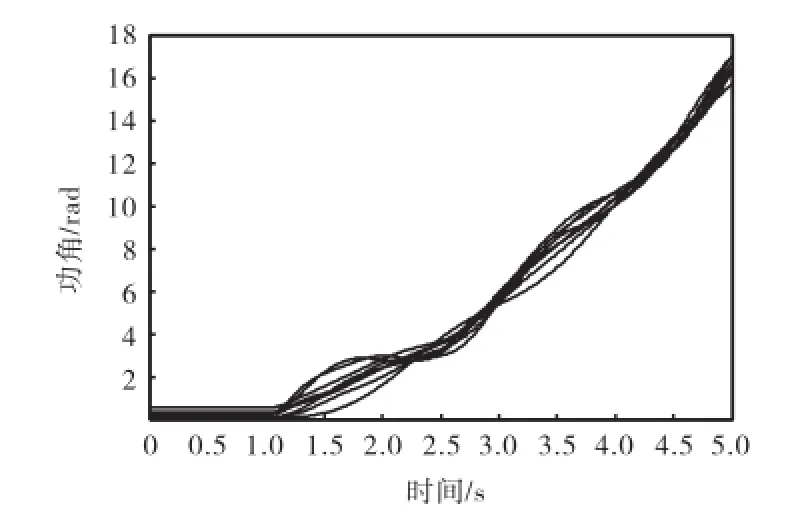
图7 情景1调整后的发电机功角曲线(New England-39)Fig.7 Rotor angle curves after control for scenario 1 (New England-39)

表4 情景1的发电机控制结果(New England-39)Tab.4 Results of generator control for scenario 1(New England-39)

表5 情景2发电机控制结果(New England-39)Tab.5 Results of generator control for scenario 2(New England-39)

表6 情景2负荷控制结果(New England-39)Tab.6 Results of load control for scenario 2(New England-39)

图8 情景2调整后发电机功角曲线(New England-39)Fig.8 Rotor angle curves after control for scenario 2 (New England-39)

4 结 语

本文中提出了一种基于轨迹灵敏度的暂态功角稳定故障损失估计方法，将故障损失用将系统从不稳定状态转化为稳定状态所需要最小控制代价加以考虑．利用轨迹灵敏度技术近似估计系统参数变化后发电机相对功角的变化量，进而将暂态稳定约束引入最优潮流模型，以发电机调整和负荷裁减作为控制手段，实现最小控制代价的求解．本文尚未考虑故障随机性的影响，但经过大量算例验证(包括不同的故障线路、不同的故障类型和切除时间等)，算法对所有故障具有普遍适用性，这为进一步开展电力系统暂态风险评估研究奠定了基础．

［1］ 薛禹胜，刘 强，董朝阳，等. 关于暂态稳定不确定性分析的评述[J]. 电力系统自动化，2007，31(14)：1-6.

Xue Yusheng，Liu Qiang，Dong Zhaoyang，et al. A review of non-deterministic analysis for power system transient stability[J]. Automation of Electric Power Systems，2007，31(14)：1-6(in Chinese).

［2］ 赵珊珊，仲悟之，张东霞，等. 暂态电压稳定风险评估方法及应用[J]. 电力系统自动化，2009，33(19)：1-4.

Zhao Shanshan，Zhong Wuzhi，Zhang Dongxia，et al. A transient voltage instability risk assessment method and its application[J]. Automation of Electric Power Systems，2009，33(19)：1-4(in Chinese).

［3］ Vittal V，McCalley J D，Van Acker V，et al. Transient instability risk assessment[C]//Proceedings of Power Engineering Society Summer Meeting. Edmonton，Canada，1999：206-211.

［4］ 余贻鑫，王东涛. 输电系统动态安全风险评估与优化[J]. 中国科学 E辑：技术科学，2009，39(2)：286-292.

Yu Yixin，Wang Dongtao. Dynamic security risk assessment and optimization of power transmission system[J]. Science in China Series E：Technological Sci-ences，2009，39(2)：286-292(in Chinese).

［5］ Hiskens I A，Pai M A，Trajectory sensitivity analysis of hybrid systems[J]. IEEE Transactions on Circuits and Systems，2000，47(2)：204-220.

［6］ 孙景强，房大中，锤德成. 暂态稳定约束下的最优潮流[J]. 中国电机工程学报，2005，25(12)：12-17.

Sun Jingqiang，Fang Dazhong，Chui Decheng. Optimal power flow with transient stability constraints [J]. Proceedings of the CSEE，2005，25(12)：12-17(in Chinese).

［7］ 李传栋，杨金刚，陈家荣. 暂态稳定约束下的最优潮流[J]. 电力系统及其自动化学报，2009，21(6)：45-50.

Li Chuandong，Yang Jingang，Chen Jiarong. Optimal power flow with transient stability constraints[J]. Proceedings of the CSU-EPSA，2009，21(6)：45-50(in Chinese).

［8］ Nguyen T B，Pai M A. Dynamic security-constrained rescheduling of power systems using trajectory sensitivities[J]. IEEE Transactions on Power Systems，2003，18(2)：848-854.

［9］ 孙景强，房大中，周保容. 基于轨迹灵敏度的电力系统动态安全预防控制算法研究[J]. 电网技术，2004，28(21)：26-30.

Sun Jingqiang，Fang Dazhong，Zhou Baorong. Study on preventive control algorithm for dynamic security of power systems based on trajectory sensitivity method[J]. Power System Technology，2004，28(21)：26-30(in Chinese).

［10］ Fang Dazhong，Yang Xiaodong，Sun Jingqiang，et al. An optimal generation rescheduling approach for transient stability enhancement[J]. IEEE Transactions on Power Systems，2007，22(1)：386-394.

［11］ 周鲲鹏，陈允平. 运用轨迹灵敏度的电力系统动态安全控制[J]. 电网技术，2003，27(12)：46-50.

Zhou Kunpeng，Chen Yunping. Power system dynamic security control based on trajectory sensitivity[J]. Power System Technology，2003，27(12)：46-50(in Chinese).

［12］ Zima M，Andersson G. Stability assessment and emergency control method using trajectory sensitivities[C]//Proceedings of IEEE Bologna Power Tech Conference. Italy，2003：189-194.

［13］ Nguyen T T，Karimishad A. Fast and accurate method for dynamic security-constrained economic dispatch via sensitivity analysis[C]// Proceedings of IEEE Power Engineer-ing Society General Meeting． Tampa，FL，USA，2007：1-8.

［14］ Nguyen T B，Pai M A，Hiskens I A. Direct computation of critical clearing time using trajectory sensitivities[C]//Proc of IEEE Power Engineering Society Summer Meeting. Seattle，WA，USA，2000：604-608.

［15］ Wang Hongye，Murillo-Sanchez C E，Zimmeraman R D，et al. On computational issues of market-based optimal power flow[J]. IEEE Transactions on Power Systems，2007，22(3)：1185-1193.

An Evaluation Method for Transient Stability Contingency Cost

LIU Zhe，JIA Hong-jie
(Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China)

In power system transient stability risk assessment，it is a core issue to properly estimate the cost consequences caused by instability events. In this paper，the cost consequences of a contingency are considered as the minimum control cost to move the system from instability to stability under the contingency. Trajectory sensitivity is employed to properly consider the transient stability constraints in the optimal power flow(OPF).The minimum objective of the OPF is the determination of contingency cost. The sensitivities of the relative rotor angle with respect to the output of generator and the dispatchable load are firstly derived. The information is then used to imitate the transient stability constraints in the OPF. The correctness and effectiveness of the proposed method in this paper is finally validated by some systems，such as IEEE 14-bus system and New England 39-bus system.

transient stability；risk assessment；trajectory sensitivity；optimal power flow

TM712

A

0493-2137(2011)09-0759-09

2010-09-20；

2010-11-18．

国家重点基础研究发展计划(973计划)资助项目(2009CB219701，2010CB234600)；天津市科技发展计划资助项目(09JCZDJC 25000)；“十一五”国家科技支撑计划重大资助项目(2006BAJ03A06)；博士学科点专项科研基金资助项目.

刘 哲（1985— ），男，博士研究生，liuzhe@tju.edu.cn.

贾宏杰，hjjia@tju.edu.cn.