灰色模型在沉降监测数据处理中的应用

刘玉财，何涛，李胜友，王洋

(天津市测绘院，天津 300191)

1 概述

在大型工程施工及运营管理过程中，在建工程自身及其对临近建筑物的变形监测工作显得尤为重要。变形监测是通过对设置在建筑物上的观测点进行周期性重复观测以获取对象的变形信息。对变形信息的处理主要包括获取真实的变形值并进行解释以及对未来变形量做出准确可靠的预报。对于周期性的变形监测，对其预测方法研究较多，常用的统计学分析方法主要包括:回归分析法，时间序列法、灰色模型等。其中灰色模型预测不需要大量的实测数据，且变形数据既可以是线性的也可以是非线性的，可以随时对模型进行修正以提高其预测精度，具有较高的实用性。本文首先讨论了灰色模型的基本建模流程，并结合某基坑开挖工程中对周围建筑物的变形监测数据为例，讨论了传统的GM(1，1)灰色模型和非等步长GM(1，1)灰色模型的预测效果，以期建立有效的变形预报模型，为建筑的设计、施工、管理和科学研究提供可靠的资料［8，9］。

2 灰色模型GM(1，1)的建立

灰色系统理论研究的是贫信息建模，其核心是灰色动态模型，特点是生成函数和灰色微分方程。灰色动态模型是以灰色生成函数概念为基础，以微分拟合为核心的建模方法，灰色系统理论认为:一切随机量都是在一定范围内、一定时段上变化的灰色量和灰过程，对灰色量的处理不是寻求它的统计规律和概率分布，而是将杂乱无章的原始数据列，通过一定的方法处理，变成比较有规律的时间序列数据，即按照以数找数的思想，再建立动态模型［1，2］。

2.1 灰色模型的建模原理

灰色模型一般建模原理是通过对非负离散原始序列X(0)进行一次累加生成(1-AGO)获得一个新的生成序列X(1)后，对生成序列建立一阶微分方程为:

式中:

把求取的参数带入(1)式，求出离散解即时间响应函数为:

对^x(1)(k+1)做累减生成可得还原数据:

其中，-a称为发展系数，u称为灰色作用量。当k〈n时，称 ^x(0)(k)为模型模拟值;当k=n时，称^x(0)(k)为模型滤波值;当k〈n时，(k)为模型预测值。

2.2 传统GM(1，1)模型

当观测资料为非等间隔序列时，应先将非等间隔序列的原始观测资料变成等间隔序列，再以此为基础生成预测模型，非等间隔灰色模型有内插值改进法、二次参数拟合法、直接累加生成法、单位时段差系数修正法等生成非等间隔 GM 模型［2，3］。

当采用单位时段差系数修正法时，对于非等间隔序列观测数据，数据序列值对应的观测时段为:

则各时段与平均时段的单位时段差系数u(ti)为:

则各时段总的差值为:

可等间隔点的灰指数为:

即可得到等间隔序列，利用前述的一般灰色建模方法对非等间隔序列改化后的等间隔序列建立非等间隔的t时刻的灰色GM(1，1)模型为:

2.3 非等步长GM(1，1)模型

传统模型的建立是非等间隔观测数据列改化为等间隔数据列后按一般灰色模型建模方法进行模型建立，针对数据非等间隔特点，以相邻观测时间间隔为权，做观测序列的1-WAGO生成，可以直接建立非等步长 GM(1，1)模型［4］。

设ti时刻观测数据为x(0)ti，当相邻观测时间间隔不等时，对x(0)ti做一次1-WAGO生成序列为:

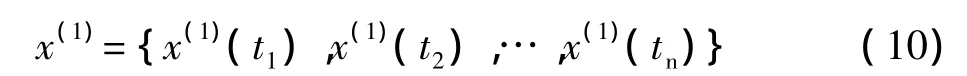
x(1)的GM(1，1)的白化微分方程式为:

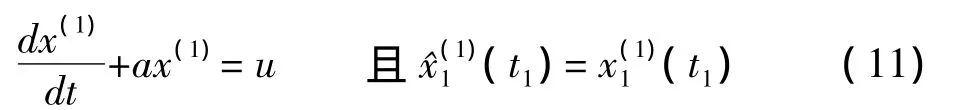
式中a，u为参数，求得微分方程的解，并求其差分还原公式，则可得到非等步长GM(1，1)模型预测方程:

以上即为一元一阶灰色模型GM(1，1)不同数据观测序列采用的模型。

2.4 模型的精度评定

对模型精度的评定方法有残差大小检验、关联度检验和后检差检验三种，灰色模型的精度通常用后验差方法检验［5，7］。

设有GM(1，1)模型得到:

计算残差为:

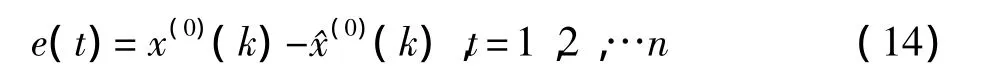
记原始序列x(0)及残差数列e的方差分别为则有:

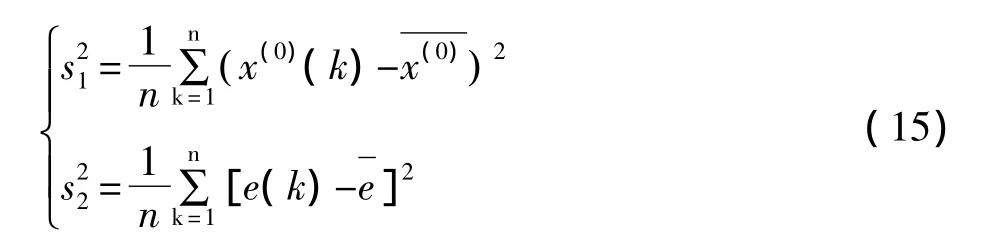
则后验差比值C、小误差概率p为:

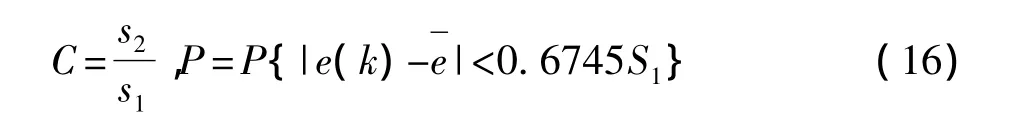
模型精度等级判断式为:模型精度等级=max{P所在的级别，C所在的级别}，P，C的精度判别等级如表1所示。

模型精度等级参照表 表1

3 实例分析

利用实际建筑物某单位沉降监测点的数据进行建模预测，采用第J18的观测数据为例，选取前10期的数据进行灰色模型建模，在建模之前对原始观测数据进行处理，使之满足灰色建模需要数据的非负性，处理的方法常采用累积变化量的绝对值加上初始观测的高程值得到非负数据序列。建模的初始数据如表2所示。

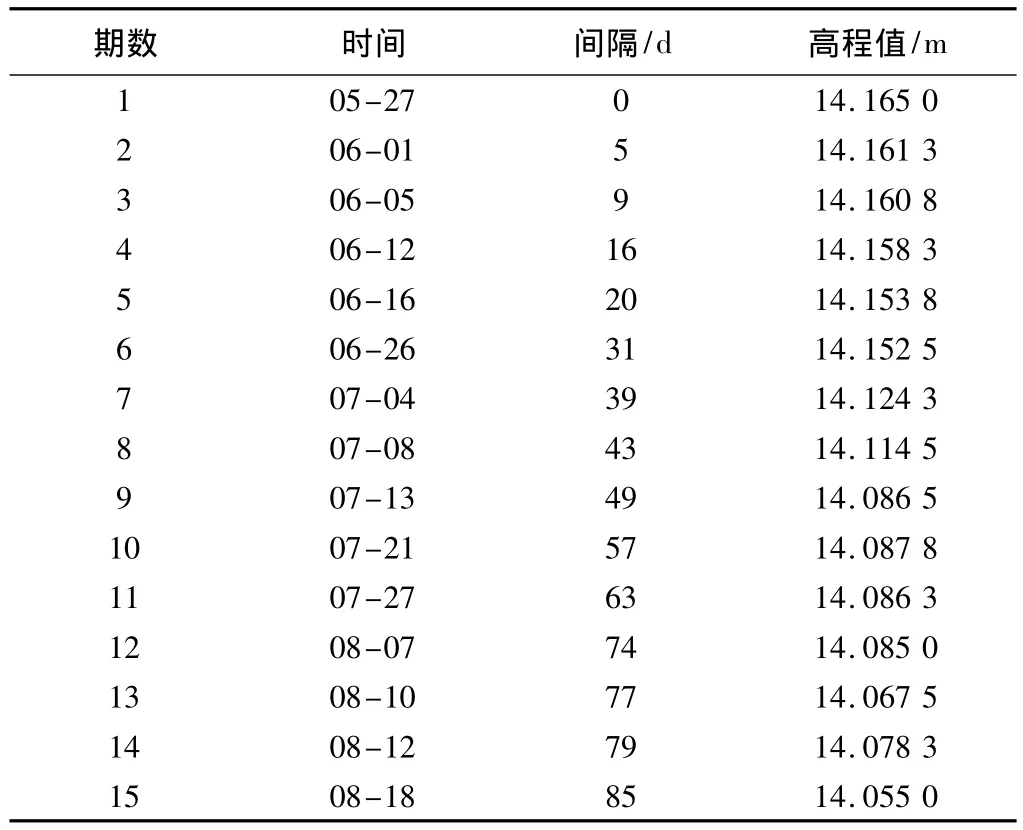
沉降监测数据 表2

3.1 传统GM(1，1)建模

根据前面介绍的非等间隔数据建模方法，利用前10期的数据分别以传统的GM(1，1)和对观测序列做1-WAGO生成直接建立非等步长GM(1，1)模型方法建模。

传统GM(1，1)建模:根据表2数据J18在各个观测时段的高程值，选择前10期数据，依据2.2所述建模方法建立灰色模型，根据式(5)～式(8)建立非等间隔观测数据的等间隔数据序列，利用式(2)计算得到建立GM(1，1)所需白化值参数:

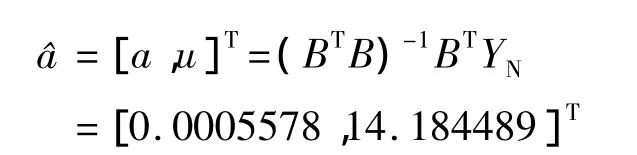
由求得的白化值根据(1)式可以建立灰色微分方程的时间响应函数:

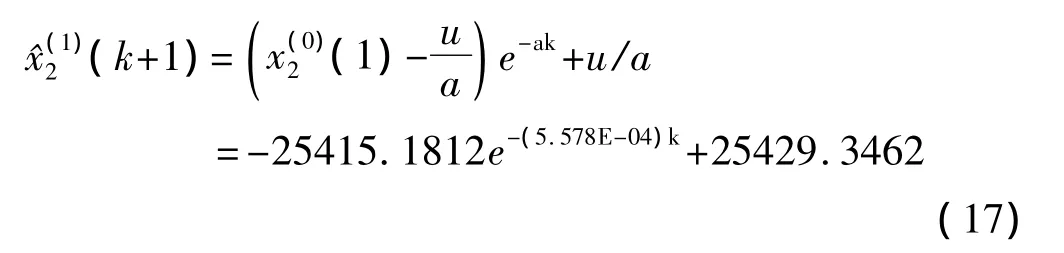
还原为非等间隔数列中与时间t有关的响应函数为:

3.2 非等步长模型建模

对观测序列按照式(10)以相邻观测时间间隔为权进行1-WAGO生成，直接生成非等步长GM(1，1)模型。根据(11)式求得原始观测序列的1-WAGO生成序列的白化微分方程后利用式(2)计算得到建立非等步长GM(1，1)所需白化值参数a，u的最小二乘解为:

根据(12)式建立预测方程为:

表3为传统模型和非等步长GM(1，1)模型的对前10期的拟合结果及对后5次的预测结果。

传统模型和非等步长GM(1，1)模型的对前10期的拟合结果及对后5次的预测结果 表3

数据处理的分析:

(1)从表3中可以看出，传统模型拟合平均误差为0.572 4 mm，后验差比值为C=0.459 5，非等步长模型拟合平均误差为 0.547 7 mm，后验差比值为C=0.427 8，说明两种模型的拟合精度和可靠性具有一定差别但差别不是很大。

(2)从表中可以知道传统模型预测中误差为11.36 mm，而非等步长预测中误差为 9.68 mm，说明两种模型都可以用于短期的预测，但非等步长模型有更高的预测精度。

(3)分析表3中数据，传统模型和非等步长模型的检验参数均小于0.35，中误差概率P均大于0.95说明模型精度均达到Ⅰ精度，都能取得较好的拟合精度和预测结果。比较两种模型的平均误差、方差检验参数发现非等步长具有相对较高的预测精度、较小的残差离散度和较好的外推性，可以看出两模型对沉降趋势均可较准确预测，非等步长模型精度较优。

4 结语

(1)采用灰色建模对建筑物的沉降预测能够达到较好的预测结果，对工程的实施具有一定的借鉴作用，但建筑物沉降的不均匀会导致观测值出现偶然反弹，形成随机振荡序列，这种振荡对模型预测精度有很大影响。本文中利用非等步长灰色GM(1，1)模型，对建筑物沉降进行了预测和分析，验证了该方法的有效性，但并未表现出比传统模型更高的灵敏性，因此由于沉降机理的不确定性，灰色模型的选择应根据工程的实际情况进行数据分析与处理。

(2)每种数学模型都有其局限性，由于建筑施工是一个动态的过程，建筑物的沉降将不断受到系统内外多方面因素的综合作用，远期观测数据所反映建筑物沉降变化的真实程度随时间的推移逐步降低，并且灰色模型本身随着预测时间的变长，预测精度也会降低，这就需要在实践中对模型不断试验，探索模型对数据序列的要求，以求在尽量减少运算的基础上达到精度要求，从而提高模型的预测精度。

(3)GM(1，1)模型要求监测数据为等间隔的数据序列，但实际工作中由于客观原因，所得到的原始数据序列往往是非等间隔的，因此需要对数据序列进行数学变换成等间隔的数据，但非等步长GM(1，1)模型则可以直接进行建模，减少了数据计算量，且其预测与拟合精度并没有降低，显示了其实用价值。

［1］邓聚龙.灰色预测与决策［M］.武汉:华中科技大学出版社，2002

［2］李斌，朱健.非等间隔灰色GM(1，1)模型在沉降数据分析中的应用［J］.测绘科学，2007，32(4):52-55

［3］潘华志，卫建东，夏治国等.动态灰色模型在变形监测中的应用［J］. 测绘科学，2007，32(4):121-123

［4］刘明波，田林亚，孙和平.非等步长GM(1，1)模型及其在大堤沉降监测中的应用［J］.测绘工程，2006，15(03):58-60

［5］肖文，范志平，蔡仁澜等.灰色系统GM(1，1)模型在建筑物变形监测中的应用［J］.地理空间信息，2010，8(2):44-46

［6］张清华，隋立芬，牟忠凯等.利用改进灰色模型的钟差预报算法及其精度分析［J］.测绘科学，2012-01

［7］王明礼.三种灰色系统模型的预测比较［J］.统计与决策，2011，8(332):35-37

［8］刘思峰，邓聚龙.GM(1，1)模型的适用范围［J］.系统工程理论与实践，2000，5:121-124

［9］吴江淮.建筑物静态变形监测数据分析与处理［D］.同济大学，2007