基于四阶累积量的共形阵列波达方向估计算法
齐子森 郭 英 王布宏 王永良
(1.空军工程大学电讯工程学院,陕西 西安 710077;2.空军雷达学院兵器运用工程军队重点实验室,湖北 武汉 430019)
1.引 言
共形阵列天线的诸多优点[1]使其成为航空、航天和临近空间探测成像系统中天线分系统发展的重要趋势。共形阵列天线的空间谱估计技术是共形阵列天线信号处理理论体系的重要组成部分,对共形阵列天线高分辨波达方向(DOA)估计方法的研究具有重要的意义。由于共形载体曲率的影响,共形阵列天线中各天线单元方向图的法线指向不一致,即使天线单元极化纯度很高(没有交叉极化),由于单元指向的差异,整个阵列将存在严重的交叉极化效应,这就导致了共形阵列天线的信源方位估计需要与信源的极化状态联合进行。多极化特性(Polarization Diversity)是共形天线阵列流形的最大特点,在考虑共形阵列天线DOA估计问题时,信源方位参数与信源极化参数的“耦合”使得许多适用于经典阵列(如线阵、面阵等)的DOA估计方法均无法简单地移植应用到共形阵列天线中。
对共形阵列天线DOA估计技术的已有研究主要集中在简化模型条件下的DOA估计算法研究[2-6]、共形天线阵列流形的极化建模[7-8],信源极化状态先验已知条件下不同阵列形式DOA估计算法的性能分析与比较[9]以及针对锥面共形载体的盲极化DOA估计方法[10]。充分考虑共形天线多极化特点,适用于多种共形载体的DOA估计方法还未见报道。本文针对共形阵列天线的DOA估计特点,在阵列接收信号为窄带远场非高斯独立入射信号叠加高斯噪声的前提下,通过合理的阵元排列方式,利用四阶累积量对阵列孔径的扩展性,结合旋转不变子空间(ESPRIT)算法[11],提出了一种共形阵列天线盲极化DOA估计算法。该算法在入射信号极化参数未知条件下实现了多种几何结构的共形阵列天线高分辨DOA估计,具有一定的普适性。 以柱面共形阵列天线DOA估计为例,详细推导了算法机理,给出了算法步骤。最后通过Monte Carlo仿真实验验证了所提算法的有效性。
2.共形阵列天线窄带数据模型
准确建立阵列接收数据的数学模型是进行DOA估计的前提,导向矢量是阵列天线对单位强度入射信号空间响应的本质体现,也是获得阵列快拍数据模型的基础,共形阵列天线的数据模型与经典阵列天线数据模型的不同完全由导向矢量的差异所决定。阵元个数为m的经典阵列天线的导向矢量模型为
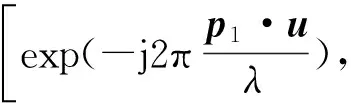
(1)
式中:Pi为第i个阵元在全局坐标系中的位置矢量;u为窄带远场入射信号的方向矢量;λ为入射信号波长。而在共形阵列天线中,由于共形载体曲率的影响,使得处于不同空间位置阵元的方向图具有了不同的指向,所以共形阵列天线导向矢量的建模必须考虑各阵元方向图的影响,此特点直接导致了共形天线阵列流形的多极化特性。文献[7]-[9]通过完成单元方向图的旋转变换,给出了共形阵列天线导向矢量建模的统一方法,在此基础上可获得共形阵列天线对窄带、远场入射信号的响应模型如下
(2)
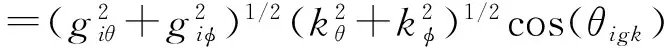
=|gi‖pl|cos(θigk)
=gi·pl
=giθkθ+giφkφ
(3)
kθ,kφ分别为入射信号极化矢量在极化基矢量uθ,uφ上的分量,uθ和uφ为正交单位矢量;gi为单元方向图;pl为信号电场方向矢量;giθ,giφ分别表示第i个阵元单元方向图在uθ,uφ上的分量;θigk表示矢量gi与矢量pl的夹角。当信源个数为n时,共形阵列天线的快拍数据模型为[9-10]
X=AS+N=(AθKθ+AφKφ)S+N
(4)
S=[s1,s2,…,sn]T
(5)
N=[n1,n2,…,nn]T
(6)
Aθ=[aθ(θ1,φ1),aθ(θ2,φ2),…,aθ(θn,φn)]
(7)
Aφ=[aφ(θ1,φ1),aφ(θ2,φ2),…,aφ(θn,φn)]
(8)
Kθ=diag(k1θ,k2θ,…,knθ)
(9)
Kφ=diag(k1φ,k2φ,…,knφ)
(10)
式中:A为流形矩阵;S为信号矢量;N为噪声矢量;n为信源个数;K=diag(k1,k2,…,kn)表示矩阵K为以k1,k2,…,kn为主对角线元素构成的对角阵;θi,φi表示第i个入射信号在全局坐标系中的俯仰角与方位角;kiθ,kiφ分别为第i个入射信号极化矢量在uθ,uφ上的分量。
综合上述分析可知:共形阵列天线快拍数据模型中含有信源方位参数与入射信号的极化参数,这不同于以往经典阵列天线的快拍数据模型。所以,共形阵列天线DOA估计具有其特殊性:
1) 向矢量建模需考虑单元天线方向图的影响,使得共形天线阵列流形具有多极化特点;
2) 阵列接收数据由信源方位参数(俯仰角参数和方位角参数)与入射信号极化参数联合决定;
3) 进行DOA估计时,通常需要DOA与信源极化状态去耦(或联合)估计。
针对共形阵列天线DOA估计的上述特点,在信号矢量S服从非高斯独立分布,噪声矢量N服从高斯分布的前提下,本文利用四阶累积量的阵列扩展特性,结合ESPRIT算法,实现了共形阵列天线DOA与信源极化状态的去耦估计。
3.四阶累积量的阵列扩展
利用ESPRIT算法进行DOA估计的前提条件是构建完全相同的成对子阵,且子阵对之间相应阵元的距离矢量相同,应用ESPRIT算法进行DOA估计时,仅利用了子阵对间距离矢量引起的采样相差,而对子阵导向矢量的具体形式不敏感。若在共形阵列天线中可以构建出ESPRIT算法所需要的子阵对,且成对子阵间的距离矢量与天线单元方向图无关,那么即可实现DOA与信源极化状态的去耦,完成共形阵列天线的盲极化DOA估计。但是共形载体几何结构的任意性给构建ESPRIT算法的子阵对带来了巨大的难度,文献[12]指出实际阵元(实际存在的阵元)接收数据的四阶累积量运算可等效于实际阵元与在某些特殊位置虚拟的阵元(实际不存在的阵元)之间以及虚拟的阵元之间接收数据的相关运算,即通过四阶累积量可获得阵列扩展后的数据协方差矩阵,从而实现阵列口径的扩展。虚拟阵元的出现为在共形阵列天线中构建ESPRIT算法的子阵对提供了方便,使共形阵列天线的盲极化DOA估计成为可能。
由于零均值高斯分布平稳过程的四阶累积量为零,所以当阵列接收数据是服从非高斯独立分布的入射信号叠加高斯噪声时,四阶累积量在阵列天线DOA估计中具有广泛的应用,其阵列扩展性和抑制加性高斯噪声的特性给DOA估计带来了极大的方便。快拍数据协方差矩阵是由各阵元接收数据的相关运算获得,在不考虑噪声协方差矩阵的前提下,快拍数据的相关运算可以理解为阵元空间位置矢量的求和运算,接收数据的四阶累积量变换亦可以理解为阵元空间位置矢量的求和运算,但四阶累积量运算可实现实际阵元与虚拟阵元间采样数据的相关运算,以及虚拟阵元间采样数据的相关运算,即可实现阵列口径的扩展[12]。所以对阵列实际阵元接收数据进行四阶累积量变换,可以得到虚拟阵元与实际阵元以及虚拟阵元之间的相关数据,从而获得阵列扩展后的协方差矩阵,扩展后的导向矢量由实际阵元与虚拟阵元共同决定,等同于增加了阵元个数,所以四阶累积量的阵列扩展性可完全反映在导向矢量上[12]。其具体细节如下:
阵元个数为m,单元方向图为gi的阵列,当波束矢量为u时,其导向矢量为
a(θ,φ) =[r1exp(-jk0p1·u),…,
rmexp(-jk0pm·u)]
(11)
式中:Pi为第i个阵元在全局坐标系中的位置矢量;k0=2π/λ.经四阶累积量阵列口径扩展后的阵列导向矢量为原导向矢量(如式(11)所示)与其本身共轭的Kronecker积
b(θ,φ)=a(θ,φ)⊗a*(θ,φ)
=[r1exp(-jk0p1·u),…,
rmexp(-jk0pm·u)]⊗
[r1exp(jk0p1·u),…,
rmexp(jk0pm·u)]
r1rmexp{-jk0(p1-pm)·u},
r2r1exp{-jk0(p2-p1)·u},
⋮
rmr1exp{-jk0(pm-p1)·u},…,
rmrm-1exp{-jk0(pm-
(12)
当快拍数据为非高斯独立窄带信号叠加高斯噪声时,四阶累积量可以将噪声抑制,所以考虑加性高斯噪声时上述分析亦适合。对实际阵元接收数据进行四阶累积量变换可得扩展后的数据协方差矩阵[13]
Rcum4((k1-1)2m+k3,(k2-1)2m+k4)
=B(θ,φ)C4BH(θ,φ)
(13)
B(θ,φ)=[A(θ,φ)⊗AH(θ,φ)]
=[a(θ1,φ1)⊗aH(θ1,φ1),a(θ1,φ1)⊗aH(θ2,φ2),
…,a(θ1,φ1)⊗aH(θn,φn),
a(θ2,φ2)⊗aH(θ1,φ1),a(θ2,φ2)⊗aH(θ2,φ2),
…,a(θ2,φ2)⊗aH(θn,φn),
⋮
a(θn,φn)⊗aH(θ1,φ1),a(θn,φn)⊗aH(θ2,φ2),
…,a(θn,φn)⊗aH(θn,φn)]
(14)
C4((l1-1)n+l3,(l2-1)n+l4)
(15)
式中:Rcum4(i,j)表示矩阵Rcum4的第i行,第j列元素;C4(i,j)表示矩阵C4的第i行,第j列元素; ⊗表示Kronecker积;ki表示第ki个阵元,且ki∈(1,2,…,2m);li表示第li个入射信号,且li∈(1,2,…,2n); 因为入射信号为零均值的非高斯信号,所以C4中仅有n个非零元素,即l1=l2=l3=l4时获得,且非零元素对应与式(14)中的a(θi,φi)⊗aH(θi,φi)相乘。
综上分析可知:通过在式(12)所示导向矢量中选择阵元即可构建ESPRIT算法所需要的子阵对,且子阵对间的距离矢量与单元方向图无关,从而可实现共形阵列天线的盲极化DOA估计。
4.算法设计
4.1 共形载体上的阵元设置
ESPRIT算法是利用信号子空间的旋转不变性进行参数估计的子空间类算法,此方法假设存在两个完全相同的子阵,且两子阵的距离d(即子阵对中对应阵元的距离,一般选为λ/2)已知,以d对每个入射信号ui引起的空间采样相差exp(-jk0d·ui)为主对角元素可构成两子阵流形矩阵的旋转矩阵φ,通过特征值分解可从两子阵接收数据中获得张成同一信号子空间的矩阵US1,US2,进而可求得US1,US2的旋转矩阵ψ,利用φ与ψ的相似性进行DOA估计。ESPRIT算法每估计一个参数就需要一对结构完全相同且具有一定距离的子阵对,所以应用ESPRIT算法实现二维角参数的估计需要两个子阵对,且二者具有不同的距离矢量。综上分析可知利用ESPRIT算法实现盲极化二维角参数估计的条件为
1) 构建出具有不同距离矢量的两对子阵;
2) 两对子阵的距离矢量与天线单元方向图无关;
3) 实现参数配对。
共形阵列天线中的阵元设置与共形载体的几何形状有关,靠实际阵元构建两对具有不同距离矢量的子阵对不易实现,然而利用四阶累积量的阵列扩展性,通过虚拟阵元可方便构造适合ESPRIT算法的子阵对,进而完成共形阵列天线的DOA估计。
从式(12)中选择阵元构成导向矢量如下
b1(θ,φ) =[r1r2exp{-jk0(p1-p2)·u},
r3r4exp{-jk0(p3-p4)·u},
…,r2k-1r2kexp{-jk0(p2k-1-p2k)·u}]
(16)
b2(θ,φ)=[r2r1exp{-jk0(p2-p1)·u},
r4r3exp{-jk0(p4-p3)·u},
…,r2kr2k-1exp{-jk0(p2k-p2k-1)·u}]
(17)
若:
p1-p2=p3-p4=…
=p2k-1-p2k=Δp
(18)
r1r2≠r3r4≠…≠r2kr2k-1
(19)
且
r2k-1(θi,φi)r2k(θi,φi)
≠r2k-1(θj,φj)r2k(θj,φj)
(20)
对比式(16)与式(17)可知,构成b1(θ,φ)与b2(θ,φ)的相应阵元的距离为2Δp,即此子阵对的距离为2Δp,与单元方向图无关。若此距离不大于入射信号的半个波长,则在此基础上利用ESPRIT算法可实现共形阵列天线的盲极化高分辨DOA估计,式(20)用以保证协方差矩阵的秩与入射信号的个数相同。通过此方法可方便构建子阵对,针对不同几何形状(以柱面、锥面与球面共形载体为例)的共形载体其阵元设置与子阵选择方法如下:
由于共形载体的遮蔽效应,每个阵元并不能保证接收到任意方位信源的辐射信号。为了实现方位角的360度覆盖,克服共形载体的遮蔽效应,可将共形阵列天线划分为若干个子阵,每个子阵覆盖一定的角度范围,并保证每个子阵的所有阵元可接收此角度范围内所有方位的入射信号,这样每个子阵就不再受载体遮蔽效应的影响,可实现其所负责角度范围的方位估计,然后通过综合每个子阵的估计结果即可获得全方位的角度估计。本文将共形阵列天线划分为三个子阵,每个阵列负责120度(在此阵列的坐标系中对应方位角范围为30°~150°)的方位角覆盖,因为划分的每个子阵参数估计过程完全相同,只针对一个子阵展开算法讨论,其他同理可得。
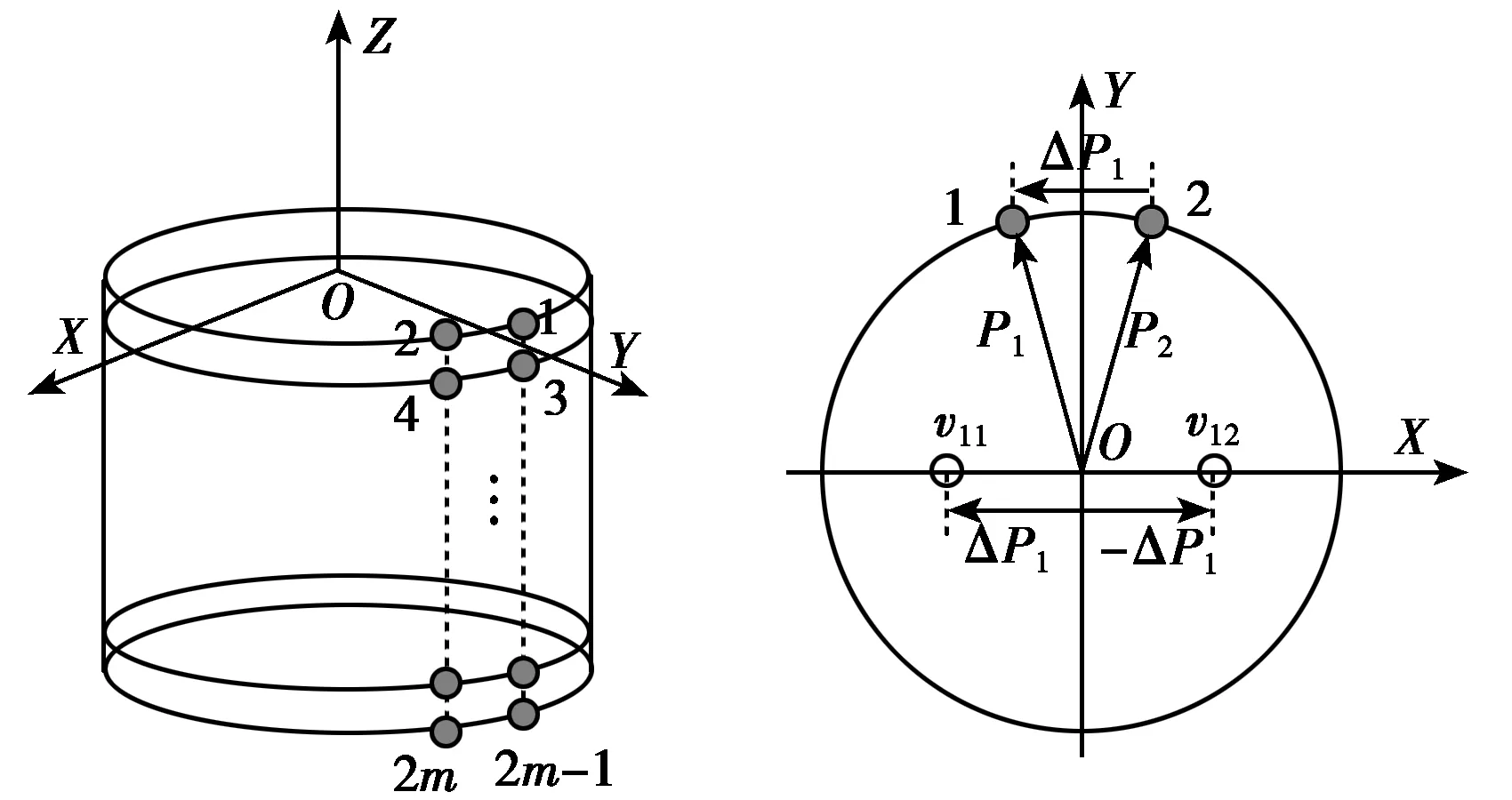
1) 柱面共形载体的阵元设置与子阵对构建
柱面共形载体上的阵元设置如图1所示:柱面共形阵列天线的全局坐标原点在柱面上底面圆心位置,坐标轴X,Y,Z如图1(a)中所示,每个柱面横截面圆周上放置两个天线单元,且其间隔为ΔP1=λ/4(如图1(b)中所示),放置天线单元的横截面圆周之间的距离为ΔP2=λ/4(如图1(c)中所示)。在图1(a)所示阵列结构前提下,应用四阶累积量的阵列扩展性可得扩展后导向矢量(如式(12)所示),图1(b)中的虚拟阵元v11,v12为实际阵元1,2扩展获得,图1(c)中的虚拟阵元v21,v22为实际阵元1,3扩展获得。以v11为第一对子阵中一子阵的第一个阵元,以v12为第一对子阵中二子阵的第一个阵元,以v21为第二对子阵中一子阵的第一个阵元,以v22为第二对子阵中二子阵的第一个阵元。通过对扩展后导向矢量中元素(对应着实际或者虚拟阵元)的适当选择,即可获得两对子阵,分别具有距离为ΔP1与ΔP2,且满足ΔP1垂直ΔP2,此特殊关系给DOA求解带来了极大的方便,子阵对的导向矢量形式如式(16)~式(20)所示。
(a) (b)
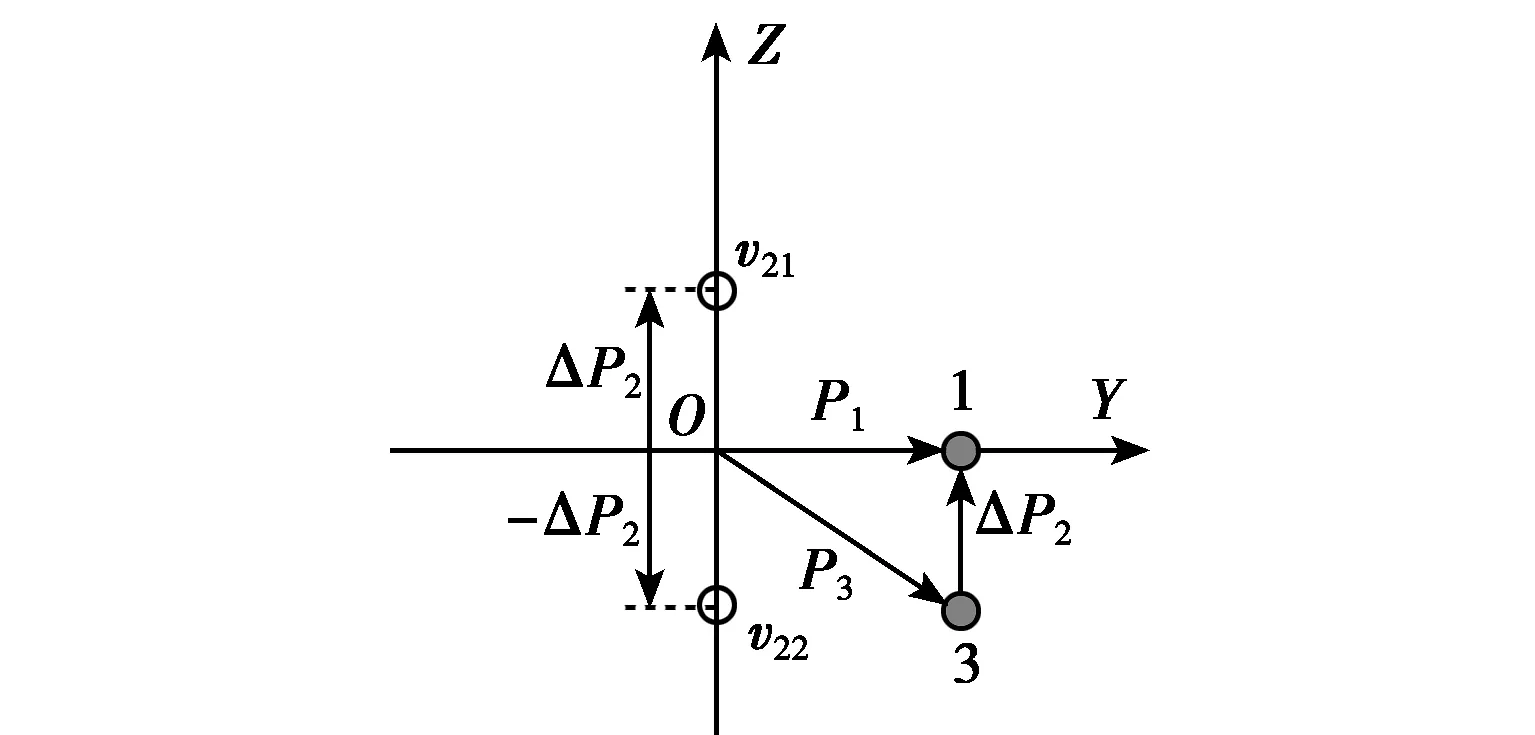
(c)图1 柱面共形载体上的阵元设置
2) 锥面共形载体的阵元设置与子阵对构建
阵元设置如图2所示:锥面共形阵列天线的全局坐标原点在锥面顶点位置,坐标轴X,Y,Z如图2(a)中所示,每个横截面圆周上放置三个天线单元,且左右两个(如1与2,3与4,…,2m与2m-1)间隔为ΔP1=λ/4(如图2(b)中所示);每个横截面圆周上中间位置阵元与相邻圆周上中间阵元间隔为ΔP2=λ/4,且各圆周上中间阵元在同一母线上(如图2(a)、2(c)中所示)。在此阵列结构下,同理柱面共形阵列天线子阵选择,即可获得锥面共形阵列天线的两对子阵。两对子阵的距离分别为ΔP1与ΔP2(如图2(b)、2(c)中所示),且满足ΔP1垂直ΔP2.
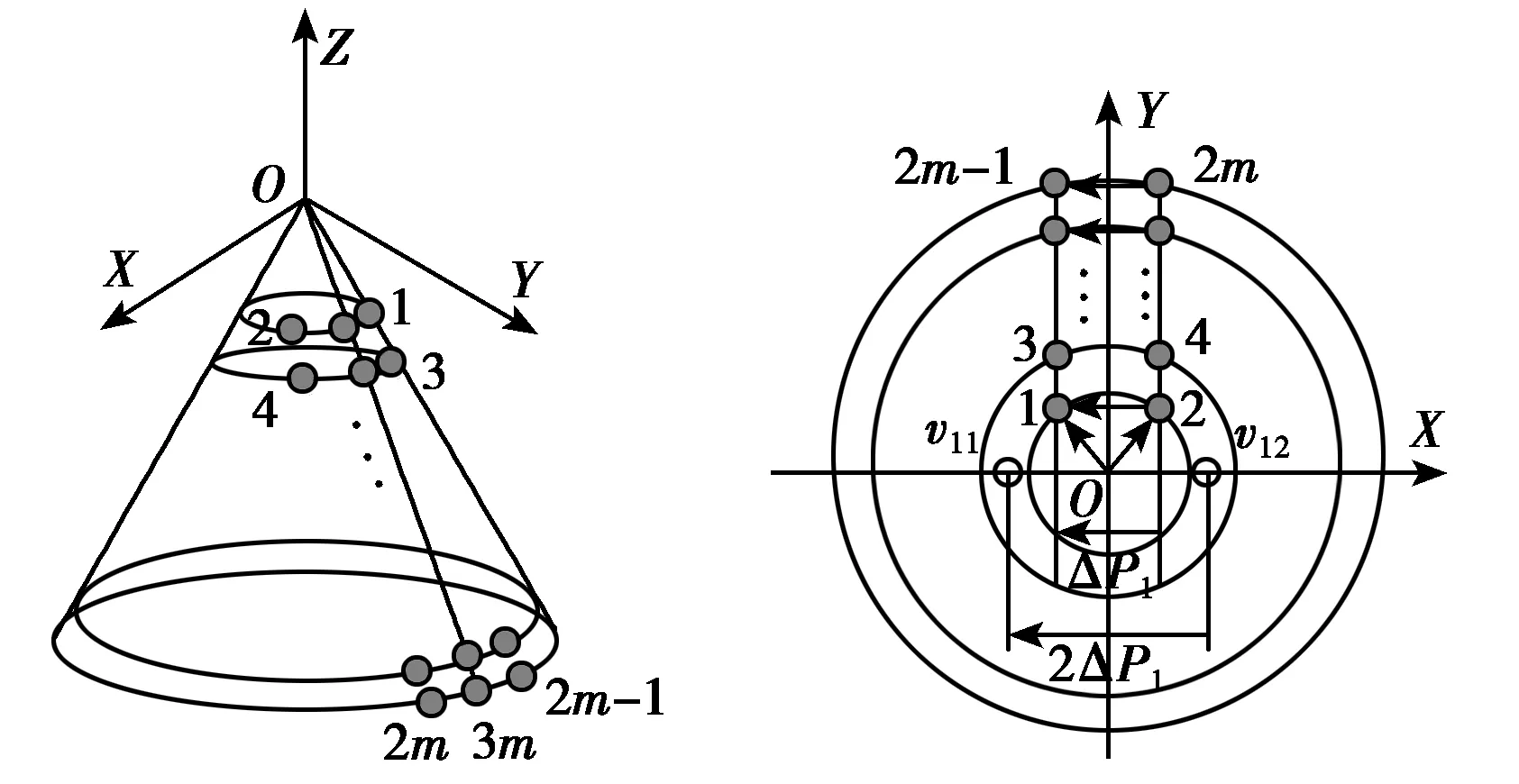
(a) (b)
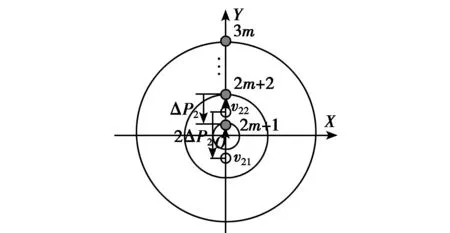
(c)图2 锥面共形载体上的阵元设置
3) 球面共形载体的阵元设置与子阵对构建
球面共形载体上的阵元设置如图3所示:球面共形阵列天线的全局坐标原点在球心位置,坐标轴X,Y,Z如图3(a)中所示,球形载体上天线单元放置分为两部分,一部分为1~2m号阵元构成,其每两阵元间距如图3(b)所示:1与2,3与4,…,2m-1与2m的间距为ΔP1=λ/4;另一部分为1,2,3,4,2m+1,2m+2,…,4m-5,4m-4号阵元构成,其每两阵元间距如图3(c)所示(仅以2m+1与2m+2号两阵元示意,其他同理):1与3,2与4,2m+1与2m+2,…,4m-5与4m-4的间距为ΔP2=λ/4。第一部分阵元构成第一对子阵,第二部分阵元构成第二对子阵。两对子阵间距分别为ΔP1与ΔP2(如图3(b)、3(c)中所示),且满足ΔP1垂直ΔP2.
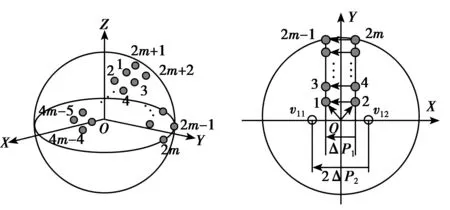
(a) (b)
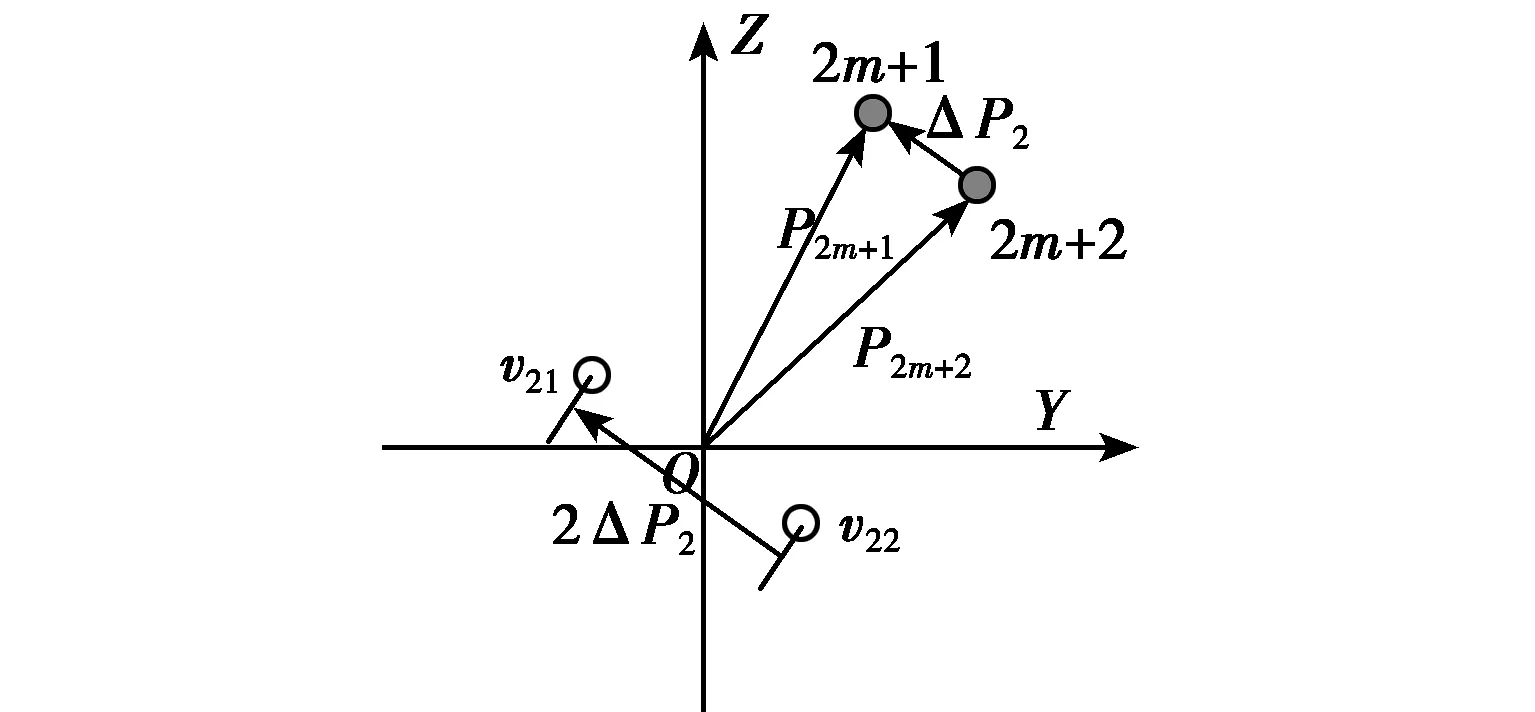
(c)图3 球面共形载体上的阵元设置
由上述分析可知,对常用的共形载体(柱面、锥面与球面)均可构建两对子阵对,且二者的距离矢量ΔP1,ΔP2不同,在此基础上利用ESPRIT算法,通过参数配对,即可实现共形阵列天线的盲极化DOA估计。
4.2 盲极化DOA估计算法
由上述给出的阵元排列方式与子阵对构建方法可获得ESPRIT算法所必须的阵列结构,在此基础上本节将以柱面共形阵列天线为例,详细推导共形阵列天线的盲极化DOA估计方法。
图1所示的柱面共形阵列天线接收的快拍数据由式(4)~式(10)所示,其中入射信号服从零均值独立非高斯分布,噪声为加性高斯噪声,且与信号相互独立。由式(4)表示的快拍数据结合式(13)可求得阵列扩展后的协方差矩阵Rcum4.从扩展后阵列中选择阵元构成如下子阵(以导向矢量的形式表示)
b11(θi,φi) =[r1r2exp{-jk0(p1-p2)·ui},
r3r4exp{-jk0(p3-p4)·ui},…,
r2m-1r2mexp{-jk0(p2m-1-p2m)·ui}]
=[r1r2exp(-jk0Δp1·ui),
r3r4exp(-jk0Δp1·ui),…,
r2m-1r2mexp(-jk0Δp1·ui)]
(21)
b12(θi,φi) =[r2r1exp{-jk0(p2-p1)·ui},
r4r3exp{-jk0(p4-p3)·ui},…,
r2mr2m-1exp{-jk0(p2m-p2m-1)·ui}]
=[r2r1exp(jk0Δp1·ui),
r4r3exp(jk0Δp1·ui),…,
r2mr2m-1exp(jk0Δp1·ui)]
(22)
b21(θi,φi) =[r1r3exp{-jk0(p1-p3)·ui},
r3r5exp{-jk0(p3-p5)·ui},…,
r2m-3r2m-1exp{-jk0(p2m-3-p2m-1)·ui}
r2r4exp{-jk0(p2-p4)·ui},
r4r6exp{-jk0(p4-p6)·ui},…,
r2m-2r2mexp{-jk0(p2m-2-p2m)·ui}]
=[r1r3exp(-jk0Δp2·ui),
r3r5exp(-jk0Δp2·ui),…,
r2m-3r2m-1exp(-jk0Δp2·ui),
r2r4exp(-jk0Δp2·ui),
r4r6exp(-jk0Δp2·ui),…,
r2m-2r2mexp(-jk0Δp2·ui)]
(23)
b22(θi,φi) =[r3r1exp{-jk0(p3-p1)·ui},
r5r3exp{-jk0(p5-p3)·ui},…,
r2m-1r2m-3exp{-jk0(p2m-1-p2m-3)·ui},
r4r2exp(-jk0(p4-p2)·ui),
r6r4exp(-jk0(p6-p4)·ui),…,
r2mr2m-2exp(-jk0(p2m-p2m-2)·ui)}]
=[r3r1exp(jk0Δp2·ui),
r5r3exp(jk0Δp2·ui),…,
r2m-1r2m-3exp(jk0Δp2·ui),
r4r2exp(jk0Δp2·ui),
r6r4exp(jk0Δp2·ui),…,
r2mr2m-2exp(jk0Δp2·ui)]
(24)
式中:Δp1,Δp2如图1所示,且|Δp1|=|Δp2|=λ/4。各天线单元方向图满足式(19)与式(20),式(21)~式(24)给出了两对具有不同距离矢量2Δp1,2Δp2的子阵对
b11(θi,φi)=b12(θi,φi)exp(-jk02Δp1·ui)
(25)
b21(θi,φi)=b22(θi,φi)exp(-jk02Δp2·ui)
(26)
对应式(4)得子阵l11接收数据如下
X11=B11S+N11
=(B11θKθ+B11φKφ)S+N11
(27)
子阵l12接收数据如下
X12=B12S+N12
=(B12θKθ+B12φKφ)φ1S+N12
(28)
φ1=diag[exp(-jw11),…,exp(-jw1n)]
(29)
w1i=(2π/λ)2Δp1·ui=4πΔp1·ui/λ
=π[sin(θΔp1)cos(φΔp1)sin(θi)cos(φi)+
sin(θΔp1)sin(φΔp1)sin(θi)sin(φi)+
cos(θΔp1)cos(θi)]
(30)
式中:B11,B12分别由式(21)、式(22)接收不同方位的入射信号构成。同理由第二对子阵对l21,l22可得
φ2=diag[exp(-jw21),…,exp(-jw2n)]
(31)
w2i=(2π/λ)2Δp2·ui=4πΔp2·ui/λ
=π[sin(θΔp2)cos(φΔp2)sin(θi)cos(φi)+
sin(θΔp2)sin(φΔp2)sin(θi)sin(φi)+
cos(θΔp2)cos(θi)]
(32)
(33)
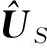
(34)

=span{B12}
(35)

=span{B22}
(36)
式中:B21,B22分别由式(23)、式(24)接收不同方位的入射信号构成;span{(·)}表示由矩阵(·)的列矢量张成的空间。由于有
B12=B11φ1
(37)
B22=B21φ2
(38)
所以
(39)
(40)
对应最小二乘ESPRIT算法有:
(41)
(42)
式中:(·)-1表示取(·)的逆矩阵。用矩阵Ψ1,Ψ2的特征值分别构成对角阵一定等于矩阵φ1,φ2.故可通过获得旋转不变关系矩阵Ψ1,Ψ2,结合式(30)与式(32)求解二维角参数。设矩阵Ψ1,Ψ2的第i个特征值分别为t1i,t2i则有
exp(-jw1i)=t1i
(43)
exp(-jw2i)=t2i
(44)
由图3可知,θΔp1=90°;φΔp1=180°;θΔp2=0°;φΔp2=90°结合式(30)、式(32)、式(43)、式(44)有
θi=acos[angle(t2i)/π]
(45)
φi=acos{angle(t1i)/[-πsin(θi)]}
(46)

4) 利用式(41)与式(42)求得旋转不变关系矩阵ψ1,ψ2;
5) 通过矩阵ψ1,ψ2的特征值分析得到特征值t1i,t2i,以及特征矢量矩阵T1,T2;
6) 利用T1,T2的相关性对特征值进行参数配对;
7) 利用式(45)与式(46)求得二维角参数,此时估计结果的单位为弧度。
借鉴上述推导过程,同理可得锥面与球面共形阵列天线的盲极化DOA估计方法。
5.仿真实验
上述各节给出了阵元设置方法,并详细推导了盲极化DOA估计算法,给出了算法步骤。本节以柱面共形阵列天线为例,进行100次Monte Carlo仿真实验,进一步验证算法的有效性。其中,估计方差定义为:估计值与估计均值之差的均方值。
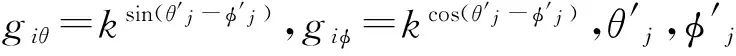
2) 仿真结果:见图4、图5、图6。
3) 结果分析:在其他条件相同时,估计效果随着快拍数与阵元个数的增加以及信噪比的改善而逐渐变好。当快拍数较小时(L=200)估计均值较好,但方差很大(如图4(a)所示);当快拍数增加到L=1000时,估计方差有明显减小,均值也有所改进,二者均达到了较好的估计效果(如图5(a)所示);当快拍数增加到L=3000时,估计效果非常好,均值基本等于真值,估计方差很小(如图6(a)所示)。信噪比的改善对估计效果有较明显的影响,当信噪比SNR=30 dB时,即使快拍数很小,也获得了很好的估计效果(如图5(c)所示)。阵元个数的增加对估计效果亦有很大影响,随阵元个数的增多,估计效果都得到很好的改善(如图4(a)、4(b)与5(a)、5(b)以及6(a)、6(b)所示)。
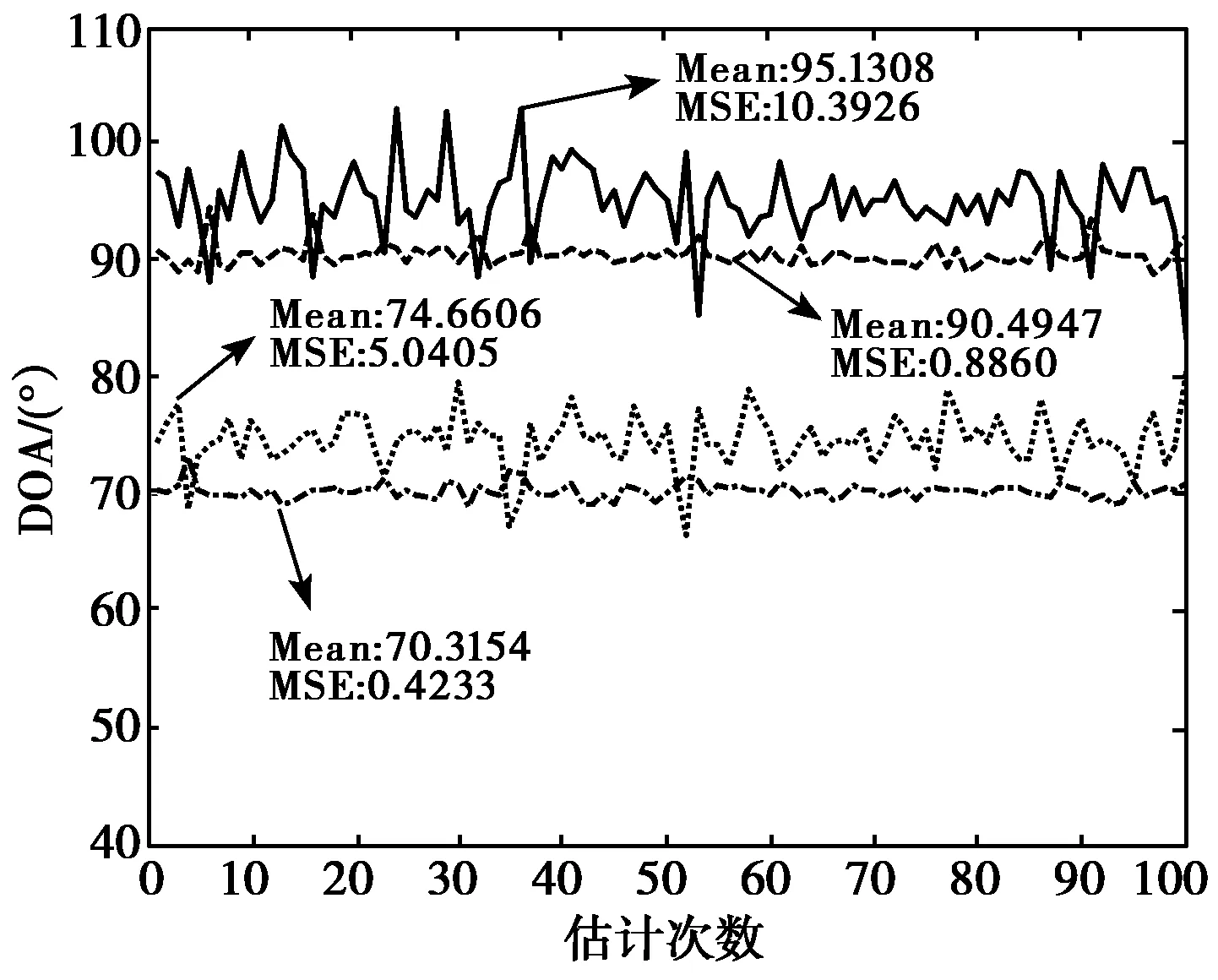
(a) SNR=20 dB m=8
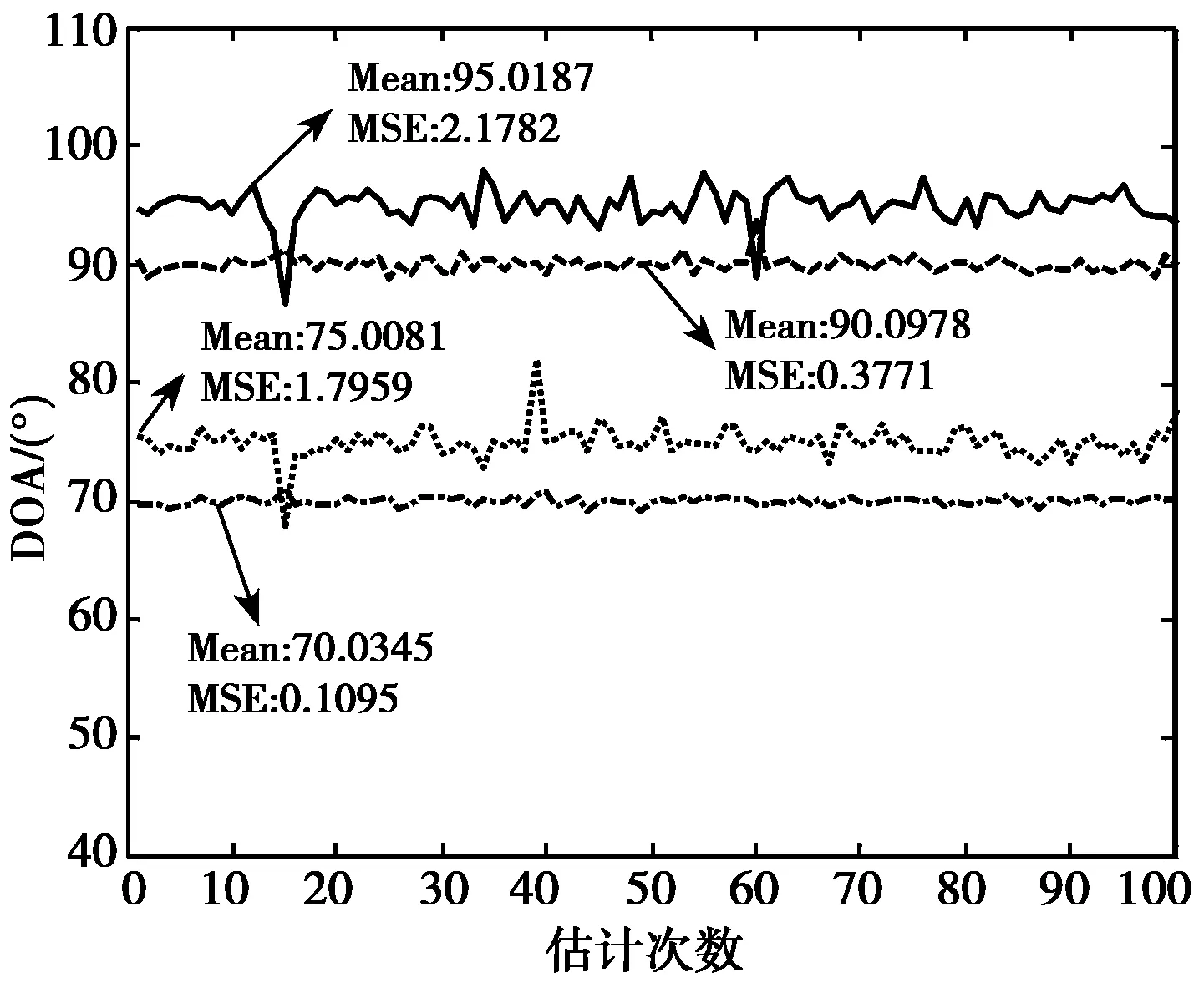
(b) SNR=20 dB m=16

(c) SNR=30 dB m=8图4 快怕数L=200时的估计结果
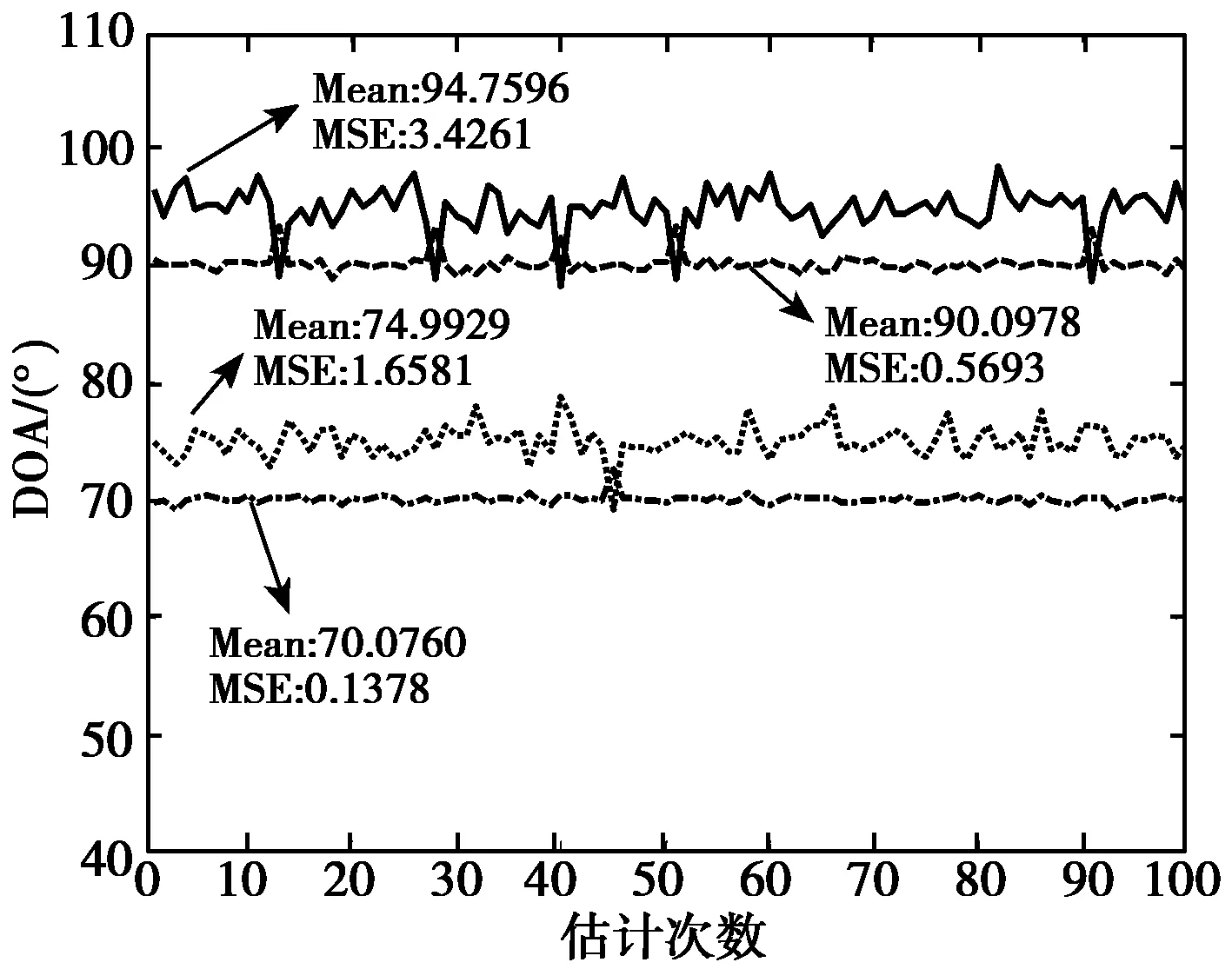
(a) SNR=20 dB m=8
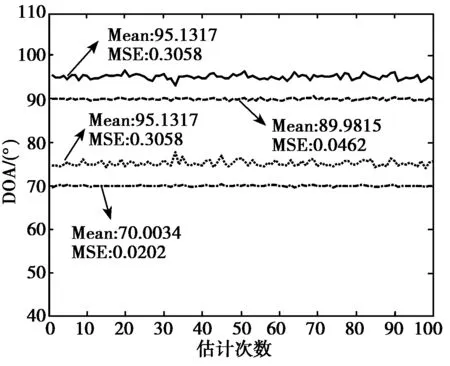
(b) SNR=20 dB m=16
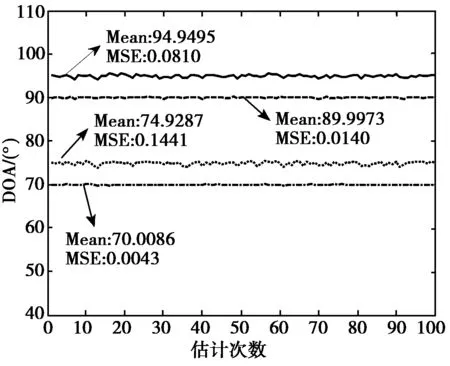
(c) SNR=30 dB m=8图5 快怕数L=1000时的估计结果
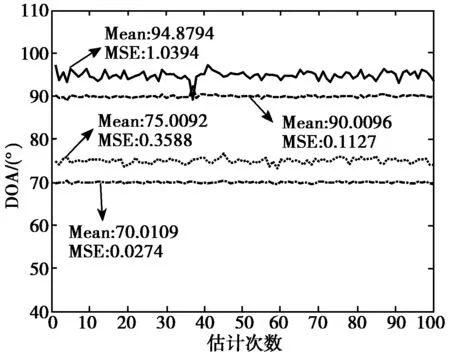
(a) SNR=20 dB m=8
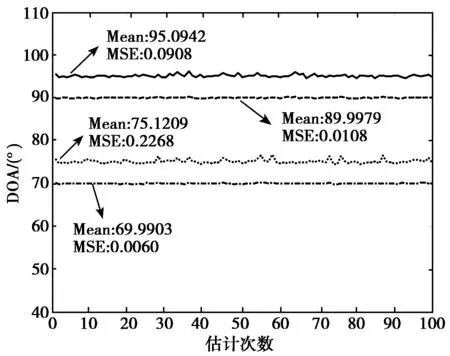
(b) SNR=20 dB m=16

(c) SNR=30 dB m=8图6 快怕数L=3000时的估计结果
6. 结 论
本文针对共形阵列天线高分辨DOA估计的特点,通过合理的阵元排列方式,利用快怕数据的四阶累积量与ESPRIT算法,将信源极化参数与二维角参数去耦合,提出了一种适合于多种几何结构的共形阵列天线盲极化DOA估计算法。以柱面共形阵列天线DOA估计为例,详细推导了算法机理,给出了算法步骤。计算机Monte Carlo仿真实验表明:所提方法可以很好地解决共形阵列天线盲极化DOA估计问题,达到了很好的效果,从而验证了所提算法的有效性。但是,计算快拍数据的四阶累积量是算法的运算瓶颈,引入高速、高效的四阶累积量运算方法,进一步减小算法复杂度将是后续工作的重点。
[1] JOSEFSSON L P. Persson Conformal array antenna theory and design [M]. Canada: Wiley-IEEE Press, 2006.
[2] WORMS J G . Super resolution with conformal broadband antenna arrays [C]//Proc. 2002 IEEE Radar Conf. Long Beach, CA, 2002: 425-431.
[3] DO-HONG T, FISCH W, RUSSER P. Direction finding using spectral estimation with arbitrary antenna arrays[C]//Proceedings of IEEE MTT-S International Microwave symposium Digest . 2001: 1387-1390.
[4] HWANG S, SARKAR T K. Direction of Arrival (DOA) estimation using a transformation matrix through singular value decomposition[C]//Proceedings of IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetic , 2005: 353-356.
[5] 杨 鹏, 杨 峰, 聂在平,等. MUSIC算法在柱面共形天线阵中的应用研究[J]. 电波科学学报, 2008, 23(2): 288-291.
YANG Peng, YANG Feng, NIE Zaiping, et al. DOA estimation of cylindrical conformal array by MUSIC algorithm [J]. Chinese Journal of Radio Science, 2008, 23(2): 288-291. (in Chinese)
[6] YANG Peng, YANG Feng, NIE Zaiping. DOA estimation with sub-array divided technique and interpolated ESPRIT algorithm on a cylindrical conformal array antenna [J]. Progress in Electromagnetics Research, 2010, 103: 201-216.
[7] WANG Buhong ,GUO Ying , WANG Yongliang. Frequency-invariant pattern synthesis of conformal array with low cross-polarization [J]. IET Microwaves, Antennas & Propagation, 2008, 2(5):442-450
[8] 王布宏, 郭 英, 王永良,等. 共形天线阵列流形的建模方法[J]. 电子学报, 2009, 37(3): 481-484.
WANG Buhong, GUO Ying,WANG Yongliang, et al. Array manifold modeling for conformal array antenna [J]. Acta Electronica Sinica, 2009, 37(3): 481-484. (in Chinese)
[9] 齐子森, 郭 英, 王布宏, 等. 共形阵列天线MUSIC算法性能分析[J]. 电子与信息学报, 2008, 30(11): 2674-2677.
QI Zisen, GUO Ying, WANG Buhong, et al. Performance analysis of MUSIC for conformal array [J]. Journal of Electronics & Information Technology, 2008, 30(11): 2674-2677. (in Chinese)
[10] 齐子森, 郭 英, 姬伟峰, 等. 锥面共形阵列天线盲极化DOA估计算法[J]. 电子学报, 2009, 37(9): 1919-1925.
QI Zisen, GUO Ying, JI Weifeng, et al. Blind DOA estimation algorithm for conical conformal array antenna with respect to polarization diversity [J]. Acta Electronica Sinica, 2009, 37(9): 1919-1925. (in Chinese)
[11] ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques [J]. IEEE Trans. on ASSP, 1989, 37(7): 984-995.
[12] DOGAN M C, MENDEL J M. Applications of cumulants to array processing-part Ⅰ: aperture extension and array calibration [J]. IEEE Trans. on SP, 1995, 43(5):1200-1216.
[13] PORAL B, FRIEDLANDER B. Direction finding algorithms based on high-order statistics [J]. IEEE Trans. on SP, 1991, 39(9): 2016-2023.
[14] 董 轶, 吴云韬, 廖桂生. 一种二维到达方向估计的ESPRIT新算法[J]. 西安电子科技大学学报(自然科学版),2003,30(5):569-573.
DONG Yi, WU Yuntao, LIAO Guisheng. A novel method for estimating 2-D DOA [J]. Journal of Xidian University(Nature Science Edition), 2003,30(5):569-573. (in Chinese)

