利用体面结合积分方程分析 表面波天线辐射问题

肖 科 赵 菲 邱 磊 柴舜连 毛钧杰

(国防科技大学电子科学与工程学院，湖南 长沙 410073)

1. 引 言

人工材料定义为可展现出自然界难以呈现电磁特性的一种人工电磁结构，目前成为研究热门的人工材料包括光子带隙材料、左手材料以及各向异性材料[1-3]，这些新材料都已广泛应用于微波、光学器件的研究中。然而，人工材料受限于高损耗、窄带宽、各向异性等特性，使得它较难应用于微波器件的制作中。

基于二维介质基板人工材料的应用可以较好地解决以上问题[4-5]。文献[1]中曾认为周期结构天线在表面波带宽内，因周期结构表面等效于普通导体表面，所以天线的辐射效率低，输入反射较大，不利于实际应用。但是经过对表面波特性的研究，发现表面波可以在周期结构的边缘或棱角辐射，论文[6,7]在此基础上提出了一种基于微带周期结构的表面波天线，但是，该文并没有对表面波天线的辐射机理进行更为深入的研究，并且，没有区分漏模频带和表面波频带。文章提出了表面波频带的概念，并且，利用体面混合积分方程和快速算法[8]，有效求解分析表面波天线的辐射特性以及电流分布情况，进而，提出基于表面波频带内的新型小型化天线设计思路。

对于微带天线辐射问题，常用的电磁分析方法主要分为半解析方法和全波方法，其中半解析方法通常假设微带天线具有无限大的接地面，通过推导直接针对源电流的并矢格林函数求解辐射问题[9]，这种方法在建模阶段已经做了不少近似，且不能考虑有限接地面的影响，计算准确度不够。至于有限周期结构问题，此类方法更加难以应用。全波方法，如矩量法、有限元法、时域有限差分法等，都可以有效分析有限大接地面的电磁问题，并且已经有不少采用相关电磁算法的商业软件出现。其中，基于面积分方程或者体面结合积分方程与矩量法结合的方法，已经大量被研究人员采用。然而，采用此方法求解电大尺寸问题时，却面临着计算复杂度过高和存储需求过大等难题，但不少快速算法的引入在一定程度上缓解了这个问题[10-11]。作者采用了一种预修正快速傅里叶变换方法来加速运算和减少存储量，并且，选用了更适于分析非均匀或者多层介质问题的体面结合积分方程分析周期结构微带天线。文章在第二节简介算法原理，在第三节分析了表面波天线辐射机理以及一类新型表面波天线。

2. 积分方程与快速算法

基于电磁场的等效原理，利用体等效原理将介质内的电通密度等效为体电流密度[12]，并且，对于介质表面覆盖的金属，采用面等效原理将金属等效成面电流密度[12]，这样等效的好处是可以采用自由空间中的并矢格林函数进行计算。这种等效方法可以分析任意非均匀各向同性介质和金属混合目标，且易于采用快速算法加速运算。

分析金属介质混合问题的体面结合积分方程如下：

(1)

(2)

式中：V表示介质体；S表示导体表面，在分析薄金属层时，可以忽略金属层的厚度，将上下表面电流合成单层电流分析，则计算的面电流实际上为金属层上下表面电流的矢量和；D(r)表示介质内电位移密度;Ei为激励电场;Es是由JS和JV计算得到的散射场，表示为

Es(r)= -jωAS(r)-▽φS(r)-

jωAV(r)-▽φV(r)

(3)

式中：矢量磁位和电标位分别表示为

(4)

(5)

式中：ρS表示由面电流散度得到的面电荷密度；ρV表示介质中感应体电荷密度。

根据矩量法基本过程，利用RWG基函数离散面电流[13]，利用SWG基函数离散体电位移密度[14]，将未知电流代入方程(1)和(2)，并利用伽略金方法计算电磁矩量[15]，就可得到包含未知面电流、体等效电流系数的方程组。然而，矩量法得到的阻抗矩阵是一个稠密阵，采用LU分解法直接求解该矩阵方程需要计算机内存为O(N2)，计算复杂度为O(N3)，分析电大尺寸问题，效率不高。采用预条件快速傅里叶加速算法之后[11]，分析纯金属或者纯介质问题，内存需求分别降为O(N1.5)或者O(N)，计算复杂度分别降为O(N1.5logN)或者O(NlogN).

3. 天线分析

3.1 表面波天线的特性

不管是常用的谐振模微带天线[16]，还是漏模微带天线[16]，由于微带结构上表面波的存在，实际的辐射方向图如图1(a)所示。其中，主模的辐射方向通常是与微带面垂直的方向，而表面波被束缚在微带表面上，波阻抗为虚数，在垂直于微带方向能量迅速衰减，故表面波能量主要分布在微带平面；并且，由于边角处的不连续性，表面波将引起边缘电流并导致边缘辐射效应，如图1(a)所示，显然，表面波的存在浪费了一部分能量，降低了辐射效率。拥有表面波禁带的高阻表面的引入可以较好解决这个问题[1,5,17]，已有不少关于高阻表面应用的文章出现。工作于表面波禁带的高阻表面抑制了该频段内表面波的传输，并防止了微带水平面内的表面波的辐射，提高了天线的效率，且能得到较好的方向图，该应用还可以解决阵列天线中表面波互耦问题。文章采用了与表面波禁带相反的思路，假设需要的辐射方向是沿微带面的，需要抑制的“杂散”辐射是垂直于微带面的，即可以通过建立一定的结构形式，使得在该频段内，没有激励起谐振模或者不传输漏模，而只存在表面波，则相当于找到了一个表面波“通带”，那么就可以得到图1(b)所示的辐射形式。

图1 主模或者表面模式辐射方向示意图

在文献[1]中，研究过TM表面波在金属表面和高阻表面的传输特性，并在同样的激励条件下给出了两种情况下的测试结果，对比文献[1]中两条测试曲线如图2所示。

图2 文献[1]中TM表面波传输特性比较

可见，在表面波阻带以下，存在一定带宽的表面波通带，对比文献[1]中高阻表面单元结构的能带结构图还可以发现，TM表面波阻带在10 GHz以上，图2(a)中表面波通带位于该表面波阻带以下，且理想情况下没有漏模存在，所以在该频段可能存在图1(b)所述的辐射形式。

3.2 天线结构及结果分析

通过观察已有文献的实验室数据可以发现[1,18,19]，周期结构的引入可以在某些频段产生表面波阻带，相应地，在某些频段也可以“增强”表面波的传输，相当于形成了表面波通带。因此，作者采用简单周期结构构建满足图1(b)所示辐射特性的天线。天线模型如图3所示，其中图3(c)是天线正反面的照片，天线基于Rogers RT/Duroid 5880介质板材，介电常数为2.2，厚度为0.7874 mm, 采用钻刻工艺进行加工。由图3所示，天线由两类周期结构单元构成，介质下表面金属敷层部分使用图3(a)所示周期单元，为二维周期分布；有上下金属敷层部分，使用图3(b)所示周期单元，为一维周期分布。周期单元的边长都为4 mm，其中，将微带线改为一维周期阵列的目的既是增加输入与图3(a)所示周期结构间的耦合，也参与了表面波的辐射。

图3所示两类结构对应的能带结构图如图4所示。从图4可见，两种结构都没有出现表面波禁带；并且，从单元A能带结构图中可知，低于6.95 GHz的频带，远离谐振频段，并且也低于漏模频段，属于表面波频段；而从单元B能带结构图中可知，低于10.32 GHz的频带，远离谐振频段，并且低于漏模频段，属于表面波频段。将这两类周期结构结合的周期结构天线，就可能在低于6.95 GHz的频段形成表面波频段。

(a)周期单元模型A (b)周期单元模型B (c)实际天线正反面图3 天线结构示意图：

(a) 对应图3单元模型A

(b) 对应图3单元模型B图4 图3所示不同周期单元对应的能带结构图

图5 天线回波损耗测试曲线

天线回波损耗测试曲线如图5所示，在3.59 GHz至5.23 GHz的频带内出现了表面波通带，对应的输入阻抗带宽为37%，而在10.3 GHz至12.5 GHz出现了漏模传输通带，在这里不对此进行讨论。需要说明的是，应用矩量法计算了3～6 GHz频带内的响应，并采用近似方法提取了S参数，即先通过馈电点采样电压电流比得到输入阻抗，再计算端口反射系数，从对比结果可知此方法不够准确。进而测试表面波频段内中心频率附近4.6 GHz频率对应

的方向图如图6(a)、(b)、(c)所示，将文中方法及HFSS计算结果与测试结果相比可知，各测试平面的主极化方向图都较为吻合，而交叉极化方向图的比较，不论是文中算法还是HFSS计算结果都和实测结果有一定程度的偏差，造成这些误差的原因主要有：1)加工误差以及测试系统误差；2)数值模型与实际天线物理特性的偏差；3)数值方法的收敛精度及数值误差。另外，测试的增益为2.24 dB，采用体面积分方程计算增益为2.83 dB，计算三维方向图如图6(d)所示，可见，此天线与单振子天线的辐射方向图类似。

为进一步了解天线金属上面的电流分布和介质内电通密度，采用体面结合积分方程分析该天线表面电流分布如图7所示。从图中可见，金属表面电流主要对称分布在图3(b) 所示x向1-D周期结构的边缘，且在x方向上同向，所以表面波辐射集中在两类周期结构的不连续性边缘上，这是辐射方向图类似于单振子天线的原因。

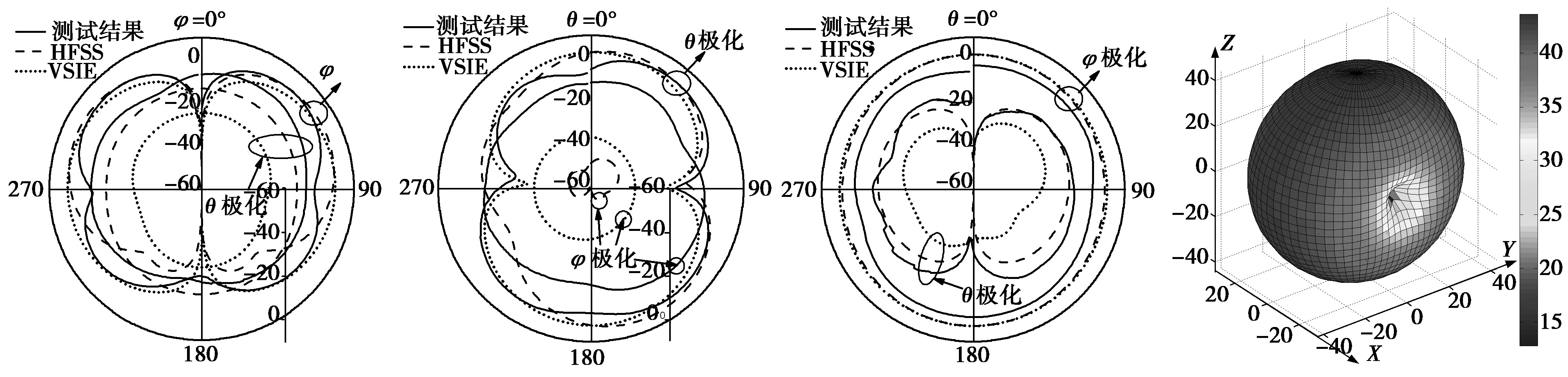
(a) xoy 面 (b) xoz 面 (c) yoz 面 (d) 3-D方向图图6 天线辐射方向图测试及仿真结果

5. 结 论

周期带隙结构的表面波阻带以下存在表面波通带，用此思路，文中设计了一类新型表面波天线，工作于表面波频段，拥有37%带宽并且有类似于单阵子天线的辐射特性，该设计思路可以用于小型化宽带高增益天线的研究。另外，文章所得电流分布图，采用商业软件计算结果不如体面结合积分方程计算结果直观，因为有限元适于直接计算未知场分布，而结合VSIE的矩量法直接计算未知电流分布，所以矩量法的优势是：可以较为灵活地计算天线的面电流和体电通量密度分布，有利于了解表面波天线的辐射机理。

[1] SIEVENPIPER D, ZHANG L J, BROAS R F J ，et al. High-impedance electromagnetic surfaces with a forbidden frequency band [J]. IEEE Trans. Microwave Theory Tech., 1999,47(11): 2059-2074.

[2] PENDRY J B. Negative refraction makes a perfect lens [J]. Phys. Rev. Lett., 2000, 85(18): 3966-3969.

[3] 赵 林，左 钰，冯一军.金属衬底多层各向异性介质电波反射特性研究[J].电波科学学报，2009，24(5): 804-807.

ZHAO Lin, ZUO Yu, FENG Yijun . Electromagnetic wave reflection of anisotropic layered media with a metallic substrate[J]. Chinese Journal of Raido Science, 2009, 24(5):804-807. (in Chinese)

[4] SHELBY R A, SMITH D R， NEMAT-NASSER S C， et al. Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial [J]. Applied Physics Lett., 2001, 78(4): 489-491.

[5] 付云起，童创明，张国华，等. 周期加载微带结构的模式分析[J].电波科学学报，2003，18(6): 607-610.

FU Yunqi, TONG Chuangming，ZHANG Guohua，et al. Mode analysis of periodically loaded microstrip structures [J]. Chinese Journal of Raido Science, 2003, 18(6): 607-610. (in Chinese)

[6] YANG F, AMINIAN A, RAHMAT-SAMII Y. A novel surface-wave antenna design using a thin periodically loaded ground plane [J]. Microwave and Optical Tech. Lett., 2005, 47(3): 240-245.

[7] AL-ZOUBI A, YANG F, AHMED K. A low-profile dual-band surface wave antenna with a monopole-like pattern [J]. IEEE Trans. Antennas and Propagat., 2007, 55(12): 3404-3412.

[8] 郭景丽，李建瀛，刘其中. 金属介质混合目标电磁特性的快速分析[J].电波科学学报，2006，21(6): 607-610.

GUO Jingli , LI Jianyin, LIU Qizhong. Fast analysis of a mixture of conducting and dielectric objects[J]. Chinese Journal of Raido Science, 2006, 21(6): 607-610. (in Chinese)

[9] TAI C T. Dyadic Green's Functions in Electromagnetic Theory [M]. San Francisco,CA: Intext Educational Publishers, 1971.

[10] 胡 俊，聂在平，王 军，等. 三维电大目标散射求解的多层快速多极子方法[J]. 电波科学学报，2004，19(5)：509-524.

HU J,NIE Zaiping,WANG Jun, et al. Multilevel fast multipole algorithm for solving scattering from 3-D electrically large object[J]. Chinese Journal of Raido Science,2004,19(5):509-524 . (in Chinese)

[11] 李 铁，张 民，吴振森，大型阵列结构电磁散射的P_FFT算法[J]. 电波科学学报，2006，21(6)：868-872.

LI Tie, ZHANG Ming, WU Zhensen . Pre-correct FFT algorithm for scattering of an large array structure [J].Chinese Journal of Raido Science,2006，21(6)：868-872. (in Chinese)

[12] BALANIS C A. Advanced engineering electromagnetics [M]. John Wiley, New York, 1989.

[13] RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape [J]. IEEE Trans. Antennas Propag., 1982, 30(3): 409-418.

[14] SCHAUBERT D H, WILTON D R, GLISSON A W. A tetrahedral modeling method for electro-magnetic scattering by arbitrarily shaped inhomogeneous dielectric bodies [J]. IEEE Trans. Antennas Propagat., 1984, 32(1): 77-85.

[15] HARRINGTON R F. Field computation by moment methods [M]. New York, Macmillan, 1968.

[16] BALANIS C A. Modern antenna handbook [M]. John Wiley & Sons., 2008.

[17] 朱方明，林青春. 新型电磁(光子)晶体贴片天线的研究进展[J]. 电波科学学报，2002，17(2): 182-186.

ZHU Fangming, LIN Qingchun . The development of novel patch antenna using photonic band-gap structures[J]. Chinese Journal of Raido Science,2002,17(2):182-186. (in Chinese)

[18] 贾宏燕，高劲松，冯晓国，等. 一种新型组合单元频率选择表面[J].光学学报，2008，28(8):1596-1600.

JIA Hongyan,GAO Jinsong,FENG Xiaoguo,et al. Novel composite element frequency selective surface[J].Acta Optica Sinica, 2008，28(8): 1596-1600. (in Chinese)

[19] 施凌飞，宗志国，许戎戎，等. 基于电容加载的圆环缝隙频率选择表面研究[J]. 电子学报，2010，38(6): 1362-1365.

SHI Lingfei , ZONG Zhiguo,XU Rongrong, et al. Research on Loaded Frequency Selective Surface with Ring Slot Elements[J]. Acta Electronica Sinica, 2010，38(6): 1362-1365. (in Chinese)