楔形体入水复变边界元数值仿真
魏照宇, 石秀华, 王生武
楔形体入水复变边界元数值仿真
魏照宇, 石秀华, 王生武
(西北工业大学 航海学院, 陕西 西安, 710072)
为了对楔形体常速入水的抨击问题进行研究, 本文在数值求解过程中, 利用了以柯西积分为积分方程的复数变量边界元法, 并使用了非线性自由面边界条件迭代法, 结合浅水近似对射流进行了处理。利用3次样条插值对自由面上的网格进行了划分, 并详细讨论了网格、控制体大小的选取及一些相关数值方法, 得到了各种不同底升角楔形体入水物体表面的压力分布和自由面隆起及射流。结果表明, 当底升角很小时物体表面压力很大, 射流又细又长, 压力分布在射流处接近零, 且没有振荡和毛刺, 说明这种射流处理方法能很好地模拟射流飞溅。
楔形体; 入水冲击; 复数变量边界元法; 非线性自由面边界条件迭代法; 底升角
0 引言
高速流固耦合冲击可以在很多应用中得到体现。被人们熟知的有甲板上浪、入水冲击、波浪冲击海洋结构物或者海岸、雷弹入水及船舶出水再入水的砰击作用。刚性楔形体的常速入水对砰击的研究具有重要意义。最早前苏联的Dobrovol′skaya基于自相似方法的速度势理论求解了楔形体常速入水, 忽略了流体重力、水的可压缩性及粘性, 得到了物体表面的压力分布和速度势[1]。Zhao和Faltinsen利用时域方法也求解了同样的问题。他们利用更精细的方法, 在高性能计算机的环境下利用边界元方法对此类问题进行了求解[2]。Tveitnes对楔形体的常速入水进行了试验研究, 并和仿真结果进行了对比[3]。楔形体入水问题还有很多值得解决的问题, 例如, 如何将2D相似解扩展到3D, 以及3自由度的楔形体自由入水和复杂2D结构和3D结构的入水, 射流从物体表面分离等都是在计算中需要考虑的问题。
本文以柯西积分作为积分方程, 利用复数变量边界元法求解了常速入水的相似解。在以往的求解中, 为了避免在自由面射流处的震荡, 以及射流变长使网格增多、网格的尺寸减小而引起的数值发散问题, 都是将射流剪掉[2], 因为射流处压力很接近大气压, 所以对物体整体运动几乎没有影响。将射流剪掉后的处理方法一般是在边界的缺口补充一个垂直于物面的单元。本文在数值仿真的过程中不将射流切掉, 而是当射流变长变薄时利用浅水近似结合非线性自由面边界条件进行处理。仿真过程中, 对不同底升角的楔形体相似解进行了研究对比, 并对涉及到的一些数值技术进行了讨论。
1 数值仿真
1.1 控制方程和边界条件
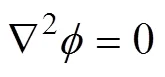
在楔形体的表面满足流体不可穿越固体边界条件
除此之外,点曲线还提供了分别调整红、绿、蓝三色通道的功能,以便我们在调整影调的同时对画面色彩精细调整。不过在这篇教程里面,我们并不打算讨论这部分功能。
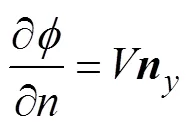
首先, 以控制面和自由面的交点为起点建立坐标和多边形弧长的3次样条公式
我校语文组开展“以地域性特色为载体的中职语文综合活动课案例研究”课题研究,我从中职语文综合活动“走进家乡文化”课堂实践进行了一些思考。
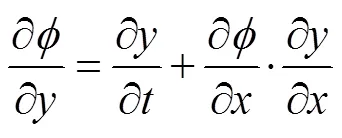
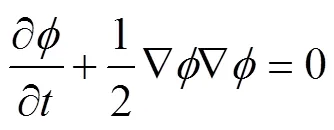
玻璃白烧制出来的效果是否平整,取决于“打玻璃白”的技术是否过硬,也需要一定的技巧。第一种就是需要掌握好标水的技法,也要熟悉笔肚所含的玻璃白多少,这样就能把握打玻璃白的速度。第二种就是在需要打玻璃白的位置先涂上煤油,煤油能使次面光滑,然后玻璃白一涂在打了煤油的次面上能迅速平整的铺满瓷面。

1.2 常速入水的相似解
当忽略流体重力时, 常速入水的楔形体在不同时间段水面隆起的形状都是相似的, 可以利用无量纲变量来进行求解, 在无量纲相似坐标系下入水物体在垂直方向上的位移始终为1。这种问题可以通过迭代法求解, 假设在初始时刻自由液面是水平的且自由面上的速度势为零, 然后通过迭代求出自由面的形状, 直至收敛即可得到相似解。
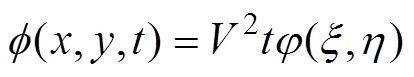
控制面上的边界条件满足流体不穿越此刚性壁边界条件
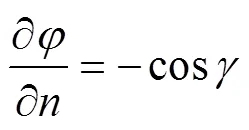
在自由面上, 运动学和动力学边界条件变为
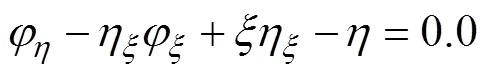
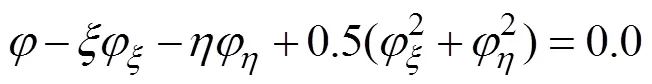
(2)在列车动载作用下,管片会产生一定的拉应力和压应力增量。其中,最大拉应力增量集中在管片标准块拱腰中部内侧和拱底块端部外侧,这些位置在自重应力作用下表现为压应力;最大压应力增量集中在管片标准块拱腰中部外侧、拱底块端部内侧及拱顶封顶块内侧,这些位置在自重应力作用下表现为拉应力。因此,在列车动载作用下,隧道管片断面的拉应力和压应力水平均存在一定程度的降低。
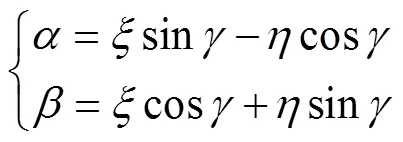
较早以前,烘托是我国绘画中的一种技术方法,利用水墨在物象的轮廓外面渲染衬托,让绘画目标更为明显。烘托应用在艺术创造过程中指的是由侧面着意描写,起到陪衬作用,凸显事物。烘托手法应用在古诗词中也较为广泛,通过烘托方法润色后让古诗更加委婉、含蓄,更具意境美。
大学课堂对知识的教授已经不仅仅体现在基础层面,更多的是一种深入式的教学。为了确保课堂教学的深度,首先老师要对所讲内容有一个深刻的认识,这样才能够以自己的思想来组织和引导这门课程的开展,同时将教学从浅显的概念上升到思想的高度[16]。
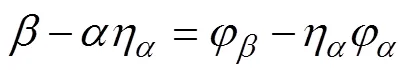
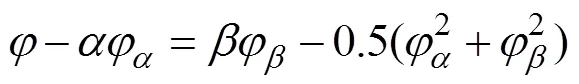
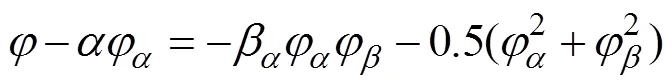
如果将式(11)和式(13)的右边看成是已知的, 则上式就可以看成是1阶常微分方程, 利用1阶常微分方程的解法得到
加强创新团队建设和创新人才培养。今年上半年,由院工会、团委推动,相继成立了由技术专家领衔组建的“劳模创新工作室”和“青年创新工作室”,分别致力于鄂尔多斯盆地致密低渗气藏勘探开发重点难点的攻关及致密气藏精细描述等相关勘探开发技术方面的创新攻关。
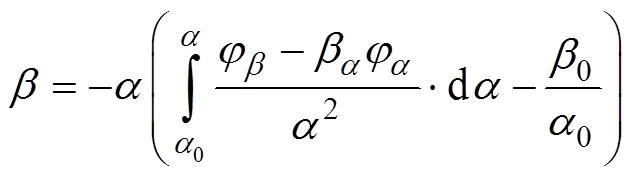
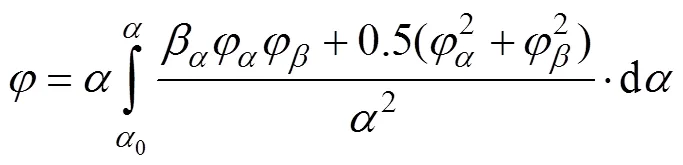
当又细又长的射流出现时, 射流区域可以结合浅水近似求解, 由浅水理论[5]可知速度势在射流上是线性变化的, 取前2项
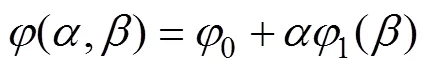
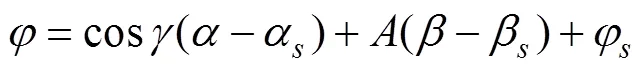

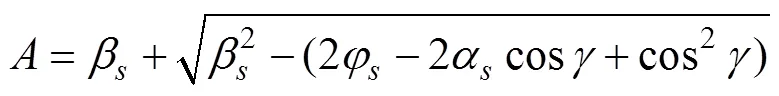
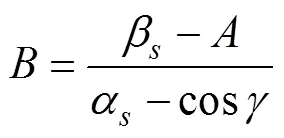
Kahneman和Tversky改变了传统理论评估总效应的做法,转而衡量一个前景的总价值V,该价值主要是通过价值函数υ(·)和决策权重函数π(·)的结合来决定的。[14]价值函数反映了结果的主观价值,决策权重函数表示与该结果概率P相对应的决策权重,它和客观概率P有着本质的区别,它反映了P对整个前景值的影响力,“是决策者根据事件结果出现的概率(p)做出的某种主观判断”[15]。这意味着决策者在进行风险决策时,至少会受到两个方面的影响:一是决策者对结果主观价值感受的影响;二是决策者对结果出现的主观概率判定的影响。
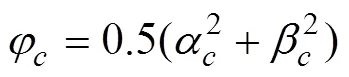
Draught Monitoring Based on Contour Cluster Analysis
2 数值方法
2.1 复数边界元法求解
和的边界值问题都需要在相似坐标系下利用复速度势在复数边界元下求解, 由柯西积分方程[6]得

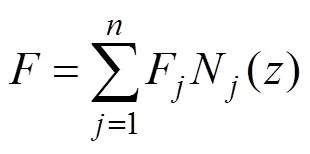
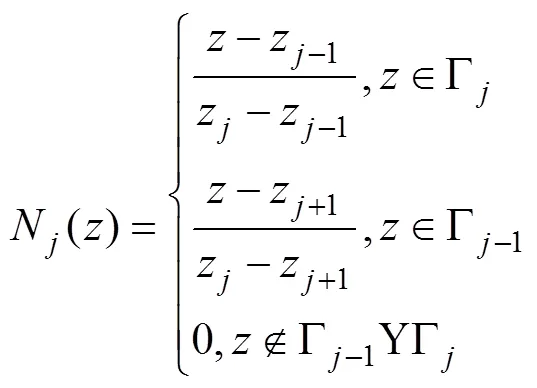
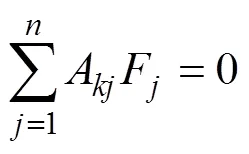
运动学边界条件规定自由表面上的水质点始终在自由表面上, 动力学边界条件规定自由面上的流体压力始终为大气压力。因为冲击持续的时间很短, 流体重力的影响相在小时间上的展开是2阶小量, 所以可以忽略[4]。令自由面上的大气压为零, 得到欧拉形式的自由面边界条件为
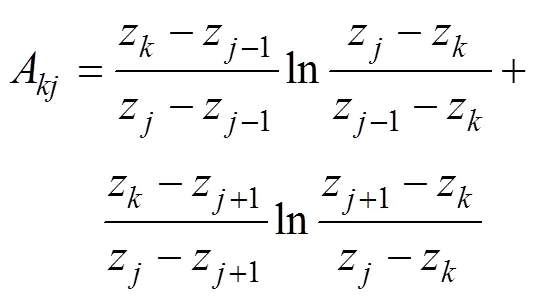

上述方程可以拆分成下面的形式
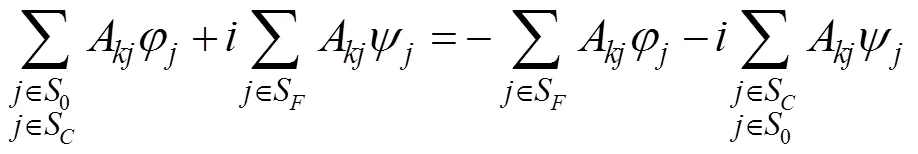
式中的系数为
每次求解矩阵方程后得到自由面上的流函数后即可利用式(14)和式(15)得到新的自由面和自由面上的速度势。再求解矩阵方程, 如此循环直至收敛为止。
2.2 3次样条插值与自由面网格的更新
在迭代时, 有的网格单元变长, 而有的则变短, 且在数值积分的过程中自由面可能会出现毛刺[8], 使得计算很难进行下去。为了使相邻单元长度的比例始终保持在1左右, 需要对自由面网格进行重新划分。
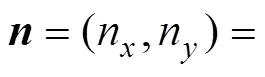
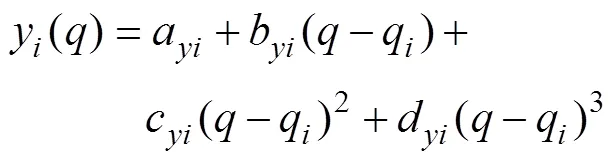
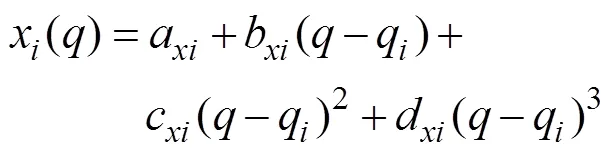
式中:Δy(k+1)=y(k+1)-y(k);Δu(k)=u(k)-u(k-1);φ(k)——伪偏导数。
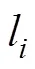
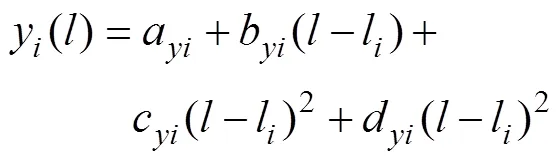
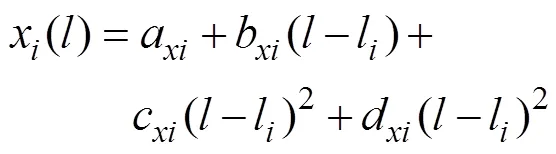
最后, 根据式(31)和式(32)得到需要的网格分布, 在靠近物面的射流上划分均匀的网格, 在远离物面的自由面上网格大小按照弧长等比增大进行划分。在得到自由面上新的坐标分布后, 可以根据相同的方法求出速度势在自由面上的分布。
另外, 在每一次的自由面更新后需要对物面重新划分网格, 网格的大小和射流上的网格保持在一个数量级。
3 数值结果与讨论
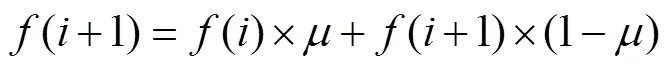
对底升角从20°到80°的情况分别进行了计算仿真。楔形体表面归一化压力/V2的分布为
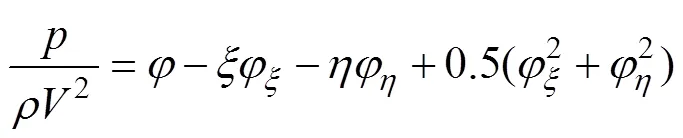
得到的楔形体表面压力分布和相似解液面隆起分别如图2和图3所示。由图2可知, 楔形体入水时的力学特性和底升角有很大的关系, 当底升角很大时, 即楔形体很尖很薄, 入水时受到的冲击压力很小, 同时激起的射流飞溅也很小。而当底升角很小时, 楔形体表面压力的分布呈现中凹的趋势, 当底升角逐渐减小时表面的压力急剧增大, 射流飞溅也又细又长。当底升角很小时, 入水可能会引起起点效应, 而文中鉴于模型求解复杂化, 没有考虑这一效应。

图3 楔形体表面无量纲压力分布
4 结论
本文建立了楔形体多种底升角的入水砰击模型, 利用复变边界元发结合自由面边界条件迭代的方法求解了对称楔形入水的相似解, 模拟了垂向入水的力学行为, 对影响砰击过程的数值参数, 包括单元的划分、控制体大小的选取以及插值等因素进行了深入而详细的讨论。可知在砰击过程中底升角对物体表面压力分布和射流飞溅的影响很大。当底升角很小时, 入水过程中受到的冲击压力很大, 飞溅的射流也很长, 而当底升角很大时, 楔形体在入水过程中受到流体的冲击压力很小, 同时飞溅起的射流也很短, 液面隆起很微小。同时, 在仿真中可知, 控制体大小的选取、插值方法的应用及网格单元划分的大小对结果的收敛性都有一定的影响, 可以避免必要的数值发散。
[1] Dobrovol¢skaya Z N. On Some Problems of Similarity Flow of Fluid with a Free surface [J]. Journal of Fluid Mechanics, 1969, 36(4): 805-829.
[2] Zhao R, Faltinsen O. Water Entry of Two Dimensional Bodies [J]. Journal of Fluid Mechanics, 1993, 246: 593- 612.
[3] Tveitnes T, Fairlie-Clarke A C, Varyani K. An Experimental Investigation Into the Constant Velocity Water Entry of Wedge-shaped Sections[J]. Ocean Engineering, 2008, 35(14-15): 1463-1478.
[4] Korobkin A A, Wu G X. Impact on a Floating Circular Cylinder[C]//Proceedings of the Royal Society, London, 2008: 2489-2514.
[5] Mei C C. The Applied Dynamics of Ocean Surface Waves [M]. NewYork: Wiley-Interscience, 1983.
[6] Hromadka T V, Lai C. The Complex Variable Boundary Element Method in Engineering Analysis[M], New York: Springer-Verlag, 1987.
[7] Grecu L, Grecu V, Demian M, Demian G. A Complex Variable Boundary Element Method for the Flow around Obstacles[C]//Proceedings of the World Congress on Engineering 2009 Vol II WCE, London, U.K July 1-3, 2009.
[8] Longuet-Higgins M S, Cokelet E D. The Deformation of Steep Surface Waves on Water: I. A Numerical Method of Computation[C]//Proceedings of the Royal Society of London A350, 1-26, 1976.
[9] Bhat R B, Chakraverty S. Numerical Analysis in Engineering[M]. Pangbourne: Alpha Science International Ltd, 2004.
Complex Variable Boundary Element Method for Numerically Simulating Water Entry of a Wedge
WEI Zhao-yu, SHI Xiu-hua, WANG Sheng-wu
(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)
To study the slamming problem of a wedge entering into water with constant speed, a complex variable boundary element method (CVBEM) based on the Cauchy integration equation is used in the numerical simulation, and the nonlinear free surface boundary conditions iteration with the shallow water approximation is also used to simulate the jet. The cubic spline interpolation is adopted to mesh the free surface. The size selections of the mesh and the control body as well as other relative numerical techniques are discussed. Consequently, the pressure distribution on wedge surface, the raise of free liquid surface and the jet pattern under different deadrise angle of sedgeare achieved when it entering into water. The results show that when deadrise angle is small, the pressure on wedge surface is great, the jet is very thin and long without shake and burr, and the pressure distribution on jet approachesto zero, which indicates a perfect simulation of jet with the proposed method.
wedge; water entry impact;complex variable boundary element method(CVBEM);nonlinear free surface boundary conditions iteration;deadrise angle
TJ631.7
A
1673-1948(2011)03-0161-06
2010-08-04;
2010-10-27.
魏照宇(1984-), 男, 在读博士, 主要研究方向为流体力学和高速物体入水冲击.
(责任编辑: 陈 曦)

