基于中枢模式发生器的仿人机器人步态规划

李正文，张国良，张维平，羊 帆

（第二炮兵工程学院 陕西 西安 710025）

近年来，仿生控制已经在机器人控制领域引起了广泛的关注，基于CPG模型的运动控制结构简单且耦合能力强，已逐渐成为多关节仿人机器人的主要控制手段。目前以CPG为背景的仿生控制仍处于起步阶段，在步态生成方法、环境反馈融合机制等方面尚存在广阔的理论研究空间[1]。

根据CPG能够在缺乏高层控制信号和外部反馈的情况下，自发产生稳定的节律性运动，无需对环境和自身建模，减少控制系统的工作量，节约工作时间等特点，笔者提出一种基于Matsuoka振荡器的中枢模式发生器。结合仿人机器人的数学模型，构建了CPG网络，并采用遗传算法作为参数调整的主要方法，仿真结果表明，该控制策略能实现仿人机器人的步态规划。

1 基于Matsuoka振荡器的中枢模式发生器构建

由于神经振荡器网络[3-4]（NeuralOscillatorsNetwork， NON）也具有无输入条件下产生周期性振荡信号的特点，因此，其常被用来模拟CPG产生信号。一般的NON由单个神经元或多个神经元相互连接构成，通过神经元之间的相互抑制和激活产生周期性的节律信号。

Matsuoka振荡器是由日本九州工学院Matsuoka提出，模型如图1所示。Matsuoka振荡器是由2个相互抑制的人工经元构成，它们的输出合成作为振荡器的输出。Matsuoka振荡器的特点是能够较好地模拟CPG的生物学特性，在没有外部激励或者外部激励小时，只需要有稳定的常激励，就能输出稳定的振荡波形。而当外部激励大于一定程度时，振荡器能够捕捉到外部的刺激信号[5]。

1.1 CPG的模拟及Matsuoka振荡器

CPG指中枢模式产生器（Central Pattern Generator)。现代神经生理学的研究证明了高等动物的节律性运动，诸如步行、游泳、呼吸、心跳等这样带有节律性，且无需外部传感输入的运动是由位于神经系统中层的脊髓和脑干的中枢神经模式产生器产生[2]。CPG的一个重要的特点是在无输入或长激励信号的情况下，产生周期性的节律信号[3]。Matsuoka振荡器可用如下方程描述[6]：

图1 Matsuoka振荡器模型Fig.1 Matsuoka oscillator model

其中x1和x2表示NON中相互抑制的神经元的内部状态；v1和v2描述了两神经元相互抑制的疲劳程度；β和ω是预先定义的常数；外部恒定激励输入c决定了NON的输出幅值；时间常数T1和T2影响输出信号的频率和外形特性。下面不经推导，给出Matsuoka振荡器的频率以及稳定振荡约束条件：

振荡器频率[7]和稳定约束条件[7]可分别表示为：

1.2 CPG网络的构建

利用CPG实现仿人机器人的运动控制以及步态规划，方法多为采用多个NON连接后构成CPG网络实现对机器人的控制。因此，如何分配和连接NON即CPG网络的搭建是使用CPG关键和难点之一。笔者将NON分配至各个关节，NON之间通过刺激彼此连接，多个NON的自组织的模式产生期望步态，并且将外部刺激直接映射到关节变量上。

本文中机器人运动过程中上身保持直立，即上肢各个关节保持初始状态，因此，仅建立机器人下肢的CPG网络。根据机器人在行走过程中脚掌始终平行于地面这一约束条件，脚踝前向关节的关节变化同髋关节和膝关节关节变化可通过几何关系确定。同时踝侧向关节变化同髋侧向关节变化可由一个侧向关节共同表示，则CPG网络如图2所示。

图2 CPG网络Fig.2 CPG network

网络方程为：

侧向关节：

左髋关节：

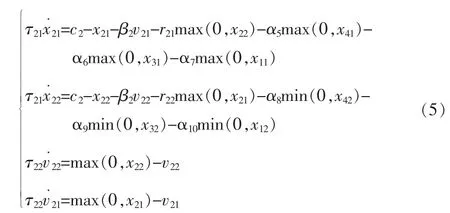
右髋关节：

左膝关节：

右膝关节：

输出方程：

网络参数为：

时间常数阵T：

根据Mastuoka振荡器分析结论，此项参数决定了周期性信号的频率。因此，可根据机器人步行的周期调节时间常数参数。笔者研究机器人在水平地面的行走问题，可根据期望的步行周期预先。

预定义常数矩阵B、Γ：

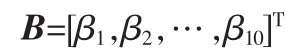
常激励c：

网络连接权矩阵A：

由（4）、（5）、（6）、（7）和（8）式可知需要的参数为 24 个。

2 基于遗传算法的CPG网络参数调整及算法的实现

2.1 CPG网络参数调整

参数调整是应用CPG方法对机器人步态进行规划的重点和难点。本文采用遗传算法作为参数调整的主要方法，为了提高算法的计算效率首先通过经验的方法寻找一定的参数变化规律，以及确定参数变化边界。同时引入相位延迟参数等辅助方法，增大可行解空间。

1）常参数确定

常激励参数主要决定了NON的输出幅值，因此它的大小主要有对应关节角变量的变化范围决定。通过对人类行走过程的观察及研究，髋部前向关节的移动范围为-30～30 deg，膝关节的移动范围为0～60 deg，侧向关节提髋使得髋侧向关节运动范围为-5～5 deg，因此，常激励 c 可确定为 c=[5，30，60，5，30，60]/57.2。考虑到人类的正常步行速度为每分钟60～75步，类比到人形机器人上的步行速度应略小于这个速度。因此，取0.15 s一步为合适。 故 T 取为：τi，1=0.3，τi，2=0.3。 取预定义常数为：βi=2.5，γi，1=2.5，γi，2=2.0[4-6]。

2）权值参数的调整

权值参数对于网络输出没有明确的映射关系，为了获取各个权值参数的有效边界，笔者采用实验的方法确定各个参数的边界。具体的方法分3步进行：1）所有参数取值相同，确定网络输出稳定振荡的参数范围；2）将各个关节的NON神经元中参数取值相同，其余NON连接参数取0，确定单个NON中参数的边界；3）综合考虑前两步所确定的参数边界，确定一个统一参数边界，这样做有利于下一步算法的编码求解。逐个参数范围确定经过实验计算结果如表1所示。

表1 确定参数边界Tab.1 Determining parameter limit

从表中可以看出，由于髋关节NON同其他NON间连接较多，故当参数同时变化时，髋关节参数变化范围小，膝关节相对较大。最终确定各个NON之间的连接参数统一为：[-5，5]。

2.2 算法实现

遗传算法的实现主要涉及到参数编码，适应度函数的确定，种群选取以及交配和变异的方法。按照GA算法随机初始化一个种群，初始的种群大小为240个个体，最大遗传2 000代，进行求解。基本求解流程如图3所示。

图3 确定参数流程图Fig.3 Flow chart of determining parameter

经过多次求解，比较各记录值可得到如下参数结果如表2所示。

表2 参数调整结果Tab.2 Results of the parameter modulation

根据以上参数，图4给出了机器人关节角的CPG的输出。

3 ADAMS仿真实验

将上述关节角运动曲线代入ADAMS虚拟样机进行仿真，仿真时间为2 s，仿真结果如图5所示。仿真表明，机器人的基本步态能够满足机器人的基本行走要求。

4 结 论

图4 CPG关节角输出Fig.4 Joint angle output of the CPG

图5 ADAMS仿真结果Fig.5 Simulation results of ADAMS

笔者对Matsuoka振荡器进行了分析，并根据仿人机器人步态规划的要求，用Matsuoka振荡器构建了CPG网络；采用遗传算法对CPG网络的参数进行了调整，得到了网络参数的调整结果，并由此得出了CPG网络对机器人步态规划的关节角输出曲线，实现了仿人机器人的基本步态规划，并通过ADAMS进行了仿真，仿真结果表明，该控制方法在仿人机器人步态规划中有一定的应用价值。

[1]于海涛.基于非线性振子的CPG步态生成器及其运动控制方法研究[D].哈尔滨：哈尔滨工业大学，2009.

[2]傅莉，谢华龙，徐心和.异构双腿行走机器人步态规划与仿真[C]//2007中国控制与决策学术年会论文集，2007：387-390.

[3]马宏绪，王剑，黄茜薇，等.基于CPG的仿人机器人运动控制方法研究[C].第六届全球智能控制与自动化大会，大连，2006.

[4]王斐斐，张奇志，周亚丽.构成CPGs的非线性振荡器模型的介绍[J].北京机械工业学院学报，2007，12（4）：31-36.WANG Fei-fei， ZHANG Qi-zhi， ZHOU Ya-li.Introduction of non-1inear oscillator model of CPGs[J].Journal of Beijing Institute of Machinery，2007，12（4），31-36.

[5]姜山，程君实，陈佳品，等.基于多目标遗传算法的仿人机器人中枢神经运动控制器的设计[J].机器人，2001，23（1）：58-62.JIANG Shan，CHENG Jun-shi，CHEN Jia-pin，etal.GA basedself-organized stable humanoid robot walking pattern generators desing[J].ROBOT，2001，23（1）：58-62.

[6]Righetti L，Ijspeert A.Programmable central pattern generators：an application to humanoid locomotion control[C].Proceedings of the 2006 IEEE International Conference on Robotics and Automation， Orlando，2006.

[7]Matsuoka K.Sustained oscillations generated by mutually inhibiting neurons with adaptation [J].Biological Cybernetics，1985， 52（4）：367-376.