永动机寻找过程中的失与得
吴兰兰
(石家庄市第二中学,河北石家庄 051430)
永动机的想法起源于印度,公元1200年前后,这种思想从印度传到了伊斯兰世界,并从那里传到了西方.永动机是指违反热力学基本定律的不能实现的发动机.历史上有不少人希望设计一种机器,这种机器不消耗任何能量,却可以源源不断地对外做功.这种机器被称为永动机.历史上,人们提出了很多种永动机的制作方案.虽然人们经过多种尝试,做了多种努力,但永动机无一例外的归于失败.但是从失败中也得到了一些收获,本文就历史上的永动机方案做一总结,以供读者赏析.
1 永动机的失败案例
1.1 滚球永动机
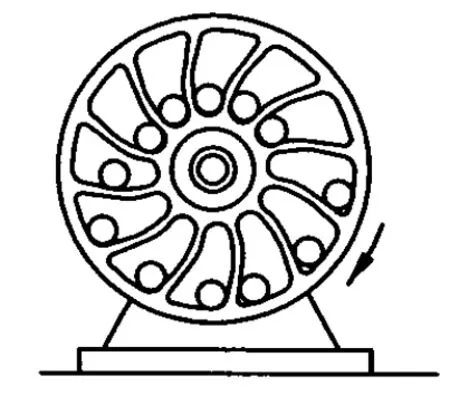
图1
例1.文艺复兴时期,意大利的达·芬奇(Leonardoda Vinci,1452-1519)设计了如图1所示的装置.他设计时认为,在轮子转动过程中,右边的小球总比左边的小球离轮心更远些,在两边不平衡的力矩作用下会使轮子沿箭头方向转动不息,而且可以不断地向外输出能量.但实验结果却是否定的.达·芬奇敏锐地由此得出结论:永动机是不可能实现的.下列有关该装置的说法中正确的是
(A)如果没有摩擦力和空气阻力,该装置就能永不停息地转动,并在不消耗能量的同时不断地对外做功.
(B)如果没有摩擦力和空气阻力,忽略碰撞中的能量损耗,给它一个初速度,它能永不停息地转动,但在不消耗能量的同时,并不能对外做功.
(C)右边所有小球施加于轮子的动力矩并不大于左边所有小球施于轮子的阻力矩,所以不可能在不消耗能量的同时,不断地对外做功.
(D)在现代科学技术比较发达的今天,这种装置可以永不停息地转动,在不消耗其他能量的基础上,还能源源不断地对外做功.
分析:该设计中,当轮子转动时,虽然右边的小球总比左边的小球离轮心更远些,但是右边小球的个数总比左边的少,实际上右边所有小球施加于轮子的动力矩等于左边所有小球施于轮子的阻力矩,轮子在不受到外力作用时将保持平衡状态.如果没有摩擦力和空气阻力,且忽略碰撞中的能量损耗,给轮子一个初速度,轮子就能依靠惯性永不停息地转动.故正确答案为(B)、(C).
1.2 浮力永动机

图2
例2.浮力是设计永动机的一个好帮手,如图2是一个著名的浮力永动机设计方案:左右的木球数目相等,绕在上下两个轮子上,可以像链条那样转动.右边的一些球放在一个盛满水的容器里.设计者认为,右边这些球浸在水里,受到了水的浮力,就会被水推着向上移动,也就带动整串球绕上下两个轮子永远转动下去.请分析其可行性.
分析:当木球由下方进入水中时,仅受到水向下的压力,而没有向上的压力,该处压强最大,所以向下的压力很大.要想使整串球永远转动下去,必须克服各处阻力做功而需要消耗能量,而这些能量又没有来源,根据能量守恒定律知,这种设计方案不可行.
1.3 磁力永动机
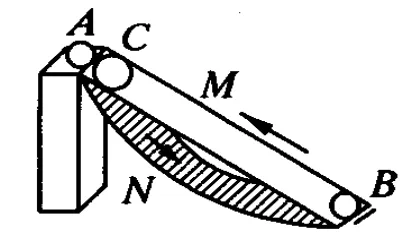
图3
例3.如图3所示为英国赛斯特城的主教约翰·维尔金斯在1670年设计的一种机器,原理是这样的:在立柱上放一个强力磁铁 A,两槽 M和N靠在立柱旁.上槽 M上端有一个小孔C,下槽N弯曲.如果在B处放一小铁球,它就会在强磁力作用下向上滚,滚到C时从小孔下落沿N回到B,开始往复运动,从而进行“永恒的运动”.关于这种机器,下列说法正确的是
(A)这种机器可以永恒运动,说明了永动机可以制造.
(B)这种机器是可以制造的,并且小球在下滑时能源源不断地对外做功.
(C)这种机器不能永恒运动,如果小球能从静止加速上升到C的话,它就不可能从C加速下滑到B,并再次从B回到C.
(D)这种机器不能永恒运动,关键是因为摩擦阻力太大,要消耗能量.
分析:这种依靠磁力与重力的永动机是不可能实现的.
首先,强力磁铁 A的磁性特别强,可以把斜面下端的铁球吸上来,铁球完全可以越过小孔C被吸引到强力磁铁A上.其次,若铁球从小孔C掉了下来,它将受到重力和磁力的共同作用,而磁力又非常大,所以铁球沿斜面做减速运动.即使小铁球运动到下端,它也决不可能绕过弯曲的地方又滚到斜面上,因此这种机器不可能永恒运动.故正确答案为(C).
1.4 电场永动机
例4.有人设计了一种如图4所示的机器:两根相互垂直的刚性绝缘细杆,相交于杆的中点,位于竖直平面内,杆的端点上各有一带正电的小球a,b,c,d.一水平的固定转轴PP′通过两杆的交点与两杆固定连接.转轴的一端有一皮带轮,通过皮带可带动别的机器转动,两杆与其端点的带电小球处在一方向与x轴平行的静电场中,电场的场强大小随 y而改变,可表示为 E=E0y.在 y=0处,场强 E=0;在y>0的区域,场强沿x轴正方向,其大小随 y的增大而增大;在y<0的区域,场强沿 x轴负方向,场强的大小随y的增大而增大.由于杆端的带电小球受到静电场的作用,相互垂直的杆将绕固定轴转动,与轴连接的皮带轮通过皮带就能带动其他机器运转.
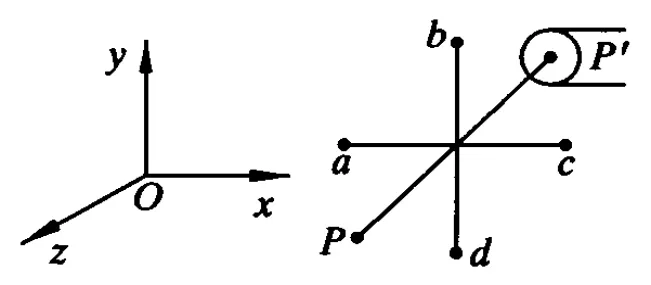
图4
设计者断言他可以实现一种不需要提供能量又能不断对外做功的永动机.你认为这种机器可能实现吗?为什么?如认为不能实现,则指出其设计中存在何种错误,并说明理由.
分析:根据能量守恒定律,任何一部机器,可以使能量从一种形式转化为另一种形式,但不能无中生有地创造能量,所以想要实现一种不需要向它提供能量但又能不断地对外做功的永动机是不可能的.题中设计方案的错误之处在于设想的静电场是不可能存在的.理由如下:
假设空间中存在这样的电场,即该电场的电场线平行,但相邻电场线的距离不等,如图 5所示.根据等势面与电场线垂直,可在该电场中找到两个等势面,如图5中的A1A2与 A3A4,则 A1A2与 A3A4平行,距离设为 d,由题意知

显然这样的静电场是不存在的.
1.5 放射性永动机
例5.如图6所示的装置是一位物理学家设计的一种使用放射性元素钍的“永动机”.它是在密闭的玻璃球壳1中,放入玻璃管2,将具有放射性的钍盐3密封在玻璃管中,4是两片彼此紧靠的金属箔,5是贴在玻璃球壳内侧的金属板,金属板接地.这个装置之所以称为“永动机”,是当两片金属箔吸收到放射线而带同种电荷时将不停地排斥,每次排斥时向左右张开,触到金属板的内壁,立即收回,如此往复,形成金属箔的“永动”.下列说法中正确的是
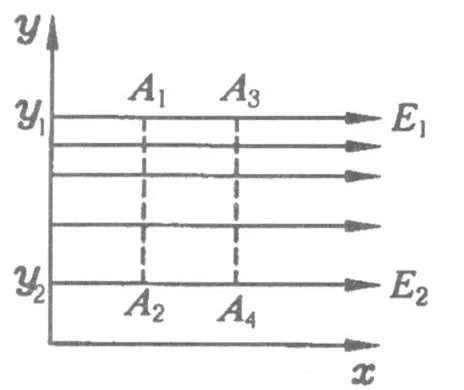
图5
(A)金属箔是由于吸收到α射线而张开的.
(B)金属箔是由于吸收到β射线而张开的.
(C)此装置可看作是第一类永动机.
(D)此装置可看作是第二类永动机.
分析:放射性元素钍具有β放射性,出射的粒子——电子被金属箔所吸收,金属箔带上同种电荷,互相排斥,金属箔张开.随着放射性元素钍不断地进行β衰变,它所提供的出射粒子——电子的数量将不断减少,所以这种装置并非“永动机”.故正确答案为(B).
2 从永动机的失败中得到的收获
找寻“永动机”固然是永远没有结果的,有趣的是,随着对于这个不可能的事情的深入了解,却也常会引出一些很好的发现.
16世纪末到17世纪初,荷兰著名学者斯台文发现了斜面上力量平衡的定律,他发现这个定律的方法,正是对上面一段话的最好说明.
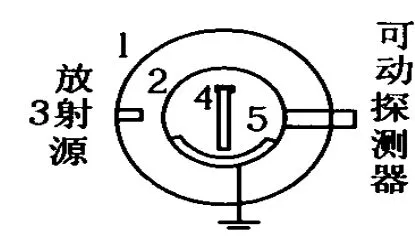
图6

图7
他发现这个斜面上力的平衡定律,并没有用到力的平行四边形法则,就只是靠图7.在一个三棱体上架着一串球,一共14个,都是一样大小的.这一串球会怎样呢?那下面挂下来的部分,不成问题,是会自己平衡的.但还有上面两部分,会不会平衡呢?换句话说,右边2个球跟左边的4个球会不会平衡?当然会的,如果说不会,那么这串球就会自动不停地从右向左移,因为一个球滑下来就有另一个球来补充,平衡也就永远不可能得到了.但是我们知道,“永动机”永不可能,这样架着的一串球是不会自己移动的,那么,右边的2个球就自然和左边的4个球平衡.初看起来这好象是一件怪事:2个球的拉力竟和4个球的相等.从这个看似奇怪的现象,斯台文发现了力学上一个重要的定律.他是这样来思考的:这一串球的两段——一段长一段短——重力不相等;长的一段跟短的一段重力的比值,恰好是斜面长的一边跟短的一边长度的比值.从这里得出一个结论,就是用绳连在一起的两个重物搁在两个斜面上,只要两个重物的重力跟这两个斜面的长度成正比,它们就可以保持平衡.
有时候,两个斜面里短的一个恰好是竖直的,于是我们就得到力学上一个有名的定律:要维持斜面上的一个物体不动,一定要在竖直面的方向上加一个力,这个力跟物体重力的比等于这个斜面的高度跟它的长度的比.
这样,从“永动机”不可能存在这一个思想出发,竟完成了力学上的一件重要发现.

