改进的运动模糊图像复原算法*

王 敏,田启川

（太原科技大学 电子信息工程学院，山西 太原030024）

运动模糊图像复原是图像恢复的重要课题之一，随着科学技术的不断进步和发展，运动模糊图像复原在天文、军事、道路交通[1]、医学图像及侦破等各个领域中的应用越来越多，要求也越来越高，从事运动模糊图像的恢复研究具有重要的现实意义。

目前，对于不同原因造成的模糊图像的复原虽然有广泛的研究，不少学者也已经提出了一些不同的具体算法，但这些方法一般仅适用于已知点扩散函数的参数情况。而对于运动模糊图像，点扩散函数通常是未知的，如果知道模糊的方向和尺度，就可以据此构造点扩散函数，用前人提出的方法进行恢复。可见，寻求一种行之有效的方法来自动鉴别运动模糊参数并实现运动模糊图像的复原是一个迫切并且必要的任务。

对运动模糊图像的盲复原，关键是精确确定点扩散函数（即模糊长度和模糊方向）并寻求一种好的复原方法。本文对模糊图像进行方向性的高通滤波 （方向微分）来判定运动模糊方向，并针对原算法运算速度慢的缺点进行改进，采用由粗到细的检测方法，从而大大提高了检测速度；然后利用边缘检测算法，计算模糊的尺度；最后采用维纳滤波算法对模糊图像进行恢复，并提出一种新的K值估计算法，将K值自动估计与传统的K取经验值相结合，进行两次维纳滤波，从而得到一个较为精确的K值。

本算法可以较好地实现图像复原，特别是针对一些模糊程度较强、人的肉眼根本不能辨别的模糊图像也能较好地恢复，具有很强的实用价值。

1 图像复原的原理

图像复原处理建立在图像退化的数学模型基础上，这个退化数学模型应该能够反映图像退化的原因。由于图像的退化因素较多，因此图像处理过程中把退化原因作为线性系统退化的一个因素来对待，从而建立系统退化模型来近似描述图像函数的退化模型，如图1所示。

若H是线性的、空间不变的过程，则退化图像在空间域的表达式为：

图1 图像退化/复原处理的模型

频域表达式为：

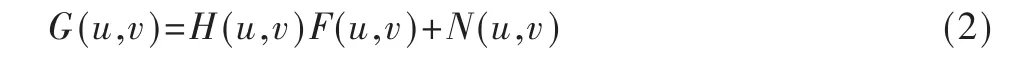
目前，图像复原的算法有逆滤波恢复[2]、维纳滤波复原[3]、有约束最小平方恢复、最小二乘方滤波复原等，本文选用维纳滤波进行图像的复原。

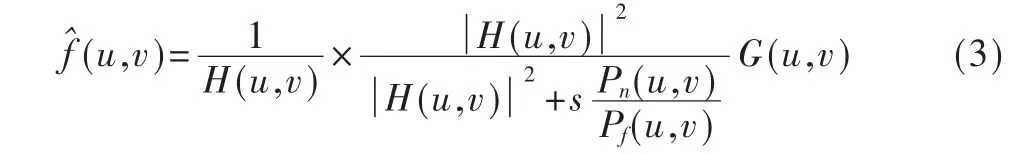
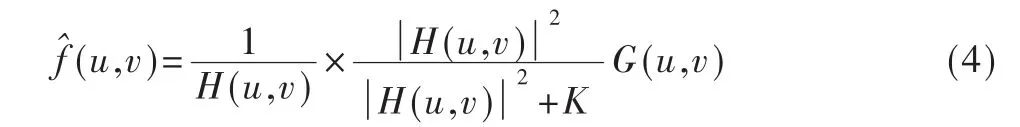
可见，用维纳滤波实现运动模糊图像的复原实质上就是求取退化函数H(u,v)和K值(信噪比)的过程，其取值的准确性将直接影响复原效果。下面介绍H(u,v)和K值的求取。

2 退化函数的确定

2.1 PSF的确定

由前面分析可知，要实现图像复原首先要建立正确的退化模型。图像复原处理可看成是一个估计过程，如果已经给出了退化图像g(x,y)并估计出点扩散函数PSF的参数(运动模糊方向和运动模糊长度)，则任意方向的匀速直线运动[4]模糊图像的点扩散函数也就可以根据任意方向匀速直线运动模糊的退化模型而唯一确定，进而由最小二乘准则使用参变维纳滤波来近似复原出f(x,y)。因此，运动模糊图像的复原，首先要确定运动模糊图像的退化模型，再根据退化模型和原始图像估计出PSF的参数,最后由相应的复原方法进行完成图像的复原工作。

对于匀速直线运动模糊图像来说，点扩展函数可以描述为：其中d为运动模糊长度，θ为运动模糊方向与水平方向角度。

2.2 模糊方向鉴别

运动方向的提取是运动模糊图像确定点扩散函数的关键因素之一。准确地估计出运动模糊方向，就可以通过图像旋转，将运动模糊方向旋转到水平轴方向，对应的运动模糊点扩散函数也随之变为一维的，运动模糊点扩散函数的估计及图像复原就由二维问题转化为一维问题，从而降低运动模糊图像复原的难度。

本文利用方向微分检测运动模糊方向的思想，并对其算法进行了改进，在保证精确度的前提下大大提高了检测速率。

2.2.1 方向微分检测模糊运动方向[5]

将原始图像看成是自相关及其功率谱是各向同性的一阶马尔科夫过程，运动模糊降低了运动方向上图像的高频成分，而对于其他方向上高频成分影响较少，且随着方向偏离越大影响越小。若对运动模糊图像进行方向性的高通滤波(方向微分)，则当滤波方向为运动方向时，由于此方向对应的高频成分最小，因此高通滤波后模糊图像能量损失最大,得到的微分图像对应的灰度值之和必然最小。因此方向微分后的图像的灰度值之和最小的方向即为运动模糊方向。方向微分示意如图2所示。

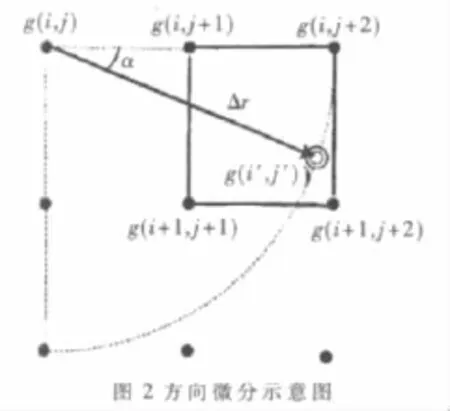
运动模糊图像为 g(i,j)，g(i′,j′)是模糊图像中以 g(i,j)为圆心、半径为Δr的半圆弧上的一点：其中Δr是进行方向微分时的微元长度，α是进行方向微分的方向角，α∈[-90°,90°]。 g(i′,j′)的值由模糊图像插值获得，其中：

对运动模糊图像g(i,j)进行方向微分(微元大小为Δr，方向角为α)，得到微分图像为：

对方向微分图像Δg(i,j)α的灰度值的绝对值求和,有:

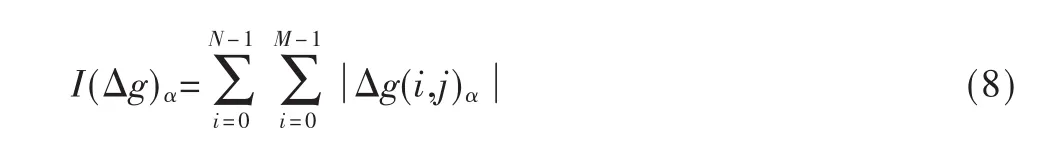
在α∈[-90°,90°]范围内按一定步长(如 1°)取α值，求出对应的微分图像灰度值的绝对值之和 I(Δg)α，并求出其中的最小值min(I(Δg)α)，则最小值 min(I(Δg)α)对应的角度即为运动模糊图像中运动模糊方向与水平轴的夹角。即：

2.2.2 快速算法实现

上述算法准确率较高，但是角度按固定步长从-90°～90°依次取值，计算耗时比较大，速度慢。本文针对这个问题对算法进行改进，采用由粗到细的方法对模糊角度进行鉴别，从而确定模糊方向。主要步骤如下：

(1)对步长初始化,令γ0=10°。 令α∈[-90°,90°]，α0=-90°；

(3)在步骤(2)中求出的新的区间内，取步长γm=1/2γm-1，返回步骤(2)；

(4)直到步长γm＜1,停止运算，最后求得的微分灰度值的绝对值最小值对应的角度即为所求。

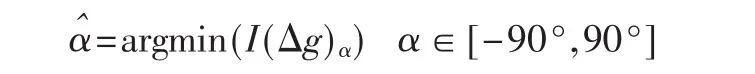
改进的模糊方向求解方法采用由粗到细的方法逐步减小感兴趣的角度区域，而将大量的非目标角度以较大的步长跳过，从而简化了运算，大大提高了检测速度。

2.3 基于边缘检测的运动模糊长度的检测

模糊长度是点扩散函数的另一个重要参数，本文将边缘检测应用于运动模糊长度的鉴别。

如图3所示，清晰图像边缘处的灰度值是急剧变化的，而运动模糊图像由于运动模糊边缘处的灰度变化相对缓慢，其对应的图像的边缘波及一个宽度区域，这个边缘区域的宽度即为运动模糊图像的模糊长度。

为了使算法具有更强的鲁棒性，在此用梯度变化来近似表示图像的边缘，进而求出模糊长度。将Prewitt边缘检测子扩展为n×n(n为奇数)的矩阵，在此用 5×5的矩阵，即 n=5。

运动模糊图像的边缘延伸到周围像素，由于运动模糊部分总是发生在模糊区域的两端,且模糊具有对称性,因此对模糊图像进行边缘检测,分别求取两端的边缘宽度，取其平均值为运动模糊长度。在此用迭代算法求取两端的边缘宽度，具体步骤如下：

(1)对图像进行边缘检测；

(2)对边缘图像进行逐行扫描，记录每行中连续边缘的边缘宽度,并对整个边缘图像中的边缘宽度进行统计，做出统计直方图，设定边缘初始宽度阈值T等于边缘宽度统计平均值以及迭代次数为n；

(3)将每一行中连续边缘的边缘宽度Tij与上述阈值进行比较,将符合0.8T≤Tij≤1.2T的边缘宽度保留下来；

(4)对每一行中最大的两个边缘宽度求和，并对所有行的和值进行统计，求出统计平均值；

(5)用步骤(4)中得到的值的1/2更新边缘宽度阈值；

(6)返回步骤(2)重复以上步骤，直到宽度值收敛或达到迭代次数。

3 改进的K值自动估计

用维纳滤波进行图像复原的关键是确定点扩散函数和K值。前文已经求出模糊角度和模糊方向，将其带入公式(5)即可得到点扩散函数h(x,y)。因此，接下来的主要的任务是求K值。

通常，K值采用经验值或通过人机对话手工调节，前者虽然简单但复原效果不佳，后者复原效果要好一些，但非常麻烦，也得不到最准确的参数值。本文采用一种自动估计K值的方法。

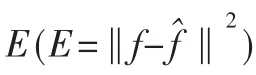
针对这种情况，本文对该K值估计算法进行了改进。首先利用传统的维纳滤波(即对K值取经验值)对原始图像进行估计，从而得到一个Pf(u,v)值，然后对模糊图像进行滤波，得到滤波后的图像，可以粗略计算Pn(u,v)值，这样就能对K值进行初步估计；再以此K值为中心设定初始值、步长及步数，进行循环，绘制E-K曲线，求曲线的极小值点，对应的K值即为所求。具体步骤如下：

(1)利用传统的K取经验值的维纳滤波方法进行第一次维纳滤波，得到一个原始图像的估计值;

(2)对模糊图像进行去噪处理，得到去噪后的图像，将模糊图像与去噪后的图像相减，认为其值为噪声；

(3)利用上述两步计算得到的 Pf(u,v)、Pn(u,v)进行 K值的初步估计；

(4)以步骤(3)计算的K为中心，确定初始K值，设定步长、步数；

(6)对E求导，检测导数是否有零点，若存在零点，则零点对应的K值即为所求；若dE>0，则K值范围过大，取ΔK=ΔK/10，否则取ΔK=ΔK×10。返回步骤(5)继续计算，直到存在零点。

改进的K值自动估计算法，将传统算法应用其中，通过两次维纳滤波，首先对原始图像和噪声图像进行初步的估计，进而得到K值的大致取值范围，克服了因K值范围取值不当而造成估计不准确的缺点，利用此算法对K值进行估计准确度比较高。

将以上求出的点扩散函数和K值代入式 (4)，即可求得运动模糊复原图像。

4 实验研究

以运动模糊车牌[6]的复原为例，在摄像头拍摄时，因为车辆高速运动，加之曝光时间通常较短，得到的图像往往非常模糊，这就要首先做图像复原处理，最后得到一幅大致上比较清晰的图像以供后续处理。

图4为运动模糊车牌图像，用本文算法进行检测得出两幅图像的运动模糊参数分别为d1=13，θ1=8；d2=17，θ2=9。图5、图6分别为 K取经验值0.05和 K值自动估计得到的复原效果图。

从结果可以看出，利用本文提出的改进的K值自动估计算法与传统的算法相比,复原效果有明显的改善。该算法对于模糊程度未知、造成模糊的原因未知的模糊图像的复原问题具有重要的实际应用价值。

本文对运动模糊图像复原进行了研究，对运动模糊图像的退化模型、点扩散函数的求取以及维纳滤波K值的自动估计等几个问题给出了相应的改进算法。以运动模糊车牌复原为例进行了实验验证，并与传统的K取经验值进行了比较。实验结果表明，本算法能够较好地估计运动模糊参数，通过对方向微分算法的改进提高了运算速度，利用改进的K值自动估计对图像复原效果与传统算法相比较复原效果具有明显的改善。

[1]BEN E M,NAYAR S.Motion-based motion deblurring[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(6):689-698.

[2]CANNON M.Blind deconvolution of spatially invariant image blurs with phase[J].IEEE Transactions A cousfics Speech Signal Processing,1976,24:58-63.

[3]Sun Shaojie，Wu Qiong，Li Guohui.Image restoration for single blurred image[C].IEEE International Conference on Intelligent Computing and Intelligent Systems,2009:491-494.

[4]王晓红，赵荣椿.任意方向运动模糊的消除[J].中国图象图形学报，2000,5(6A):525-529.

[5]陈前荣，陆启生，成礼智.基于方向微分的运动模糊方向鉴别[J].中国图象图形学报，2005,10(5):590-595.

[6]Lin Hueiyung,Li Kunjhih,Chang Chiahong.Vehicle speed detection from a single motion blurred image[J].Image and Vision Computing,2008,26:1327-1337.