基于动态网格细分的烟雾模拟
王继州,袁雪霞
(1中原工学院 信息商务学院计科系,河南 郑州 450007;2.郑州经贸职业学院 计算机系,河南 郑州 450006)
在计算机图形学动画特效中,具有丰富细节流体(如烟雾或流水等)仍然是一个具有挑战性的任务,这是因为流体运动具有复杂性。现实的动画需要丰富的视觉细节 (如高分辨率的流体运动和烟雾现象)以及与环境的完美融合和高超的照明技术。然而现有方法的计算复杂度都非常高,目前所有GPU的流体模拟都依赖于纯粹的基于粒子模块化的方法(如粒子流体动力学或依赖规则网格模型),比较适合快速处理架构。规则网格的主要缺点是在空操作或无用操作上浪费时间。本文方法适用于计算机绘图中的实际视觉效果,研究重点集中于外观的表现上,而不考虑严格的物理正确性。
在计算流体力学方面,有自适应网格加密(AMR),如伯杰等[1]发展了一个基于图形上下文的自适应八叉树数据结构的离散化方法。另一种方式是纯粹的以流体模拟粒子为基础的类似于SPH[2]的方法。对GPU的流体模拟已有参考文献[3]和参考文献[4]的SPH方法。哈里斯等人[5]介绍了3D纹理,以模拟定期笛卡尔网格云动态。
本文将烟雾看做是特殊的流体,提出了一个解决方法,充分利用了硬件的具体性能优势,同时减少了复杂的层次遍历。流体数量极大地影响着整体性能,因此针对平流的速率存储和泊松求解的压力存储之间的不同,采用了不同的内存访问模式。
1 基于物理的流体模拟
1.1 流体动力学方程
物理模型上的无粘性、不可压缩的Navier-Stokes方程的质量和动量守恒方程式为:

该方程描述了液体流动的连续性,其中u表示该速度场,ρ表示密度,p表示压力场,f表示外力作用。
1.2 对流(平流)
动量方程已细分为一个平流过程和一个压力求解过程。使用从塞尔等人的改进麦科马克方法[6]进行误差补偿与校正。该方法可以简单地用在一个自适应网格上,只要确定了粒子轨迹的目的,三线性插值即可用于处理正确的边界。
1.3 离散的压强方程
采用洛萨索等与离散的分歧和一个八叉树数据结构的压力梯度方法,调用高斯散度定理的积分形式产生发散方差:

这里n是一个向外的单位法线,Aface是表面积单位,Vcell是体积单位。同样地,该定理是适用于压力的拉普拉斯算子,它实际上是一个div(grad(p))项:

剩余发散的压力梯度(▽p)最终通过一个对称矩阵实现。结果表明,梯度计算与应用的直接邻居网格单元作为扰动的压力位置,只要标准的核心差异在 O(Δx)内时,系统仍然能够得到一个一致的近似值。
图1显示了一个二维的例子。压力梯度大单元为:


图1 压力对八叉树的离散化
2 并行模拟
2.1 分解法
为了让并行处理在现代化的图像处理硬件问题中能够适当地分解,使用了一个具有43个细化的分层网格代替传统的具有23个细分的八叉树。通过这种方式更容易求解区域常数,另外,层次结构的深度通常比八叉树小,从而减少昂贵的内存遍历。
八叉树方案在实施时会遇到网格占用率不良的问题。例如,当被分配的一个线程块有8个节点或在一个复杂任务的分配方案中进行绘制曲线操作时,随着网格的逐步细化,64个线程块会被分配到一个单一亚网格里面。解决的办法是,对于每一个线程计算网格单元的中间值u*,把其平流速度和压力值p作为下一次的SIMD方式进行推测,结果,包含一个子网格的父网格也同时被模拟,这样就避免了复杂的分支操作。这样处理的时间花费只占总花费的1.5%左右。
2.2 平流运动的分层网格结构
麦科马克或半拉格朗日平流步法意味着对有效处理的分层网格系统的数据结构有几个要求。该主要操作是随机的,就像一个空间内读写访问局域网中的每个单元格周围目的地的粒子轨迹。二阶运算三线性插值的速度在任意的网格中都是一样的,计算速度比较均匀。这些观测值促使纹理存储读出速度快,因为读访问得益于和本地访问一样的纹理缓存速度;此外,纹理单元也支持快速三线性插值。
其基本思想是使用一个三维纹理容量的金字塔映射网格层次结构的内存。为了与一个三维贴图过滤形成对照,只有那些纹理元素在对应的单元格网域包含有效的当前模拟信息。图2所示为一个二维的分层网格例子,分层网格拥有一个交错安排和相应的纹理布局。除了3个速度分量,还有一个类型字段存储在Alpha通道,用以提供辅助信息的网格单元(如子网格的牵制或流入以及固体边界条件等)。

图2中,灰色纹理元素(实心箭头)代表实际网格,而条纹纹理元素(虚线箭头)描述父节点的平均值。在纹理金字塔内,活动网格块的安排被列在一个动态拓扑表中。这里有一行为每一个网格的第一个单元格分配相应的纹理块坐标和限定水平。网格拓扑完全依据此表定义,由CPU管理,其中也考虑到GPU分配任务线程纹理块。该网格分配给各个线程,通过阅读获得的纹理坐标表进入,通过增加ID线程作为补偿。图2中白色纹理的数字元素代表不使用内存开销,但允许在网络拓扑快速重排,在运行时分配内存。另外,它们中的一部分被用来正确处理插值以保持边界上的良好水平。
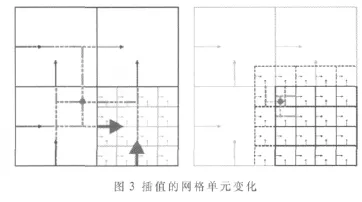
三线性插值需要附加的环境,一个网格单元不断变化的处理水平如图3所示。在粗糙细胞的情况下,所使用的平均速度来自黑色箭头的区域。通过这种方式,在粗略水平条件下进行插值就变得单一化。为了优化边界网格单元,分层更新是必要的。线程块粗格填充子细胞插值来自于黑色虚线表示的父细胞。这个过程允许使用的快速三线性插值在固有的纹理单元内,因为正确相邻关系在两个级别上都得到了保证。
2.3 压力分层网格的结构
以纹理为基础的数据存储的缺点是缺乏直接写访问,必须通过设备到设备复制整个网格的操作。在平流步骤,快速读取操作的优势缓解了这个问题。例如,联麦科马克与第二阶龙格-库塔方法意味着每个网格单元的总的读操作数为5,但是写操作数只有一个。在迭代求解器的情况下,写操作具有更多的权值。一个非自适应笛卡尔网格实验显示,基于纹理的方法显然慢于直接进入整体设备内存与联合读写的模式。
但是,为了实现高性能有几个限制必须保留,例如数据元素必须按顺序访问线程。由于这些限制的存在,压力值的存储与数组分层网格结构之间需要进行映射。数组分层网格结构的映射关系如图4所示。

图4中,除了在直接邻节点位置的细胞,矩阵中几乎一行中所有的元素都为零,典型的迭代求解器要求这些非零元素从内存读。对于恒定分辨率的块,压力值可以联合起来读到共享内存作进一步处理,但常规模式打破了边界的分辨率。为了减少过多的非联合访问,计算细胞的每个面的压力值(黑色)的方法通过存储放在一个额外的数组中进行。使用它们取代从细分细胞中读取压力值,此过程随着压力梯度的离散化而愈加完美。
2.4 动态网格细化
使用三种常见的标准来决定在下一时间步长中一个细胞是否精确而块是否粗造。在固体障碍下,当流体与物体相互作用时,网格足够精确地捕捉场景几何,分解视觉中的人工物体。第二个标准集中在高漩涡区域。当大小达到临界值的时候,网格是精确的。第三个规则细化网格在一个烟密度带内。下限不包括从高精度邻域中的非可见密度值,而对于非常密集地区的上限这是完全不透明的,只贡献了一些视觉细节。图5显示了漩涡跟踪动态网格细化的例子。

改进和粗化过程以并行方式运行,但是GPU本身不能管理自己的资源,数据必须被转移到CPU以管理网格。基于这个原因,每个线程块通知CPU带着与被细分的细胞或者被粗化的块的数据。有了这些数据,CPU能够在下一个时间步长中重组动态拓扑表以及给线程块分配任务。对约1283格的尺寸大的测量表明,与不需要这些传输的规则笛卡尔网格相比,作为结果的开销可以忽略不计(小于1%)。
3 模拟烟雾
运用集成可视化自适应流体模拟模块进行模拟应用。辐射度网格的射线追踪K对彼此平行的网格单元格中最明亮的光源,辐射度是阴影值的总和加上其余斑块的辐射度;密度和颜色值存储在一个额外3D纹理中供渲染使用;用标准的光线投射在GPU上的程序来呈现密度的三维体积和照明的信息。模拟的效果如图6所示。

本文采取了动态网格细分在平行的SIMD图形硬件上的流体模拟,减少了不规则的八叉树的执行情况,以适应硬件的性能限制。纳入辐射度为基础的可视化模块的模拟,取得了与烟一起互动的真实感渲染帧速率。与同等笛卡尔网格比较,开销是不可避免的,但如果改进的策略是精心挑选的,加速比是合理的。未来可以在多GPU系统上进一步扩展工作。
[1]LOSASSO F,GIBOU F,FEDKIW R.Simulating waterand smoke with an octree data structure[C].In SIGGRAPH′04:ACM SIGGRAPH 2004 Papers,New York,NY,USA,2004:457-462.
[2]MÜLLER M,CHARYPAR D,GROSS M.Particlebasedfluid simulation for interactive applications.In SCA′03:Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation,Aire-la-Ville,Switzerland,Switzerland,Eurographics Association,2003:154-159.
[3]KOLB A,CUNTZ N.Dynamic particle coupling forgpubased fluid simulation[C].Proc.18th Symposium on Simulation Technique,2005:722-727.
[4]ZHANG Y,SOLENTHALER B,PAJAROLA R.Adaptivesampling and rendering of fluids on the gpu.In Proceedings Symposium on Point-Based Graphics,2008:137-146.
[5]HARRIS M J,BAXTER W V,SCHEUERMANNT,et al.Simulation of cloud dynamics on graphicshardware.In HWWS′03:Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware,Airela Ville,Switzerland,Switzerland,Eurographics Association,2003:92-101.
[6]SELLE A,FEDKIW R,KIM B,LIU Y,et al.An unconditionally stable maccormack method[J].J.Sci.Comput,2008,35(2-3):350-371.

