数据融合技术在智能交通系统中的应用

陈 佳 ，闾立新

(1.江苏科技大学 电子信息学院，江苏 镇江212003；2.无锡科技职业学院 信息工程系，江苏 无锡214028)

21世纪以来，道路建设、机动车辆保有量均进入了快速发展的阶段，交通需求急速上升，交通问题呈现加重趋势，原有的单一依靠增加道路设施来满足需求的解决方案遇到了发展瓶颈。大家认识到，道路交通信息化的发展应与道路设施、道路交通的发展同步推进。应采用信息化手段支持道路建设、道路管理和交通管理，在增加道路设施的同时，通过道路信息化的手段来支持道路交通管理并提供道路交通信息服务，缓解道路交通问题。

智能交通系统ITS(Intelligent Transportation System)是在较完善的基础设施(包括道路、港口、机场和通信)之上，将先进的信息技术、通信技术、控制技术、传感器、计算机技术和系统综合技术有效地集成，并应用于地面运输系统，从而建立起大范围内发挥作用的、实时、准确、有效的运输系统[1]。从智能交通领域在世界范围内的发展现状和趋势来看，交通信息的采集、处理和分析已经日益成为交通研究和日常交通管理活动的重要组成部分。世界上很多大中城市的交通管理部门都已经拥有了实时采集、处理、分析和发布大范围道路网络交通信息的能力。

1 数据融合算法研究

数据融合（Data Fusion）也称作信息融合，是一个信息综合与处理的过程，一般的定义是：利用计算机技术对按时序获得的若干传感器的观测信息在一定准则下加以自动分析、综合以完成所需的决策和估计任务而进行的信息处理过程[2]。

数据融合作为一种数据综合和处理技术，涉及到了对ITS中多种交通信息采集装置和各种信息源的有效综合，包括共用数据的检测(获取)、过滤、相关分析、状态估计、目标识别和行为估计等，从而进行交通运行状态和环境判定、特殊事件判断等。ITS的数据融合分为两个层次：(1)低层处理，得到的是一些状态、特征和属性等，例如特殊事件的位置、属性；(2)高层处理，对应的是决策级融合，主要可以产生一些行动决策。

1.1 自适应加权数据融合算法

自适应加权数据融合算法是不等精度测量系统数据处理的一种重要估计算法。设有一个多传感器智能检测系统，有n个传感器对某一对象进行采样检测，如图 1所示[3]。

总均方误差为：

式(2)中σ2是各加权因子Wi的多元二次函数。根据多元函数求极值理论，可求得当加权因子为：

设每个传感器进行k次测量，式(1)中的X^可用k次测量的算术平均值进行估计，即

相应地，式(1)可写为：

综上，自适应加权融合算法的步骤是：(1)根据式(4)求出(k)；(2)求出；(3)根据式(3)求出最优加权因子 ；(4)根据式(5)计算出最优融合值。

1.2 基于灰色优势分析的数据融合算法

1.2.1 灰色绝对关联度

由灰色系统理论的绝对关联度定义和性质可知，灰色关联度的基本思想是根据曲线间相似程度来判断因素间的关联程度[4]。它对样本量的多少没有特殊要求，分析时也不需要典型的分布规律，因而具有十分广泛的工程应用价值。

定义 设序列 X0与 Xi长度相同，s0、si如上所示，则称：

为X0与Xi的灰色绝对关联度，简称绝对关联度。

此时的ε0i只与X0和Xi的几何形状有关，而与其空间相对位置无关。或者说，平移不改变绝对关联度的值。

1.2.2 改进的灰色绝对关联度

在某些实际工程应用中，有时仅考虑曲线间的相似性是远远不够的，还应考虑曲线间的接近程度。为此，在绝对关联度的定义中增加一个变量σs0i，σs0i反映了序列Xi在时间点上偏离X0的程度，引入σs0i后灰色绝对关联度ε0i不仅与 X0和 Xi的几何形状有关，而且还与 X0和Xi的接近程度有关[5]。

定义 设 X0=(x0(1)，x0(2)，… ，x0(n))为参考时间序列，Xi=(xi(1)，xi(2)，…，xi(n))为与之比较的时间序列，i=1，2，…，m，则称

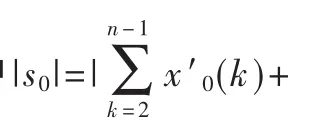
1.2.3 灰色优势分析

将改进的灰色绝对关联度应用在灰色优势分析的定义中，得出新的灰色优势分析的定义。

定义[6]假设γi为特征时间序列，Xj为与之比较的时间序列，εij(i=1，2，…，s；j=1，2，…，m)为γi与 Xj改进的灰色绝对关联度，则称

为改进的灰色关联矩阵。 对于式(2)，若δl≥δj，l，j∈{1，2，…，m}，l≠j，其中

则称时间序列 Xl准优于 Xj，记为：Xl>Xj。

若δl>δj， 则称时间序列 Xl优于Xj； 若对∀l，j∈{1，2， … ，m}，l≠j，恒有δl>δj， 则称 Xl为最优时间序列。

2 数据融合在智能交通中的应用及仿真结果分析

本系统主要用于交叉道口的车流量控制，设置在每个道路方向上的从机通过传感器采集到车流量信号后，将数据发送给主机，主机再综合各个方向的车流量信息后，决策并控制各道路方向的交通信号灯（红绿灯）的时间长短（不再是传统的定时控制）。主机将交通灯的控制命令及控制参数发送给从机，从机执行完交通灯的控制后立即又采集交通流量，如此循环下去，从而实现对道路交通的智能控制。

在数据融合的第一层采用自适应加权数据融合，第二层采用改进的灰色优势分析，每5组数据融合一次，执行的具体算法描述如下：

（1）由（5）式求出前 4组数据的加权平均值 y0(k)；

（2）将 r0=(y0(k-3)，y0(k-2)，y0(k-1)，y0(k))序列作为特征序列，由式(7)～(9)求得δj，j=1，2，3，4，5；

（3）求出δj，j=1，2，3，4 中最小的δx；若δx＜δ5，用第 5组数据代替第x组数据，输出前4组数据的加权平均值y0′(k)；否则输出 y0(k)。

本系统采用占有率、流量和速度3个参数作为拥挤自动判别的参数，以畅通、轻微拥挤、常发性拥挤、偶发性拥挤4种结果为例，每种结果仿真1 000次以观察算法的准确率，仿真结果如表1所示。

本文应用自适应加权数据融合以及改进的灰色优势分析，对机动车流量控制信息进行判别。实验结果表明，该方法判断准确率不低于96%，具有良好的识别性能，可利用这些检测结果对各个路口的交通灯进行实时控制，从而保证道路的畅通。

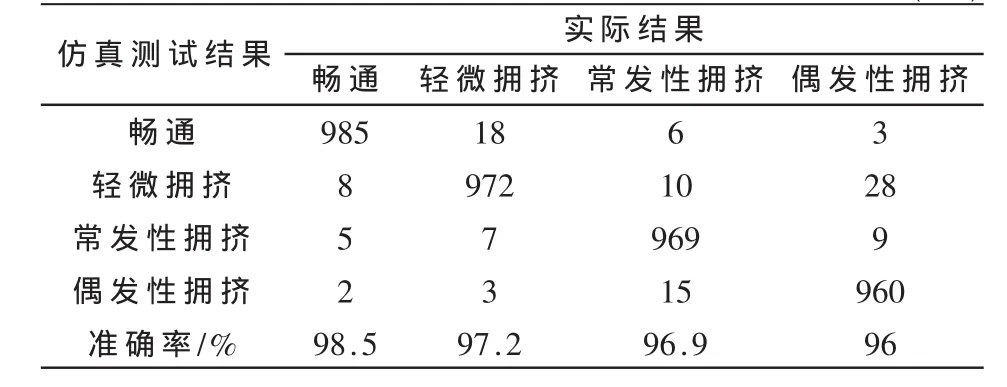
表1 交通流量验证结果(次)

[1]贺良华，侯晓东，于来宝.网络化信息采集在智能交通中的应用[J].控制系统，2008，4(3)：29-32.

[2]杨万海.多传感器数据融合及其应用[M].西安：西安电子科技大学出版社，2004.

[3]THAWORNWONG S，ENKE D.The adaptive selection of financial and economic variables for use with artificial neural networks[J].Neuorcomputing，2004(56)：205-232.

[4]刘思峰，郭天榜，党耀国，等.灰色系统理论及其应用[M].北京：科学出版社，1999.

[5]罗党.灰色决策问题的特征向量方法[J].系统工程理论与实践，2005，25(4)：54-58.

[6]唐汝桑，钱寒峰.智能交通信息采集中数据融合技术探讨[J].科技咨询导报，2009，28(4)：17-18.