工程计算巧用矢量正交分解法
何念民
(四川川投田湾河开发有限责任公司发电总厂,四川 石棉 625400)
工程计算巧用矢量正交分解法
何念民
(四川川投田湾河开发有限责任公司发电总厂,四川 石棉 625400)
将矢量定义引用到工程计算中进行运用,推论出机组最佳中心法,进而将最佳中心法推广运用到推力轴承加垫计算、轴心摆度中心轨迹计算等方面。
矢量定义;最佳中心法;推力轴承加调整垫计算;轴心摆度轨迹
0 引言
在数学中矢量的定义是既有大小又有方向的量;在物理学中既要由数值大小(包括有关的单位),又要由方向才能完全确定的量叫物理矢量,这些量之间的运算并不遵循一般的代数法则,而遵循特殊的运算法则,如矢量相加减遵循平行四边形法则、三角形法则、多边形法则等。常见矢量分析法就是正交分解法,正交分解就是将一个矢量按平行四边形法则把矢量分解到互相垂直的两个方向上,然后再求每个方向上的分矢量和,这样就把复杂的矢量运算转化成简单的代数运算。正交分解法的优越性就是方便求解不在一条直线上的多个共点矢量的和矢量。如图1,将矢量ri分解成了沿X轴方向的Xi和沿Y轴方向的Yi的两矢量。Xi、Yi遵循矢量运算法则,公式为:


图1 矢量正交分解图
1 巧用矢量正交分解推出机组最佳中心法
在水电机组安装工程中,经常会对机组进行中心测量和调整,常规方法就是在机组轴线位置测量圆周半径,进行中心调整。为更准确地进行中心调整,需要更多地对机组中心数据进行测量和分析,利用常规方法进行计算就难以处理和分析多组数据。这样我们就引用矢量正交分解法方便地对多组数据进行计算,然后根据计算结果对中心进行调整。其方法就是将机组中心各测点数据看成一个矢量,它们分布在同一个平面上,拥有共同的中心,我们可将其看做坐标系中心(0,0),然后对各测点矢量ri在正交坐标轴线X和Y上进行正交分解(如图1),再分别将各坐标轴上对应的分解矢量进行叠加。由于是进行中心调整,需要将叠加量除上一个n/2,得到一个新的坐标系,其圆心定为(X0,Y0),这个圆心就是机组的最佳中心,X0和Y0合矢量就是将要进行调整的中心量。最后计算出ri在新坐标系(X0,Y0)中的值ri′,将各ri′的值进行叠加取平均值,就得到图1中的圆即为最佳中心圆。所以最佳中心就是测量圆周各测点平均半径的中心,它与原测量圆周的中心存在一个位置偏差(X0,Y0)。根据图1中的矢量正交分解进行矢量运算,推出最佳中心公式:

最佳中心计算法在二滩、三峡等大型水电机组安装中已进行过成功运用。将其计算方法代入excel表格中进行公式运算,能快捷、简便、精确地进行数据计算和分析。
2 灯泡贯流式机组发电机推力轴承加调整垫计算的运用
在灯泡贯流式机组中(如图2),主轴由发电机导轴承(B1)和水轮机导轴承(B2)支撑,由于发电机转子的重量(W1)和水轮机转轮的重量(W2)横担在 B1、B2支撑点两边,则主轴会有一定的弯曲。为使发电机导轴承和主轴的接触面以及正反向推力轴承和镜板的接触面均匀接触,则须调整导轴承座与主轴的倾斜角一致,即在导轴承座后加调整垫片。在加调整垫过程中,需要测量的数据多,测量数据要求精确,所以工作量很大。为节省工作量,可利用最佳中心公式法计算求出各点数据。

图2 灯泡贯流式机组主轴承重支撑示图
首先在推力轴承座加垫均布位置测量8点数据,同时将某个点定为起始点。由于测量的是轴承座与镜板端面间的间距,可将间距值看成拥有共同中心(镜板面)的对称均匀分布的测点,然后利用最佳中心公式法计算轴承座端面本身的不平度。
例:某个电站轴承座与镜板间距内径千分尺表头读书为下表1,起始点角度为67.5°,点以顺时针为序,将各测点数据录入excel表格中进行公式运算结果见表1:

表1 未加垫测量值 单位:mm
从表1中两次均值可看出偏差很大,现将其进行矢量正交分解,利用最佳中心法在excel表格中对其进行公式运算,计算结果如表2。表2的结果虚拟了在这8个测点位置进行了加垫,计算出轴承座端面本身不平度为0.08mm,如在实际加垫时对加垫值进行适当的增减,紧固后其端面会有微量的弹性变形,则不平度将会变小。
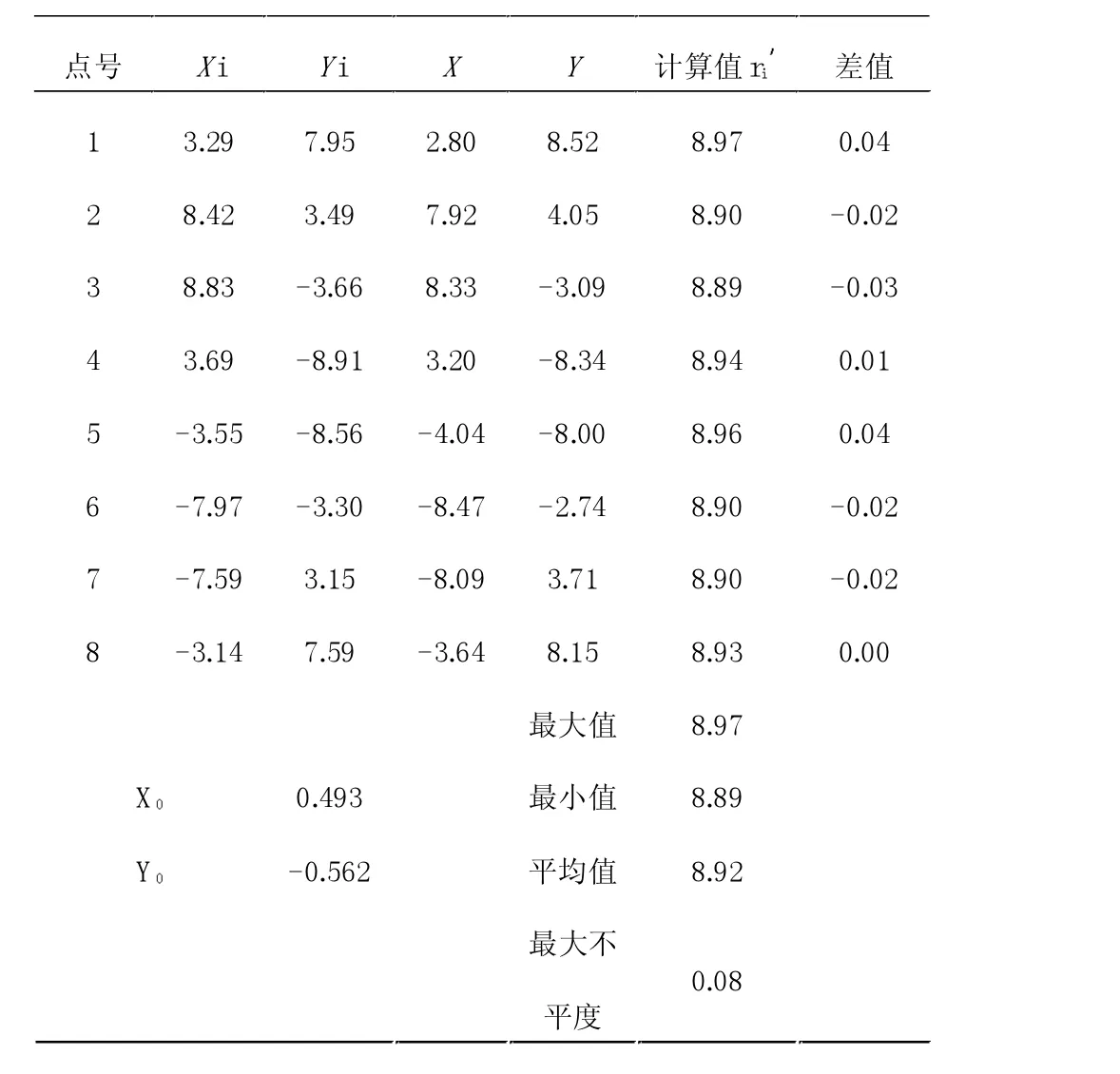
表2 计算加垫后各测点数据 单位:mm
从表2中得到计算平均值为8.92mm,可近似地将ri′看成一个半径为8.92mm的圆,现在需要求出在原坐标系(0,0)中各点的ri数值,点数为48个,1号测点位置不变,则可根据矢量坐标系列 方 程 式 为 (Ricosθi-X0)2+(Risinθi-Y0)2=R02。 R0为8.92,每个点在坐标系中(0,0)对应有角度,将R0、θi、X0、Y0数值代入公式,在 excel表格中进行公式运算,求出Ri的一个正根即为各点计算数值,其数据结果见表3。由于将间距假定为一个标准圆,所以计算出的Ri中对应原测点8点数据有细微的偏差,需要进行修正,尽量保证原始值。按照此加垫完成后理论间距表头读书应为8.18mm,设计要求此间距最大偏差为0.06mm,实际加垫完成后测量间距最大偏差为0.04mm,满足设计要求(计算加垫值以最小间距处进行计算,公式为δ2=δ0-11.00;δ1=Ri′-8.18-δ2)。

表3 计算值及其加垫值 单位:mm
3 机组轴线摆度轨迹的运用
在机组运行过程中,每道轴承处均安装有摆度测量装置,机组每旋转一周,测摆探头将测量出圆周各点摆度值,振摆分析仪将记录下这些值。如将机组静止时假定为0位,利用矢量正交分解法将各测点数据进行矢量分解,则可得到各点在每个轴线位置的矢量坐标,将各坐标点连接后就是机组轴心轨迹线。下表为某机组在某时刻某周期内8个均匀位置点的测量值以及根据这些测量值利用矢量正交分解法计算的坐标量和偏移中心量。

表4 机组轴心摆度分解坐标量及偏心单位:mm

图3 机组轴心摆度轨迹
4 结束语
在机电设备安装中,很多地方均可运用矢量正交分解法进行计算,不仅方便,而且快捷、准确、直观,如机组轴线调整、机组大型部件圆度、不平度计算等。本文仅在此做抛砖引玉,供读者朋友参考及借鉴,以便能在更广泛的领域进行研究运用。
Application of orthogonal decomposition method of vector in engineering calculation
HE Nian-min
(Sichuan Chuantou Energy Tianwanhe development Co., Ltd power plant,Shimian 625400, China)
Applies vector definition in engineering calculation, infers the optimum unit center method, then extends the method to other aspects such as the calculation of thrust bearing padding and axle centre throw orbit.
vector definition; optimum center method; thrust bearing padding calculation; axle centre throw orbit
TB113
A
1672-5387(2011)06-0067-03
2011-09-06
何念民(1974-),男,工程师,从事水电站水轮发电机组及辅助设备安装、调试、维护与检修等技术工作。

