可动心轨辙叉咽喉处结构优化对长心轨强度的影响

邹小魁，朱东方

(1.中铁山桥集团有限公司，河北秦皇岛 066205;2.陕西通宇公路研究所有限公司，西安 710075)

1 概述

随着铁路六次大提速工作顺利完成，提速前在正线站场咽喉区铺设了大量时速200 km的60 kg/m钢轨12号可动心轨辙叉单开道岔(产品图号:SC325)，该道岔在2001年完成设计、试制工作，并通过铁道部组织的验收审查。产品自上道以来，基本满足了铁路干线提速要求，提高了列车通过速度，满足了当时铁路建设的需要。文中所述除指明外，均指此道岔。

但受历史条件技术发展的局限，当时理论分析手段和试验条件还不够完善，因此，道岔设计受到了一定的制约。通过几年的运营实践，特别是货运方面提出了25 t轴重、时速120 km的要求，使得该型可动心轨单开道岔的不足也日益暴露，尤其是距长心轨尖端525～550 mm，断面宽36 mm处长心轨轨底部位是辙叉部分的薄弱点，由该处轨面所承受的弯矩、抗弯惯性矩和中性轴至轨底距离计算出的钢轨拉应力最大。加上轨底加工不良，纵断面变化急剧，心轨锻压段抗拉强度低于母材等因素造成局部应力集中，形成如图1所示，由轨底向上发展的疲劳裂纹断裂［1～3］。

图1 长心轨疲劳断裂

针对该型道岔长心轨尖端断面宽36 mm处疲劳裂纹断裂的问题，在保持长心轨结构尺寸不变的情况下，采取咽喉处局部结构优化的措施，以提高长心轨的强度，咽喉处可动心轨部分的平面结构如图2所示;同时采取瞬态动力学有限元理论分析长心轨尖端断面宽36 mm处的最大拉应力，以检验结构优化对提高长心轨强度的效果。

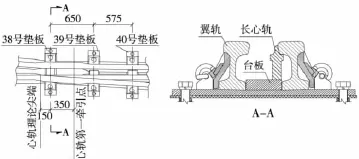
图2 咽喉处可动心轨部分平面结构(单位:mm)

2 瞬态动力学分析模型建立的方法

瞬态动力学分析是用于确定承受任意的随时间变化载荷结构的动力学响应的一种方法。可以用瞬态动力学分析确定结构在稳态载荷、瞬态载荷和简谐载荷的随意组合作用下的随时间变化的位移、应变、应力及力等。载荷和时间的相关性使得惯性力和阻尼作用比较重要。

2.1 有限元模型

为了简化分析，采用将长心轨简化为连续弹性离散点支承变截面梁;轨下系统支承简化为非线性弹簧支承;锥形车轮由翼轨滚向心轨时，因心轨逐渐支承车轮荷载，心轨所受轮载为一可变力，因此对心轨所承受荷载采用可变荷载来模拟。

2.2 模型的精确性

本文采用有限单元法求解长心轨断面宽36 mm处轨底拉应力，而断面平面几何惯性矩和中性轴至轨底距离不变，因此，求解长心轨断面宽36 mm处轨底拉应力则转化为求解长心轨断面宽36 mm处弯矩，以下简称长心轨弯矩。单元的细分程度决定了模型分析的精确度，单元越细，分析结果越准确。长心轨轨头横断面宽度斜率为1∶15，取5 mm长为一单梁单元，可分析到长心轨每一个断面的弯矩，满足精度要求。

3 计算结果及分析

3.1 既有道岔长心轨弯矩

时速200 km的60 kg/m钢轨12号可动心轨辙叉单开道岔，当货车以轴重25 t，时速120 km通过时，分析长心轨的弯矩。考虑速度效应及偏载效应［4］，轴重2倍的静轮载25 t为加载荷载;竖向弹性块的支撑刚度选用100 kN/mm。通过计算得到长心轨弯矩与时间的曲线如图3所示。

图3 既有道岔长心轨断面宽36 mm处弯矩与时间的曲线

由图3可知，轴重25 t的货车以时速120 km通过时，随着时间的增长，长心轨弯矩随着荷载从翼轨向心轨滚动过程中逐渐增大，当列车行至长心轨断面宽41 mm时(即列车到达距长心轨尖端627 mm处，以下长心轨断面宽41 mm位置均指此处)，时速200 km的60kg/m钢轨12号可动心轨辙叉单开道岔长心轨弯矩达到最大值13 522 N·m，当荷载通过长心轨轨头断面宽41 mm后，长心轨弯矩逐渐减小。由图3还可以看出，长心轨弯矩变化平稳，无突变现象。通过理论计算，在长心轨的弯矩最大时，长心轨轨底的拉应力为199 MPa，这与现场测试的长心轨应力相比较基本吻合。根据长心轨锻压段技术要求，心轨锻压段抗拉强度不低于母材抗拉强度的75%，材质为U75V的60AT钢轨屈服强度为880 MPa，考虑安全系数k为1.3，则钢轨的容许屈服强度为508 MPa，满足长心轨强度要求。但是，一方面由于心轨锻压的制造工艺、凸缘本身的截面变化和制造偏差在一定程度上影响了心轨的整体性能，使得长心轨的容许应力降低，另一方面由于现场可动心轨安装不到位，道床捣固没有达到设计要求等使得长心轨轨底拉应力经常表现为冲击应力，并且应力常常成倍增加。这些因素容易使长心轨产生由轨底向上发展的疲劳裂纹断裂。

3.2 调整岔枕间距对长心轨弯矩的影响

保持列车荷载、速度等参数不变，在满足电务转换要求前提下，岔枕间距由650 mm减小至600 mm，考察长心轨弯矩与时间的变化规律如图4所示。并且求解长心轨弯矩最大时的列车荷载作用点。

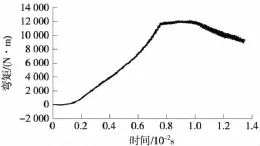
图4 岔枕间距对长心轨弯矩的影响

由图4可见，随着时间的增长，长心轨弯矩随着时间的增加而增加，以列车运行速度与时间为依据，计算得出当列车行至长心轨断面宽41 mm时，长心轨最大弯矩为12 067 N·m，当荷载通过长心轨轨头断面宽41 mm后，长心轨弯矩逐渐减小。当岔枕间距从650 mm减小至600 mm时，长心轨最大弯矩减小了10.8%，即最大拉应力减小幅度较大，可以有效延长长心轨的使用寿命。

3.3 弹性垫板对长心轨断面宽36 mm处弯矩的影响

由图2可知，可动心轨咽候处垫板结构为刚性结构(长心轨下的台板材料为45号钢)，因此长心轨轨下支承刚度较大，当车轮从翼轨向心轨的滚动中，由于长心轨受力较大，而且其断面较小，则受到的拉应力较大，容易产生疲劳断裂。弹性垫板是在台板下底板上采用橡胶硫化工艺，将橡胶与底板、台板硫化在一起，并且采用相关结构以保证台板与底板之间的连接牢固。对序号38至40号垫板采用弹性垫板，将进一步降低长心轨受力，并使可动心轨部分的刚度趋于均匀，以减小列车的动力作用和提高轨道的平顺性。

保持其他条件不变，将可动心轨部分38至40号刚性垫板改为弹性垫板，考察弹性垫板对长心轨弯矩的影响。通过计算可得弹性垫板对长心轨弯矩影响如图5所示。

由图5可知，长心轨弯矩呈上升趋势，列车荷载到达轨头宽41 mm断面时，弯矩达到最大10 247 N·m，而当列车通过41 mm断面之后，长心轨弯矩呈下降趋势。与未优化结构之前相比较，当采用弹性垫板之后，长心轨的最大弯矩由13 522 N·m减小至10 247 N·m，减小了24.2%。

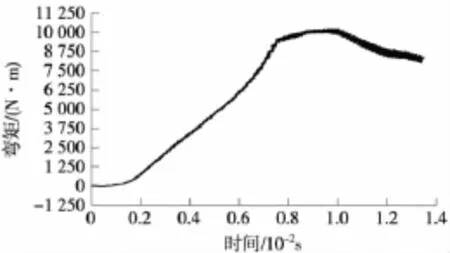
图5 弹性垫板对长心轨弯矩的影响

3.4 38号垫板台板高度降低2 mm对长心轨断面宽36 mm处弯矩的影响

对可动心轨部分第38号垫板台板降低2 mm，使得长心轨尖端部分悬空，以减小长心轨所受弯矩，考察台板降低2 mm对长心轨弯矩的影响如图6。

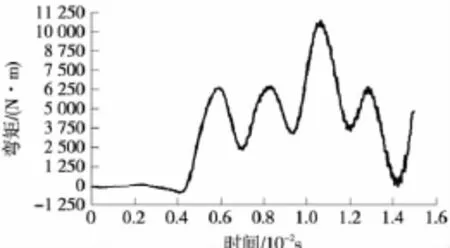
图6 降低台板高底2 mm对长心轨弯矩的影响

由图6可以看出，在长心轨轨头断面宽30 mm之前，长心轨弯矩基本不超过±300 N·m，可认为这一阶段，列车荷载全部由翼轨来承担。随着列车荷载的前移，长心轨开始承担列车荷载的作用，此时，长心轨前端与台板相接触，开始承受弯矩，并且所受弯矩逐渐增加，当列车行至长心轨断面宽43 mm处(即列车到达距长心轨尖端658 mm处)，弯矩达到最大值10 697.2 N·m。当列车通过心轨断面43 mm后，弯矩逐渐减小。与结构未优化前相比较，长心轨最大弯矩减小了20.8%。而且从图6可以看出，当38号垫板台板高度减小2 mm后，长心轨所受的弯矩波动较大，弯矩变化最大幅度为7 370 N·m，这说明长心轨此时有一定的振动，这将导致道岔咽喉部分不平顺性加大。

对于台板降低2 mm而使得道岔咽喉部分不平顺性加大，通过理论计算，列车在通过咽喉的过程中，轮轨的接触关系不发生变化，只是由于长心轨与翼轨之间所承受的列车荷载在发生变化，承受荷载的总体趋势为当列车由翼轨向心轨的转移运程中，翼轨所受列车荷载越来越小，心轨所承受的荷载越来越大，并且翼轨与心轨承受的荷载为交变荷载。取最不利状态，即由翼轨承担所有的列车荷载作用，而长心轨不承受荷载，计算可得翼轨的挠度最大为2.2 mm，根据时速200 km客运专线道岔直向平顺度要求钢轨挠度不大于3 mm的要求，可见列车在通过咽喉时的不平顺性满足设计要求。

对于由于列车荷载引起的长心轨振动，可对长心轨采取严格防跳措施来克服，一种方法是在翼轨压型段采用防跳台配合心轨来限制心轨上跳;另一种方法是在翼轨压型段之后采用防跳顶铁下压心轨轨肢来限制心轨的上跳。当长心轨的振动通过以上方法来约束后，采用降低台板高度的方法来减小长心轨的应力是一种行之有效的好方法。

4 运营实践

时速200 km的60 kg/m钢轨12号可动心轨辙叉单开道岔通过以上改进，已在京秦线上进行了30余组上道使用，运行至今，使用状况良好，运行平稳，该道岔整体强度加强，运行安全度提高，降低了道岔的故障率，减小了道岔养护维修工作量，受到了用户的肯定和欢迎。

5 结论

运用瞬态有限单元法和轨道动力学理论，分析了减小岔枕间距、采用弹性垫板和降低台板高度对长心轨弯矩的影响，计算结果表明:

(1)既有时速200 km的60 kg/m钢轨12号可动心轨辙叉单开道岔，在生产与制造达到设计要求和上道铺设运行后维护保养及时的状况下，长心轨强度满足使用要求;

(2)采用减小岔枕间距、弹性垫板和降低台板高度的方法都可以有效的降低长心轨的最大拉应力;当采用降低台板高度的方法时，应进一步加强长心轨的防跳措施和长心轨的跳动监控;

既有时速200 km的60 kg/m钢轨12号可动心轨辙叉单开道岔在铁路的六次大提速中起到关键作用，已经上道铺设2 000余组。在不对此道岔整体更换的前提下，可采用以上方法来提高长心轨的使用寿命。

由于可动心轨单开道岔消灭了辙叉的有害空间，进一步提高列车的运行速度、平稳性和安全性，减小轮轨相互作用，有效保护轨下基础，因此已经大量应用于既有线与新线的建设中。而深入研究其在列车荷载作用下的动力影响，对进一步提高铁路的运营速度和安全性将是十分有益的。

［1］岳国军，何耀民，于润学.SC325型道岔长心轨死角区的探伤方法［J］.京铁科技通讯太原刊，2004(4).

［2］闫海寿.SC325型可动心轨道岔尖轨的探伤方法［J］.铁道标准设计，2007(9).

［3］段剑峰.可动心轨道岔心轨轨断原因分析［J］.铁道标准设计，2009(5).

［4］陈小平.高速道岔轨道刚度理论及应用研究［D］.成都:西南交通大学，2008.