基于改进Canny算子与图像形态学融合的边缘检测方法

赵 洁,李 玮,郝志鹏,彭慧卿

(天津城市建设学院 电子与信息工程系,天津 300384)

边缘检测是图像分割、目标区域识别和特征提取等数字图像分析领域中的重要技术，目前已经成为机器视觉研究领域最活跃的热点课题之一。传统边缘检测方法包括Roberts算子、Sobel算子等一阶微分算子,以及Laplacian算子、LOG算子等二阶微分算子[1]。这类算法以满足一阶导数极大值点或者二阶导数过零点作为图像的候选边缘点，通过人为设定的全局阈值作为评价标准去除噪声与弱边缘点，将梯度值小于阈值的候选边缘点删除。由于微分运算对噪声比较敏感，抗噪声性能差，提取的边缘不够精细,因此在实际应用中受到了限制[2]。对于边缘检测算子性能优劣，Canny提出了三个评价准则[2]：高信噪比准则、定位精准准则和单一边缘唯一响应准则，并据此提出了Canny边缘检测算子。实际应用证明,Canny算子具有较好的边缘检测效果，因此迄今为止一直被广泛应用。

近年来，很多学者都提出了基于Canny算子的改进算法，但大多数都是针对如何解决自适应确定双阈值的问题[3-5]。传统Canny算法采用高斯滤波器消除图像噪声，不仅会造成图像的过度光滑，而且容易造成缓变边缘的丢失，这样会导致复杂图像的弱边缘无法检测。另外，传统Canny算子中梯度幅值的计算方法没有充分考虑到3×3邻域内周围像素对中心像素的影响。针对上述问题与不足，结合小波融合技术的优势，本文提出了一种基于改进Canny算子与图像形态学融合的边缘检测方法。仿真结果表明，该算法有效地提高了边缘检测的准确性和完整性。

图1 3×3窗口中的梯度算子

1 传统的Canny边缘检测算法

1.1 高斯平滑滤波

Canny算子首先采用二维高斯函数构造滤波器，分别按行和列对原始图像进行卷积运算,得到平滑图像I(x,y)：

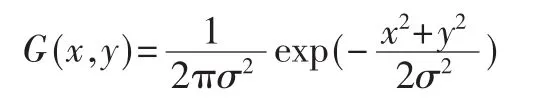
其中,σ为高斯函数的均方差，控制着平滑程度。

1.2 计算梯度的幅值和方向

Canny算法一般采用2×2邻域内一阶偏导的有限差分来近似计算平滑后的图像I(x,y)的梯度幅值和方向。x与y方向的偏导数阵列Px(i,j)和Py(i,j)分别为：

1.3 对梯度幅值的非极大值抑制

非极大值抑制的目的是找到I(x,y)中所有可能的边缘点，基本思想是使一个3×3邻域作用于梯度幅值阵列M(i,j)的所有点，如果邻域中心点的梯度幅值M(i,j)比沿梯度方向上的两个相邻点幅值大，则将当前的邻域中心点判别为可能的边缘点，否则将M(i,j)赋值为零，判别为非边缘点。

1.4 双阈值确定与边缘连接

Canny算子对非极大值抑制的子图像分别使用高低两个阈值 τh和 τl，且 τh≈2τl，从而得到两个阈值边缘图像Th(i,j)和Tl(i,j)。双阈值算法要在Th(i,j)中把边缘连接成轮廓，当到达轮廓的端点时，就在Tl(i,j)的8-邻域位置寻找可以连接到轮廓上的边缘，这样算法将不断地在Tl(i,j)中检测边缘，直到将Th(i,j)中所有的间隙连接起来。

2 改进的Canny算法

2.1 自适应中值滤波的图像平滑方法

中值滤波是一种非线性滤波方法，可以克服线性滤波器（如高斯滤波）给图像带来的边缘模糊，它能在滤除噪声的同时很好地保持图像边缘。本文采用的是自适应中值滤波方法，对于密度较大的脉冲噪声，它比传统的中值滤波方法更能有效地抑制滤波造成的边缘模糊问题，保护图像边缘细节。设fij为图像点(i,j)的灰度，Aij为中值滤波的当前工作窗口，fmin、fmax和 fmed分别为 Aij中的灰度最小值、最大值和中值，Amax为允许最大窗口。则自适应中值滤波算法的基本步骤如下[6]：

(1)若 fmin＜fmed＜fmax，则转至步骤(2)，否则增大窗口 Aij的尺寸。若Aij的尺寸小于Amax的尺寸，则重复步骤(1)，否则输出 fij；

(2)若 fmin＜fij＜fmax，则输 出 fij，否则输出 fmed。

2.2 改进的8-邻域梯度幅值计算方法

由于图像边缘可能以任意角度通过像素阵列，因此通过分别计算平滑后图像 I(x,y)的3×3窗口中心像素 x方向、45°方向、y方向、135°方向的一阶偏导数有限差分均值来确定像素点的梯度幅值，充分考虑到各个方向对中心点梯度幅值的影响，最大限度地减少误差。借鉴于Sobel算子，这4个方向上的梯度算子如图1所示，对离邻域中心点最近的像素进行了加权，增强了抑制噪声的效果。

3×3窗口中心像素点的梯度幅值 M(i,j)和梯度方向θ(i,j)的计算如下：

3 图像形态学边缘检测原理与算法

3.1 图像形态学基本运算

图像形态学的基本思想是利用一个具有一定形态的称为结构元素的“探针”收集图像的信息，当探针在图像中不断移动时，便可度量和提取图像中对应形状间的相互关系以达到图像分析和识别的目的[6]。图像形态学的基本运算包括灰度膨胀 f⊕b、灰度腐蚀 fΘb、灰度开运算 f οb和灰度闭运算 f·b。

3.2 形态学边缘检测算子

传统的形态学边缘检测算子的基本思想是对原始图像做形态学梯度处理，使输入图像灰度变化更加尖锐，进而检测到图像边缘。借助上述各种形态学基本运算，常用的形态学梯度MG具有以下几种表示形式：

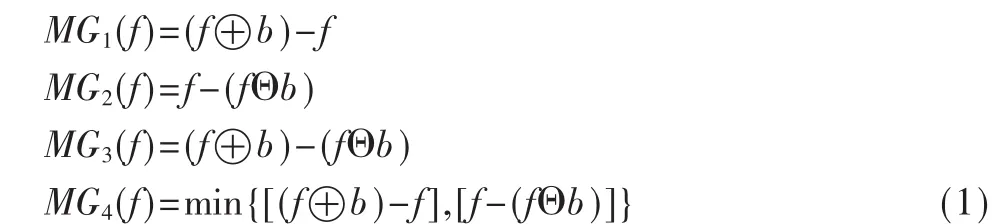
4 小波的融合技术

图像融合是将同一对象的两幅或更多幅图像合成为一幅图像，以获取对同一场景的更为精确、更为全面、更为可靠的图像描述。小波变换是图像的多尺度、多分辨率分解，它可以聚焦到图像的任意细节。基于小波变换的图像融合的基本原理如下[7-8]:如果一个图像进行L层小波分解，将得到(3L+1)层子带，其中包括低频的基带 Cj和 3L层的高频子带 Dh、Dv和 Dd。 用 f(x,y)代表原始图像，记为 C0，设尺度系数 Φ(x)和小波系数 ψ(x)对应的滤波器系数矩阵分别为H和G，则二维小波分解算法可以描述为：

其中,j表示分解层数；h、v、d分别表示水平、垂直、对角分量；HT和GT分别是H、G的共轭转置矩阵。小波的重构算法为：

5 基于图像融合的边缘检测方法

本文提出的基于图像融合的边缘检测算法流程如图2所示，具体实现过程如下：

(1)对采用改进的Canny算子进行边缘检测:①采用3×3窗口的自适应中值滤波进行图像平滑；②采用改进的8-邻域梯度幅值方法计算梯度的幅值和方向；③对梯度幅值应用非极大值抑制；④用双阈值算法检测和连接边缘。

(2)采用式 (1)的形态学边缘检测算子进行边缘检测，结构元素为半径为3的圆盘。

(3)将上述得到的两幅边缘图像应用小波的融合技术进行图像融合:①对两幅边缘图像进行三层二维DWT分解，得到图像的低频分量和高频分量；②取两幅图像的低频和高频分量的平均值进行融合；③经过小波逆变换重构融合后的边缘图像。

图2 本文算法流程图

6 实验结果及分析

实验所用PC机配置为：AMD Sempron 3200+CPU,1GB内存，集成显卡，仿真实验采用Matlab7.0编程。选取加入1%椒盐噪声的Lena灰度图像作为测试图像，分别用传统Canny算法和本文提出的融合算法进行边缘检测，实验结果如图3～图6所示，算法运算时间及相应参数如表1所示。

图3 含1%椒盐噪声Lena图像

图4 传统Canny算子检测结果

图5 改进的Canny算子检测结果

图6 改进Canny算子与图像形态学融合算法检测结果

表1 算法运算时间的比较

由图4、图 5比较可知，传统Canny算子对椒盐噪声非常敏感，而改进的Canny算子具有较强的噪声抑制能力，并且保持了Canny算子检测边缘清晰连贯的优势，兼顾了平滑噪声和抑制假边缘的需要；由图5、图6的检测结果比较可知，本文提出的融合算法丰富了部分灰度变化缓慢的局部边缘细节信息，具有更好的抗噪能力和细节保留能力，可以检测出比较完整并且连续的边缘，使边缘检测结果有明显改善。从表1的运算时间可知，本文算法与传统Canny算法的所需时间相当，在提高检测效果的同时没有明显降低检测效率。

本文结合小波融合技术的优势提出了一种基于改进Canny算子与图像形态学融合的边缘检测方法，仿真实验表明该算法检测提取的图像边缘包含了比原始图像更加丰富的边缘细节和更加完整的轮廓信息，提高了边缘定位的精度及准确度，兼顾了平滑噪声和抑制假边缘的需要，检测出的边缘连续性好，是一种有效的边缘检测方法。

[1]孙即祥.图像处理[M].北京：科学出版社，2005.

[2]CANNY J.A Computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intell-igence,1986,8(6):679-698.

[3]黄剑玲，邹辉.一种精确的自适应图像边缘提取方法[J]. 计算机工程与科学，2009，31(9)：53-55.

[4]雒涛.改进的自适应阈值Canny边缘检测[J].光电工程，2009,36(11)：106-111.

[5]王卫星.一种基于最大类间后验概率的Canny边缘检测算法[J].计算机应用,2009,29(4)：962-965.

[6]何明一，卫保国.数字图像处理[M].北京：科学出版社，2008.

[7]张德丰.MATLAB数字图像处理[M].北京：机械工业出版社，2009.

[8]陈浩，王延杰.基于小波变换的图像融合技术研究[J].微电子学与计算机，2010,27(5)：39-41.