有限元-边界法在光电目标散射计算中的应用

陈兆兵，郭 劲，林 森

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国人民解放军装甲兵技术学院，吉林长春130117）

有限元-边界法在光电目标散射计算中的应用

陈兆兵1，郭 劲1，林 森2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国人民解放军装甲兵技术学院，吉林长春130117）

为了解决三维目标电磁散射计算中准确性与有效性的矛盾，建立了有限元-边界法的计算模型，对三维腔体目标的电磁散射计算方法进行了研究。首先，分析了针对三维电磁腔体目标的电磁散射计算边界积分方法，引入了矢量格林函数，利用麦克斯韦方程得到电磁场形式与三维腔体形式的关系，建立了三维开口腔体边界模型；然后，结合光电目标曲面建模方法及高阶基函数的方法，建立了三维光电目标的有限元泛函，完成了有限元-边界法在三维腔体目标电磁散射计算中的应用；最后，进行了实例验证。分析显示，当三维腔体内部为空或为各向异性物质时，角度吻合非常理想，与传统模式匹配法所得结果的吻合度达90％以上。结果表明，采用本方法对三维腔体目标进行电磁散射计算，准确度、效率均有所提高。

光电目标；电磁散射；有限元；边界积分

1 引 言

三维光电复杂目标电磁散射的计算一直是某些工程应用中亟待解决的问题之一［1，2］。光电及电磁探测装备在现代战争中具有不可或缺的地位，及时有效地对来袭导弹、飞机等目标进行探测、识别与跟踪在未来战争中具有非常重要的意义。当前的飞行装置普遍采用隐身截面设计并覆有隐身涂层，隐身技术的应用给光电探测增添了难度，隐身飞机的特殊截面设计也使其被敌方有效探测的概率大大降低，如何有效计算这些复杂三维形体光电目标的电磁与光电散射截面已成为光电对抗及隐身与反隐身研究中的重要课题［3～6］。

电磁截面散射的计算主要有快速多极子方法，多层快速多极子方法，矩阵分解算法和阻抗矩阵小波稀疏化方法等［7～9］，这些算法在某种程度上满足了电磁截面计算的需要，然而随着隐身技术的进一步发展，这些算法却表现出极大的局限性。为了对隐身能力不断增强的当代飞行器进行有效的探测与识别，一些综合上述电磁散射截面计算方法的复合式方法相应问世，其中结合有限元方法与边界积分方法进行计算就是一个重要的研究方向。这种方法的原理是在所探测与计算的三维目标周围引入具有虚构性质的边界，其内部采用有限元方法进行计算，而外部则采用边界积分中的矩量法进行计算，边界两边的场通过场的连续性耦合，生成一个内部边界的耦合方程组［10，11］。以往的研究中有限元-边界方法主要用于求解外部场或无边界场的问题，用于光电目标中具有隐身特性的三维复杂目标的电磁散射的计算并不多见，且实际应用多集中于单一方法的运用［12～15］。本文以复杂三维目标的电磁散射计算为研究内容，以有限元-边界法为主要手段对复杂型三维腔体单元目标的电磁散射进行建模与计算，目的在于寻求一种求解效率高、求解精度好的复杂三维目标电磁散射计算方法。本文首先对腔体目标计算的一般方法与模型进行了探讨，然后应用该方法对某实例进行了计算，从而验证了理论的有效性。

2 电磁腔体有限元边界积分

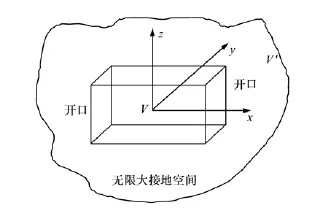
图1 三维开口腔体边界模型示意图Fig.1 Sketch map of three-dimensional boundary mode

三维电磁腔体目标的边界积分分析是目标散射分析与计算的前提。要对三维腔体目标进行精确的预估、电磁透射及耦合计算，首先需要对三维腔体目标进行合理的简化与模型描述，然后对模型进行分析与数学计算。在整个模型建立过程中三维腔体的内部场用矢量有限元变分方程来计算，而电磁腔体的外部场则以边界积分法来计算。在整个计算过程中，以有限元-边界方法对任意激励源作用下的无限大导电平面上的复杂三维开口腔体目标的散射进行了分析。图1表示复杂三维开口腔体目标的结构，图中的V假设为腔体内部空间，V′假设为腔体外部空间，该腔体为两端开口结构，其侧面为无限大的接地空间。

图1所示的三维腔体目标具有两端开口的性质，在电磁计算中要用到的介电常数有各向同性和各向异性之分。为了使计算模型具有一定的代表性，文中假设腔体内部的介质具有各向异性的特点，式（1）和式（2）分别为腔体内部介质的介电常数和相对磁导率的表达式。计算三维腔体外部无限大空间的电磁场需要满足一定的条件，其中最为重要的条件之一便是式（3）所示的矢量波动方程。

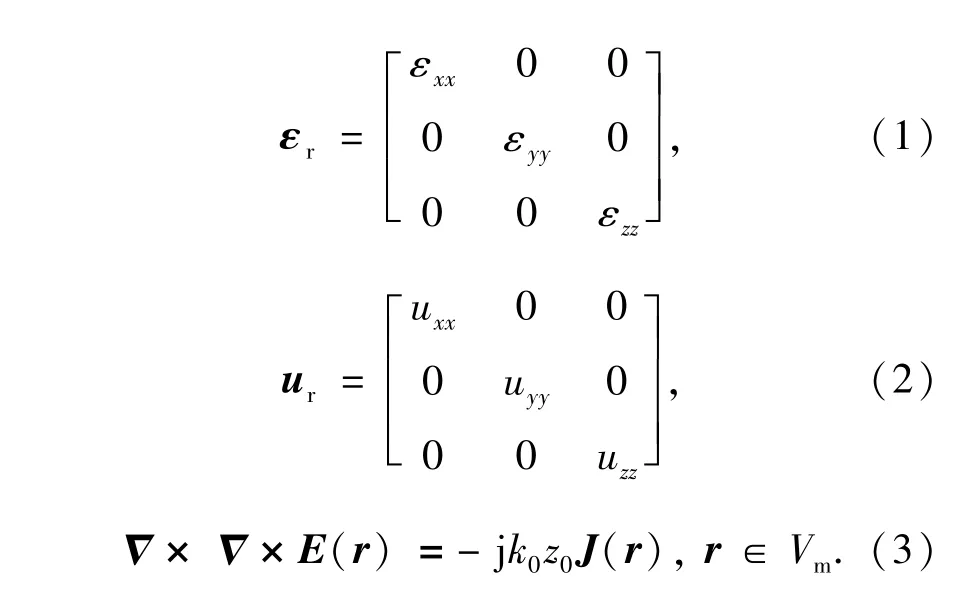
式中J（r）为作Δ用于腔体产生入射场的任意激励源，E为场强， 为旋度，κ0，z0为相应的系数。矢量格林函数是求解三维腔体电磁辐射的基本工具，在引入该函数的过程中需要注意该函数式必须满足一定的非齐次微分方程，本文将引入的矢量格林函数与式（3）进行点乘，同时在三维腔体的外部空间进行积分运算。而腔体的外部空间的场强函数表达式可以通过应用矢量格林函数恒等式来求解。在计算过程中，为了达到简化目标的目的，假设了场源被限制在有限的空间内，并且沿着半球面以及三维腔体中切向电场方向（除掉该腔体两开口以外）各个部分的积分均为零。在这种情况下，该类型的三维腔体的场强形式可以简化为式（4）所示的形式，该式中为典型半空间矢格林函数，s0为开口的平面区域。场强的最终形式可以通过将进行求解后带入式（4）来得到，将该场强的最终形式的函数式两侧分别取旋度，可以利用麦克斯韦方程得到电磁场形式与三维腔体形式的关系。而三维腔体开口处的电磁场求解是腔体目标电磁散射求解的关键之一，此处的电场与磁场关系可以通过将上述关系式进行z方向的取零准确获得，该关系式用式（5）表示。

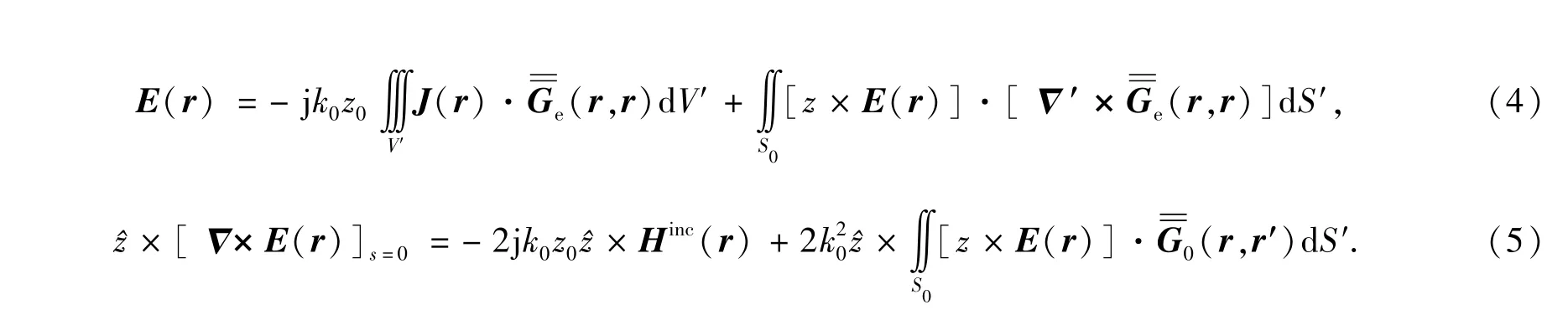
式中Hinc为入射磁场，V′为含有电流源J的积分区域，S为包围V′的面积。

3 三维目标有限元泛函建立

获得电磁场求解的基本公式后需要建立三维腔体目标的有限元泛函。在模型建立过程中，首先定义腔体内部为各向异性填充体；其次需要满足式（6）所示的波动方程。三维腔体电磁场计算的有限元边界条件有两个，分别为计算腔体内部电磁场的形式（如式（7）所示）和计算腔体两端开口处电磁场的形式（如式（8）所示）。

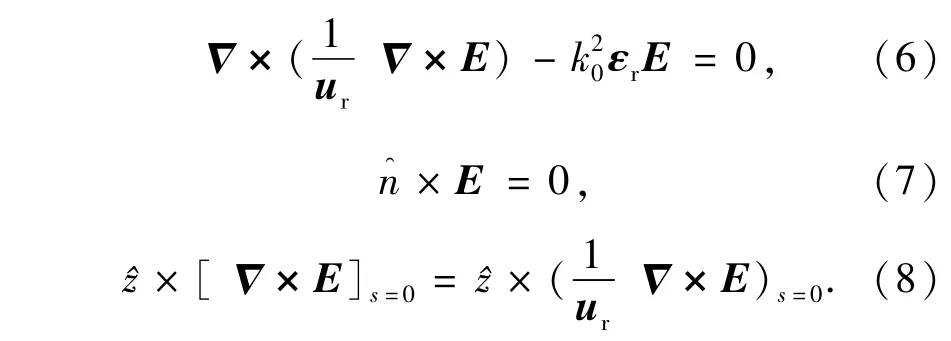
将式（5）代入式（8）可以获得三维腔体开口处电磁计算的有限元边界条件的精确表达式。依据变分不等式理论将上述式（6）～（8）进行变分。为了对泛函F进行离散，可以将腔体所在的区域分为M个六面体单元（非开口处），开口处剖分为Ms个矩形单元。这样可以得到总体的三维腔体目标电磁散射计算有限元泛函，如式（9）所示。对式（9）进行求和，并采用全局编号的形式代替上述建模中采用的局部棱边编号，进而得到式（10）所示的泛函简化式。

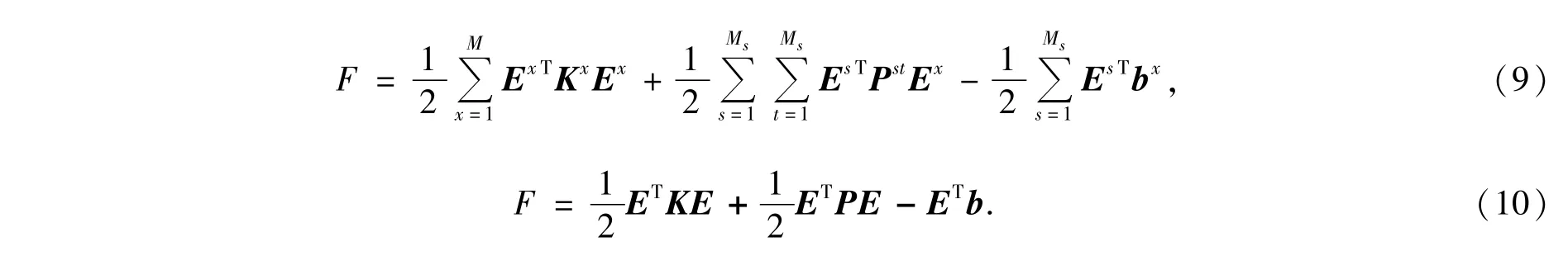
式中M为有限元单元函数，Ms为腔体开口部分三角形单元函数，κ是Ge在S0上的积分，P为稠密矩阵.

对原棱边的电场表示函数进行求导计算，并设其偏导数为零，便可得到三维腔体电磁散射计算有限元泛函的线性方程组，如式（11）所示，其中A=K+P。

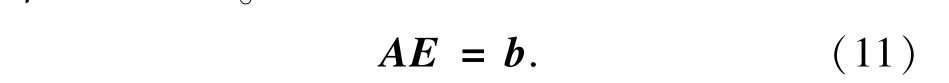
式（11）所示的线性方程组可以通过多波前法进行求解，从而得到上述形式的三维开口腔体的内部电磁场值，在求解过程中需要通过边界条件来限制，以保证使腔体内壁上的棱边场为零。这样就可以做到无论在何种激振源的激励下，三维腔体内部诸元素均可通过三点-高斯积分计算获得。

4 有限元-边界法的实例应用

针对上述形式的三维腔体目标的有限元泛函是否能精确计算其电磁散射进行了实例分析和实验验证，本文仅作实例仿真分析。在验证过程中，首先计算在平面波入射条件下三维开口腔体的雷达散射截面，同时计算产生入射场源离散射目标的距离能够在一个范围时该三维开口腔体的散射。为了进行对比，在验证过程中对腔体内部为空和腔体内部为各向异性材料两种情况下的电磁散射截面进行计算。三维腔体的结构尺寸为0.8λ×0.1λ×1.63λ（λ为激励源的工作波长）。三维腔体目标的电磁散射计算可以在上述两种情况下进行基于有限元-边界的应用性验证。

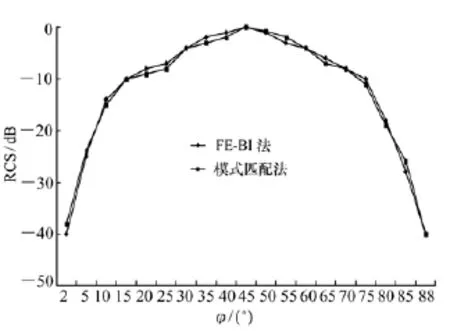
在验证过程中，首先对无限大接地矩形三维开口腔体的雷达散射截面（Radar Cross Section，RCS）随φ角的变化进行了分析，当腔体内部无填充物时，分析结果如图2所示；当腔体内部为各向异性介质时，对腔体RCS进行计算的结果如图3所示。在这种情况下，将入射平面波的θ角设为40°，腔体内部各向异性介质参数取式（12）所示情况。

?

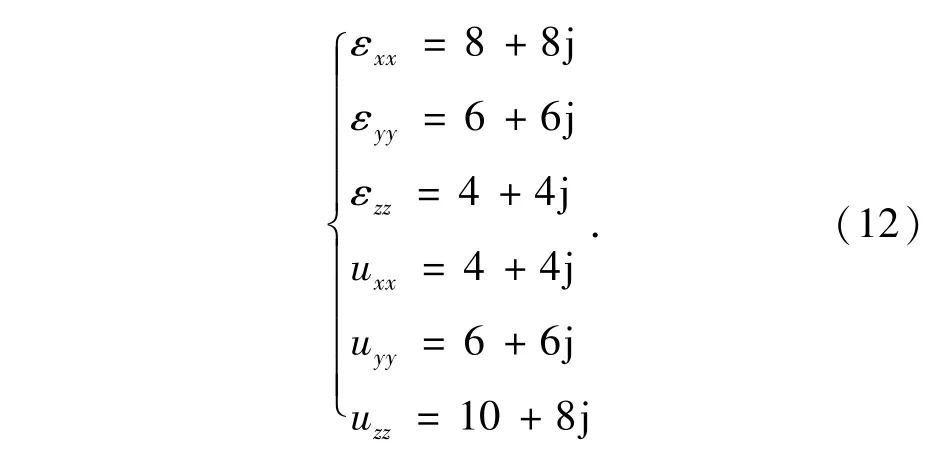
图2 腔体内部为空时RCS随φ角的变化

Fig.2 Change of RCS following φ when the dimensional bosom is empty

图2中当φ为0～90°时，按传统模式匹配法得到的计算结果与本文所探讨的有限元-边界法所计算得到的结果吻合程度较高，在一定程度上可认为有限元-边界方法在计算空腔电磁散射方面具有较高的精度。图3中显示的结果表明，当腔体中的物质为各向异性时，外部的雷达散射截面比图2中内腔为空时要小得多，而计算结果则有较高的准确性，本方法与模式匹配法得到的结果匹配重合度达90％以上。

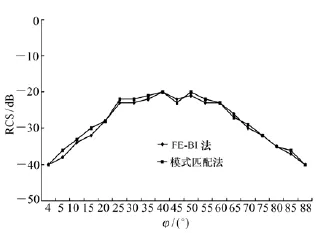
图3 腔体内部为各向异性物质时RCS随φ角的变化Fig.3 Change of RCS following φ when dimensional bosom is anisotropic matter

5 结 论

当前飞行器普遍采用隐身设计，其电磁散射较小时，会给探测告警增添极大难度。本文以有限元-边界法为计算方法对开口型三维腔体目标的电磁散射的计算方法进行了探讨。针对三维腔体的电磁散射，主要进行了有限元积分运算、有限元函数模型设计、腔体目标实例计算等。结果显示，有限元-边界法在计算三维腔体目标的电磁散射方面具有较高的精度。后续的工作中将围绕本方法的计算效率展开探讨。

［1］王长清，祝西里.电磁场计算中的时域有限差分法［M］.北京：北京大学出版社，1994.WANG CH Q，ZHU X L.The Finite-Difference Time-Domain Method on Electromagnetism Calculation［M］.Beijing：University Press，1994.（in Chinese）

［2］王永刚，孟艳丽，马文生，等.掠入射X射线散射法测量超光滑表面［J］.光学 精密工程，2010，18（1）：60-68.WANG Y G，MENG Y L，MA W SH，et al..Measurement of super-smooth surface by grazing X-ray scattering method［J］.Opt.Precision Eng.，2010，18（1）：60-68.（in Chinese）

［3］孟庆华，郭安儒，张勇杰，等.PS/PMMA复合材料的光散射［J］.光学 精密工程，2009，17（11）：2646-2650.MENG Q H，GUO A R，ZHANG Y J，et al..Light scattering property of PS/PMMA compounds［J］.Opt.Precision Eng.，2009，17（11）：2646-2650.（in Chinese）

［4］李萍，卢振武，夏利东，等.反射式内掩日冕仪的光学设计与杂散光分析［J］.中国光学与应用光学，2009，2（5）：408-413.LI P，LU ZH W，XIA L D，et al..Stray light analysis of internally occulted mirror coronagraph［J］.Chinese Opt.and Appl.Opt.，2009：2（5）：408-413.（in Chinese）

［5］郎治国，谭久斌.由相关函数拟合极值法提高位相板衍射光斑定位的计算效率［J］.光学 精密工程，2009，17（10）：2392-2400.LANG ZH G，TAN J B.Improvement of calculation efficiency for locating diffraction spot of phase plate with correlation function fitting extreme method［J］.Opt.Precision Eng.，2009，17（10）：2392-2400.（in Chinese）

［6］李大禹，胡立发，穆全全，等.CUDA架构下的液晶自适应波面数值解析［J］.光学精密工程，2010，18（4）：848-854.LI D Y，HU L F，MU Q Q，et al..Wavefront calculation of liquid crystal adaptive optics based on CUDA［J］.Opt.Precision Eng.，2010，18（4）：848-854.（in Chinese）

［7］聂小春，葛德彪，袁宁.边界积分法及连接算法分析任意腔体的散射［J］.微波学报，1999，15（4）：334-338.NIE X CH，GE D B，YUAN N.The analyze of dispersion of any cavity using boundary integral and connect arithmetic［J］.J.Microwaυes，1999，15（4）：334-338.（in Chinese）

［8］史林兴，王莉，李华，等.表面等离子体激元透镜设计及其数值计算［J］.光学 精密工程，2010，18（4）：831-835.SHI L X，WANG L，LI H，et al..Design and numerical simulation of plasmon polariton nanolens［J］.Opt.Precision Eng.，2010，18（4）：831-835.（in Chinese）

［9］张磊，何昕，魏仲慧，等.三角形星图识别算法的改进［J］.光学 精密工程，2010，18（2）：458-463. ZHANG L，HE X，WEI ZH H，et al..Modification of triangle identification algorithm［J］.Opt.Precision Eng.，2010，18（2）：458-463.（in Chinese）

［10］崔志伟，韩一平.电大尺寸开口腔体电磁散射的子结构法研究［J］.电波科学学报，2009，24（5）：914-919.CUI ZH W，HAN Y P.The substructure method for scattering by large open-ended cavities［J］.Chinese J Radio Sci.，2009，24（5）：914-919.（in Chinese）

［11］于旭东，张鹏飞，汤建勋，等.机抖激光陀螺温度场的有限元模拟与实验［J］.光学 精密工程，2010，18（4）：913-920.YU X D，ZHANG P F，TANG J X，et al..Finite element analysis and experiments of temperature fields of mechanically dithered ring laser gyroscopes［J］.Opt.Precision Eng.，2010，18（4）：913-920.（in Chinese）

［12］岳巾英，刘华，徐文斌，等.计算全息法测量长焦透镜面形和焦距［J］.中国光学与应用光学，2009，2（6）：502-507.YUE J Y，LIU H，XU W B，et al..Measurement of optical surface and foci of long focal length lens by CGH［J］.Chinese Opt.and Appl.Opt.，2009，2（6）：502-507.（in Chinese）

［13］贺俊，陈磊.使用红外干涉仪测量非球面面形［J］.光学 精密工程，2010，18（1）：69-74.HE J，CHEN L.Measurement of aspheric surfaces by infrared interferometer［J］.Opt.Precision Eng.，2010，18（1）：67-74.（in Chinese）

［14］林旭东，陈涛，明名，等.球面拼接镜的相对曲率半径测量［J］.光学 精密工程，2010，18（1）：75-82.LIN X D，CHEN T，MING M，et al..Measurement of relative curvature radius for spherical segmented mirrors［J］.Opt.Precision Eng.，2010，18（1）：75-82.（in Chinese）

［15］赵立荣，柳玉晗，朱玮，等.光电经纬仪单站空间余弦及多站面面交汇的飞机姿态测量［J］.光学 精密工程，2009，17（11）：2786-2793.ZHAO L R，LIU Y H，ZHU W，et al..Measurement of aircraft attitude by spatial cosine relationship in single-station and planes to intersection in multi-station of electro-optical theodolite［J］.Opt.Precision Eng.，2009，17（11）：2786-2793.（in Chinese）

Application of FE-BI to calculation of opto-electronic target scattering

CHEN Zhao-bing1，GUO Jin1，LIN Sen2

（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Armor Technique Institute of the People′s Liberation Army，Changchun 130117，China）

In order to solve the contradiction between veracity and validity for calculating the three-dimensional target electromagnetic scattering，a calculator mode about Finite Element-Boundary Integral（FE-BI）was set up to calculate the three-dimensional target electromagnetic scattering.Firstly，the three-dimensional target electromagnetic scattering calculation borderline integral was analyzed，and the vector Green function was introduced.On the basis of the connection between electromagnetism form and three-dimensional cavity form，the three-dimensional hatch cavity borderline mode was set up.Then，the finite element commonly function wasestablished by combining the optical target surface modeling method with the higher order function method，and the application of the FE-BI to calculating three-dimensional target electromagnetic scattering was achieved.Finally，the following example analysis was proved.It is shown that the angle tally is very ideal when the dimensional bosom is empty or anisotropic matter.The consistance has been 90％as compared with the traditional matching method.In conclusion，the veracity and validity of calculation are improved by the proposed method.

opto-electronic target；electromagnetic scattering；finite element；boundary integral

TN97；TP312

A

1674-2915（2011）02-0169-06

2010-11-11；

2011-02-13

陈兆兵（1980—），男，山东五莲人，博士，主要从事光电对抗装备的光机电结构一体化设计方面的研究。E-mail：chenzhaobing999@163.com