基于PCA故障重构的烟气轮机故障预测*

马洁 王秋燕 李钢

1 引言

大型旋转机械烟气轮机是炼油厂实现节能、减排和降耗的关键设备[1]。它将催化裂化过程中产生废烟气的压力能和热能经烟气轮机的膨胀做功转化为机械能，以驱动轴流式空气压缩机或给发电机提供动能，达到能量回收的目的。同时，烟气轮机的运行环境非常恶劣，转子磨损、催化剂粉尘堆积、壳体变形、仪表失灵等都有可能造成故障发生。以故障预测技术为基础的预测维修制度能够克服传统计划维修过剩的缺点，提高设备的利用率，减少维修费用，从而降低生产成本，提高企业的综合竞争力[2]。目前，旋转机械大部分故障预测方法都是假定故障是可以直接观测的，并且多采用单变量来预测，不能满足实际应用的需求。因此，采用基于故障重构的多变量故障预测方法，实现科学的预测维护，减少灾难性事故的发生，具有理论意义和应用价值[3]。

2 故障子空间与PCA模型

2.1 故障子空间

在多元统计过程监控 (Multivariate SPM,MSPM) 中，根据历史运行记录和工艺信息，当设备发生故障时，其故障形式如下[4,5]：

式中，x*表示对应于正常状态下的样本；x表示采样的故障数据；Ξ表示故障子空间（或故障方向矩阵）；f表示故障幅值。上述形式不仅可以表示单一故障，而且还包括了多维故障的情况。如果故障数据对于一类故障是可用的，Ξ可以直接从历史数据中提取出来。

2.2 PCA模型

主元分析(Principal Component Analysis，PCA)是把多个特征映射到少数几个综合特征的一种统计分析方法。假设 X ∈Rm表示一个具有m个测量变量的样本向量。样本矩阵 X ∈ Rn×m由n个样本组成，其中每一行对应于一个样本，每一列对应于一个测量变量的n次采样。PCA的基本原理就是采集处于正常操作条件下的过程数据，对其进行标准化处理，得到零均值且单位方差的 X ∈ Rn×m。然后进行主元分析，主元模型如下：

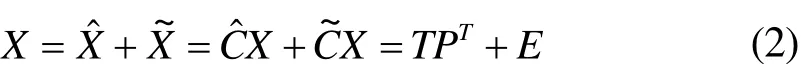
由上式可知，它将X分解成主元子空间(Principal Component Subspace, PCS)和残差子空间(Residual Subspace, RS)两部分[6]。X在PCS上的投影为：

X在RS上的投影为：

式中， T ∈ Rn×r和 P ∈ Rm×r分别是PCA的得分矩阵和负载矩阵，r表示选取的主元个数。投影矩阵Cˆ=PPT和= I-PPT。主元子空间主要反映正常数据变化的情况，残差子空间主要反映非正常数据变化的情况。当故障发生时，因受影响，RS上的投影将会显著增加。依据这个原理可以进行故障检测。子空间ˆS和S～互为交补空间，且

2.3 故障检测指标

在对过程性能进行监控时，一般是利用平方预测误差(Square Predicted Error，SPE)进行故障检测。s～空间中的SPE衡量了样本向量在残差子空间投影的变化[7]，即

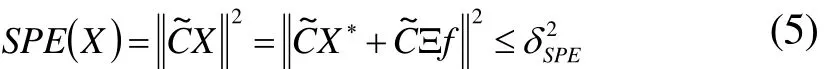
式中，SPEδ为SPE的控制限。在实际监测系统过程中，SPE优于其它检测指标。本文故障重构和故障预测都是建立在SPE的基础上。如果SPE满足上述条件，则认为过程处于正常工况。

3 基于故障重构的故障估计

故障幅值f无法直接测量，需要通过故障重构进行估计。故障重构的目标是通过消除故障的影响估计出名义上正常的样本数据x*，通过故障重构可以估计出故障幅值，从而采取相应有效的措施消除故障对生产过程的影响。故障估计就是将故障的幅值估计出来。针对一般的故障过程，Dunia等人提出了一种基于故障方向矩阵的过程故障重构方法，他们采用子空间的方法分析了残差子空间的故障可检测性、重构性、区分性，并给出了相应的充要条件[8]。类似Dunia等的思路，重构将沿着对应的故障子空间的方向往主元空间移动。即故障发生时的过程变量X的重构值Z为：

故障重构的目标是消除故障的影响，重构相应的系数向量，使重构后的SPE小于控制限[9]。

4 应用研究

4.1 烟气轮机故障检测

本文采用北京燕山石化公司烟气轮机组YT-7701A、YT-7701B、YT-7704A、YT-7704B四个通道传感器采集的隐含故障过程的振动烈度值，2005年烟气轮机原始振动烈度趋势曲线如图1所示。

图1 隐含故障过程的振动烈度曲线图

利用正常工况历史数据建立PCA模型，在此之前要对原始数据进行标准化处理，得到均值为0，方差为 1的数据矩阵X。本文采用累积方差贡献率(CPV)方法确定最优主元个数为 3，假设故障方向已经被提取出来[11]。如果重构的维数足够多，那么故障检测指标会回到正常范围内，即故障满足可完全重构的条件，并使该条件满足的最小故障方向维数，正是故障方向的维数，文中的故障方向矩阵维数为1。然后，对含有故障过程的数据采用SPE监测，如图2所示。

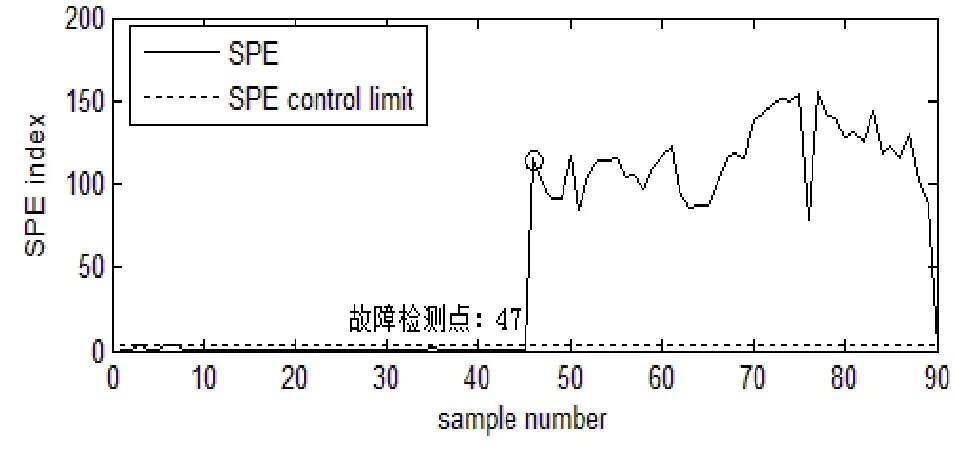
图2 利用SPE对烟气轮机进行故障检测

从图2中可以观察到故障在第47个样本点处被检测出来。在这里前45个是正常样本，其检测量均位于控制限下面。当故障被检测出来后，利用故障重构对故障向量kf进行估计，得到相应的故障幅值的估计值ˆkf，如图3所示。

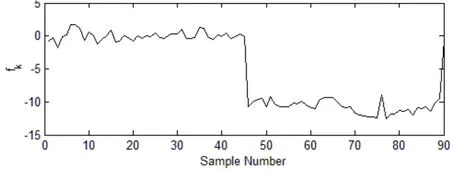
图3 故障幅值及其估计值

4.2 基于多层递阶方法的故障幅值预测

多层递阶方法把动态系统看成是非线性的、时变参数的系统，因而与烟气轮机的实际较为符合。为了验证上述方法的有效性，利用多层递阶方法对故障幅值ˆkf进行预测。

确定预测系统的数据模型如下[12]：

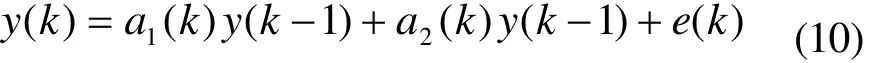
式中，y（k）表示第k个样本的故障幅值，a1( k)，a2(k )为时变参数， e ( k)为随机干扰造成的误差。利用推广的递推梯度算法，得出时变参数的估计公式：

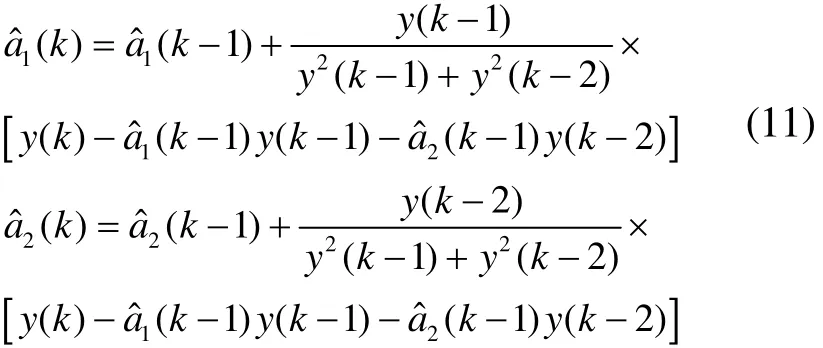
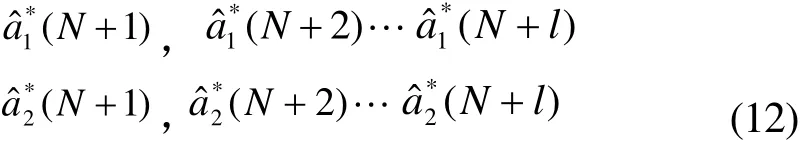
最后，得到 )(ky 的预测公式为：

选取 45=l ，采用基本多层递阶方法对后 45个样本进行预测，其预测结果如图4所示，其中实线代表实际值，虚线代表预测值。

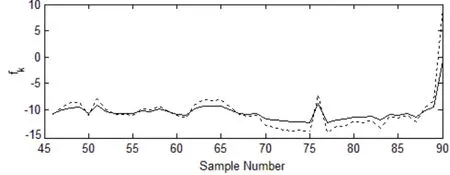
图4 基于多层递阶方法的故障幅值预测曲线

经计算可以看出，fk的绝对误差y - y ˆ=1.0230和相对误差，传统预测模型，例如自回归AR法相对误差一般都大于0.0400，而利用多层递阶方法预测的误差值较小，由此可见多层递阶方法对于烟气轮机的故障预报是有效的，而且预报精度比较理想。

5 结论

本文考虑了多变量的故障预测方法，利用故障子空间的概念，假设故障可完全重构，那么故障幅值就可以通过故障重构和多层递阶预测模型确定。故障重构技术充分考虑了过程变量在主元子空间和残差子空间的投影，当有故障发生时，残差子空间能够反映故障的变化情况，使其在减少数据维数的同时，保证了故障信息的有效性，为进一步的故障预测提供了可能。本文采用SPE作为故障检测指标对烟气轮机的故障进行了检测，并采用多层递阶方法对估计的故障幅值进行了预测，研究表明：基于PCA故障重构的方法适合于大型旋转机械烟气轮机的故障预测，并有较好的预测效果。

[1] 闻邦椿,武新华,丁千等著.故障旋转机械非线性动力学的理论与试验[M].北京:科学出版社,2004.

[2] 周东华,胡艳艳.动态系统的故障诊断技术[J].自动化学报,2009,35(6):748-755.

[3] 李刚,周东华.基于SPM的多变量连续过程在线故障预测方法[J].化工学报,2008,59(7):1829-1830.

[4] Gang Li, S. Joe Qin, Yindong Ji, Donghua Zhou.Reconstruction based fault prognosis for continuous processes. Control Engineering Practice,2010,18:1212-1213.

[5] 肖应旺,姚美银.基于主元子空间故障重构技术的故障诊断研究[J].计算机与应用化学,2008,25(1):93-94.

[6] Qin S J. Statistical process monintoring: basic and beyond.Journal of Chemometrics,2003,17:481-501.

[7] Ricardo Dunia, S. Joe Qin.A unified geometric approach to process and sensor fault identification and reconstruction:the unidimensional fault case. Computers Chem,1998,22:927-942.

[8] Dunia R,Qin S J.Subspace approach to multidimensional fault identification and reconstruction.AIChE Journal,1998,44(8):1817-1830.

[9] 李刚,秦泗钊,周东华.基于多尺度PCA的工业过程故障预测[J].华中科技大学学报（自然科学版）,2009,37:32-34.

[10] 王海清,蒋宁.主元空间中的故障重构方法研究[J].化工学报,2004,55(8):1291-1293.

[11] 李元,谢植,王纲.基于故障重构的PCA模型主元数的确定[J].东北大学学报（自然科学版）,2004,25(1):20-21.

[12] 韩志刚.多层递阶方法理论与应用进展[J].控制与决策,2001,16(2):20-42.