基于模糊神经网络的气流雾化染色机温度控制

周水英，蔡 杰，钟汉如

（华南理工大学 机械与汽车工程学院，广州 510641）

0 引言

染色工艺对温度控制要求非常严格, 染液的升温、保温和降温必须符合工艺要求, 否则将会产生色差、缸差、着色不匀等次品。染色过程的温度控制系统的设定值是由工艺决定的温度控制曲线,随着染液温度的变化，温度对象的特性也将随之改变。显然, 在某一给定值附近用传统的整定方法得到的PID控制器必然不能适应这种对象特性的变化，从而将得不到满意的控制效果[1]。

因而，本文针对染色过程温度控制系统的特殊性以及工业生产的实际需要，在分析温度对象特性的基础上，将神经网络和模糊控制相结合，取两者优点，以期达到良好的控制效果。

1 染色工艺过程

染色过程是一个比较复杂的物理化学作用的过程，一个完整的染色周期包括进布、漂白、染色、水洗、皂洗、软化和出布这七个过程。其中漂白、染色、水洗皂洗、软化的机械运动过程基本一致，不同之处在于温度和加入的助剂。气流雾化染色机在整个染色过程中，主要是控制染缸内染液执行一条温度按时间变化的工艺曲线。在工艺曲线中既有多段不同速率的升温段、降温段及多段不同时间的保温段，又有配料、加料、进水、排水等辅助工序[2]。图1所示是一个典型的分散-活性-浴法染色工艺温度控制曲线[3]。

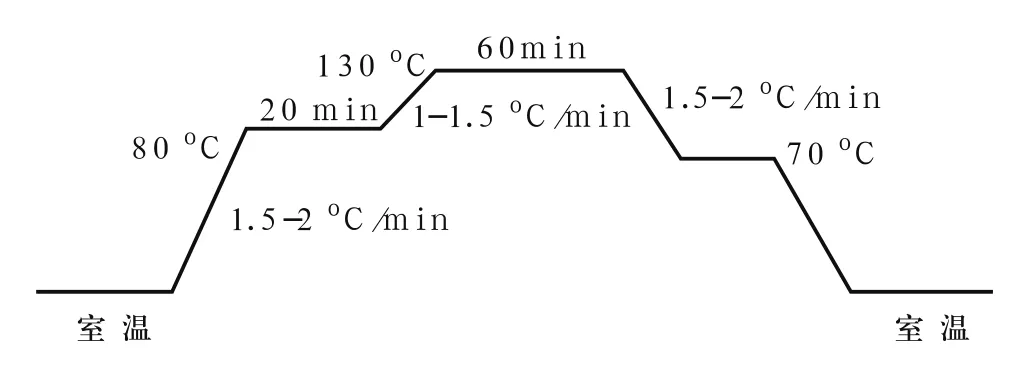
图1 分散-活性-浴法温度控制曲线

染色过程一般采用蒸汽加热升温，冷水冷却降温的热交换方式，蒸汽和冷却水的流量由电气调节阀控制，使染液温度严格按工艺要求变化。图1所示的这一温度曲线的实现过程是先从室温开始加热，升温的速率（斜率）是1.5-2℃/min，当温度上升到80℃时保持恒温20min，然后继续升温，升温速率为1-1.5℃/min,当温度上升到130℃时再持续60min。接下来再打开冷水阀，以1.5-2℃/min的速率降温降到70℃，维持10min,最后冷却至室温[4]。

2 模糊神经控制系统

2.1 模糊控制

模糊控制系统是以模糊数学的知识为基础，采用计算机控制技术构成的一种具有反馈功能的控制系统，模糊控制系统的基本结构与原理如图2所示,模糊控制系统一般由模糊控制器、输入输出接口装置、被控对象、执行机构和传感器等五个部分组成[5]，如图2所示。

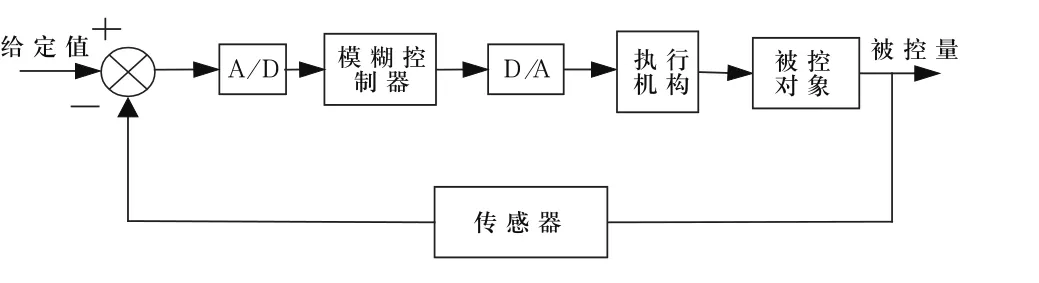
图2 模糊控制系统结构图

2.2 BP神经网络

BP网络是一种多层前馈型神经网络，其神经元的传递函数是S型函数，它可以实现从输入到输出的任意非线性映射。由于权值的调整采用反向传播(Back Propagation)学习算法，故而称其为BP网络。

BP学习算法步骤如下[6]：

1）设置初始权系数W(0)

它是较小的随机非零值。

2）给定输入/输出样本对，计算网络的输出

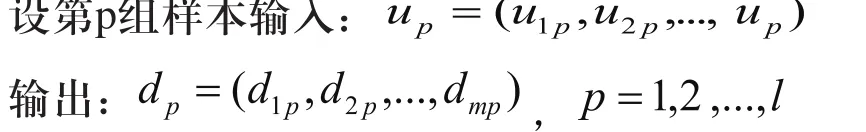
节点i在第p组样本输入时，输出为yip。

式中，Ijp是在第p组样本输入时，节点i的第j个输入。

可由输入层经隐层至输出层，求得网络输出层节点的输出。

3）计算网络的目标函数J

设Ep为在第p组样本输入时，网络的目标函数，取L2范数，则

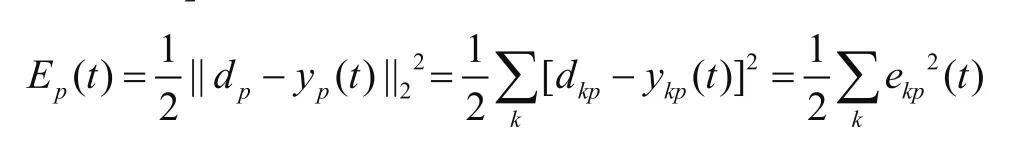
式中，ykp(t)是第p组样本输入时，经t次权值调整后网络的输出；k是输出层第k个节点。

网络的总目标函数：

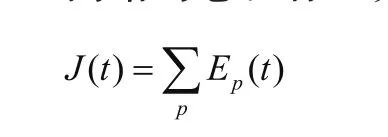
作为对网络学习状况的评价。

4）判别

若J(t)≤ε，算法结束；否则，至步骤5）。式中， ε是预先确定的，ε≥0。

5）反向传播计算

由输出层，依据J，按梯度下降法反向计算，可逐层调整权值。

3 模糊神经网络控制算法

本文将模糊控制和神经网络相结合，采用一个多层BP神经网络实现记忆模糊控制规则并进行模糊逻辑推理，将模糊逻辑控制表作为神经网络的学习样本，利用BP学习算法对网络进行离线训练，从而使用经过模糊控制集训后的BP网络实现染色温度的智能控制。

该控制方法中，BP网络输入层的节点分别对应于温度偏差和温度偏差的变化率的隶属函数中各个元素的隶属度[E(PB PM PS ZE NS NM NB)，Ec(PB PM PS ZE NS NM NB)]。

设温度偏差、温度偏差率和输出温度偏差的模糊语言变量分别为：TD(temperature deviation)、TDR（temperature deviation rate）和OUT-TD(outtemperature deviation)，它们的论域均为{ PB PM PS ZE NS NM NB}（PB—正大，PM—正中，PS—正小，ZO—零，NS—负小，NM—负中，NB—负大）。隶属函数的论域为：{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。

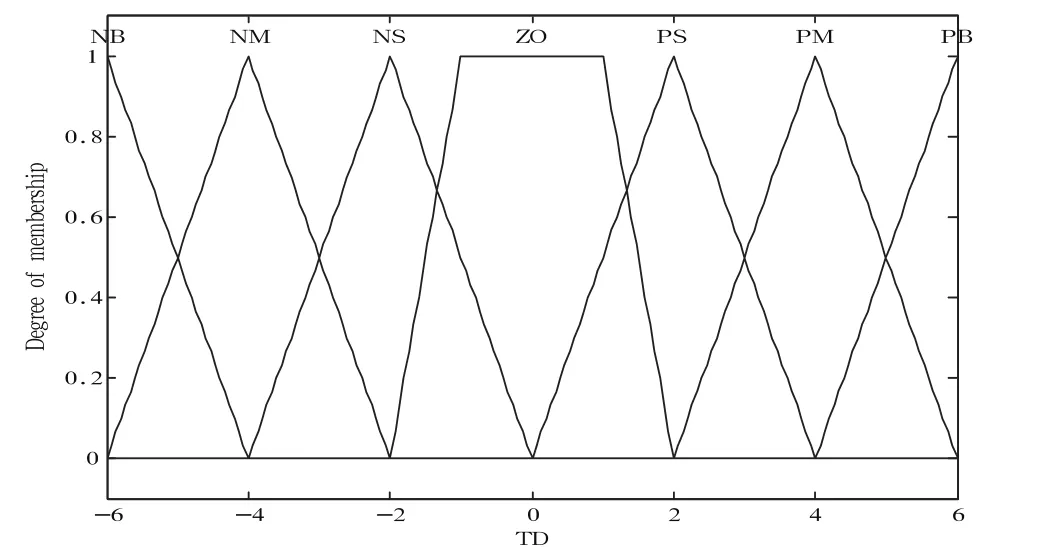
图3 输入量（温度偏差）隶属函数曲线

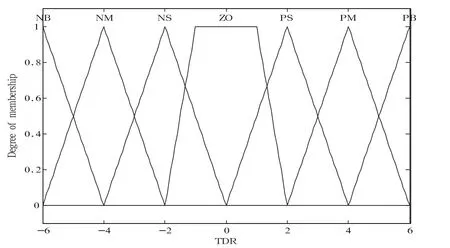
图4 输入量（温度偏差变化率）隶属函数曲线

控制的原则是：当误差E较大时，控制量U的变化应使误差E减小为目的；当误差E较小时，应该适量减小误差。例如：当误差为正大或者正中时，如果误差变化为正，说明误差正在不断增大，为了使误差迅速减少，应将控制量迅速减少，取负大。当误差E为正而误差变化EC为负，说明系统本身已经有减少误差的趋势，为尽快消除误差E 且又不超调，应取较小的控制量。例如：若误差为正大时误差的变化为负小，说明误差正在慢慢减小，应保持误差继续减小，控制量适当取负中；若此时误差变化为负中或负大时，说明误差正在快速减小，控制量不宜变化，取零[7]。

3.1 恒温控制

以温度偏差e和偏差变化率Δe作为输入，其论域范围是[-6，6]。根据e和Δe当前的值为依据来调整控制量。分别给e和Δe乘以0.6min/℃和6min/℃，将其处理为同意的论域元素。其隶属函数和模糊控制规则如表1所示。

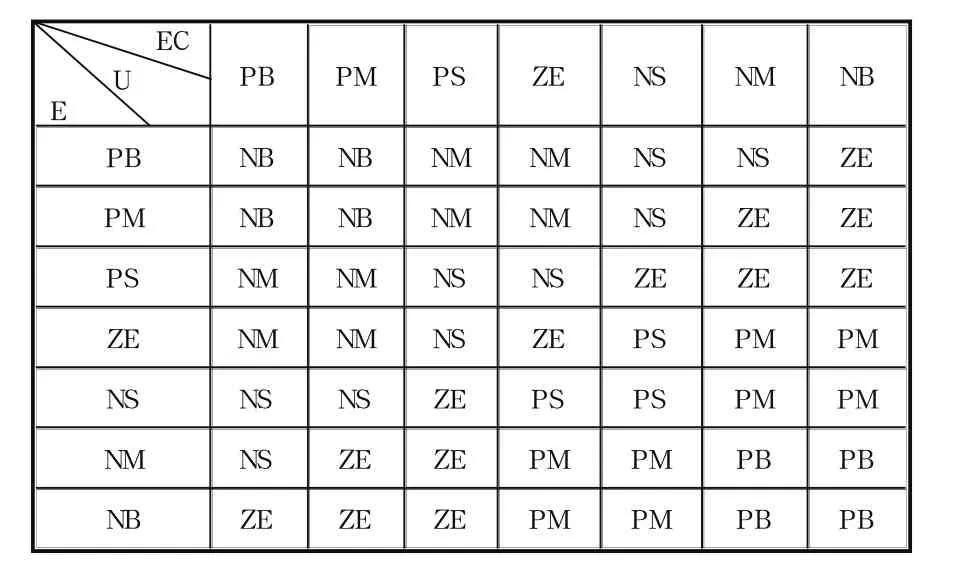
表1 恒温时的模糊规则表

利用模糊语言归纳手动制定控制策略 ，建立模糊控制器的控制规则。模糊条件语句所表示的控制规则如下(共有49条规则)：

由模糊推理得出控制量的隶属函数如图5所示。

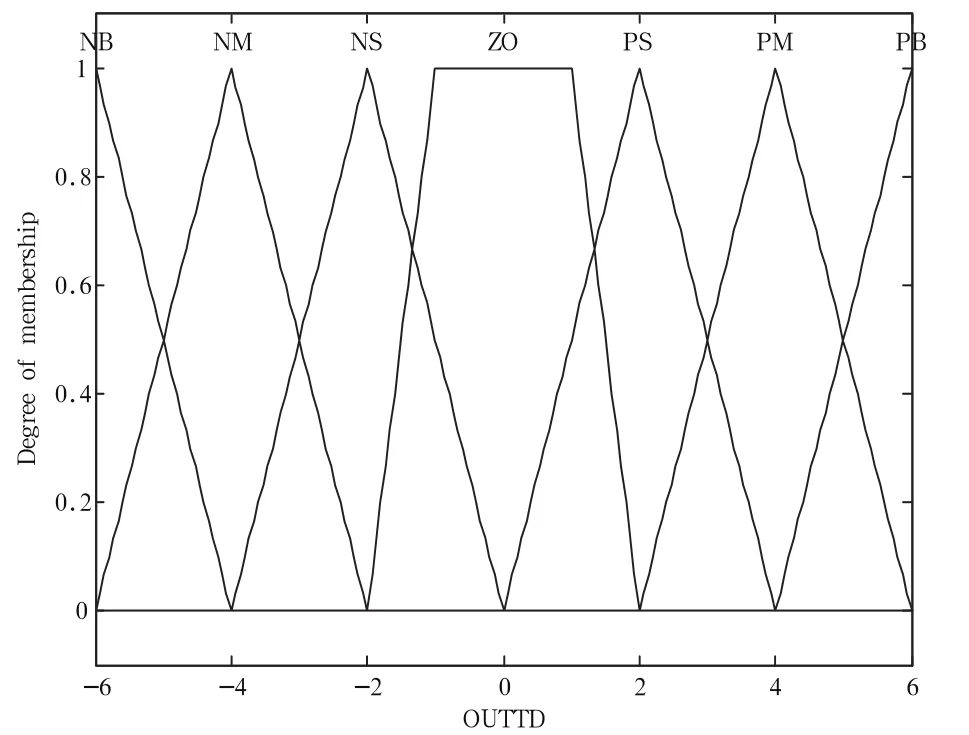
图5 输出量（控制量）隶属函数曲线

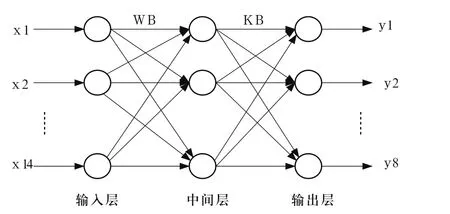
图6 温度偏差神经网络结构

这样就把控制规则转化为神经网络的输入输出，输入是TD和TDR，输出为U。令x1～x7为输入量温度偏差的模糊子集，x8～x14为输入量温度偏差变化率的模糊子集，y1～y8为输出控制量的模糊子集。由于控制规则表值有49条控制规则，每一条规则都是一对样本，共有49对样本。

3.2 仿真及结果分析

利用Matlab编写实现上述控制算法的程序，建立14个输入单元和8个输出单元的三层BP网络对数据进行训练，该神经网络结构图如图6所示。

选取不同的隐层结点数进行训练,并通过比较其相对误差的大小来确定神经网络的结构。选取的误差比较参数是均方差，均方差是各数据偏离平均数的距离（离均差）的平均数，均方差能反映一个数据集的离散程度，计算公式为：

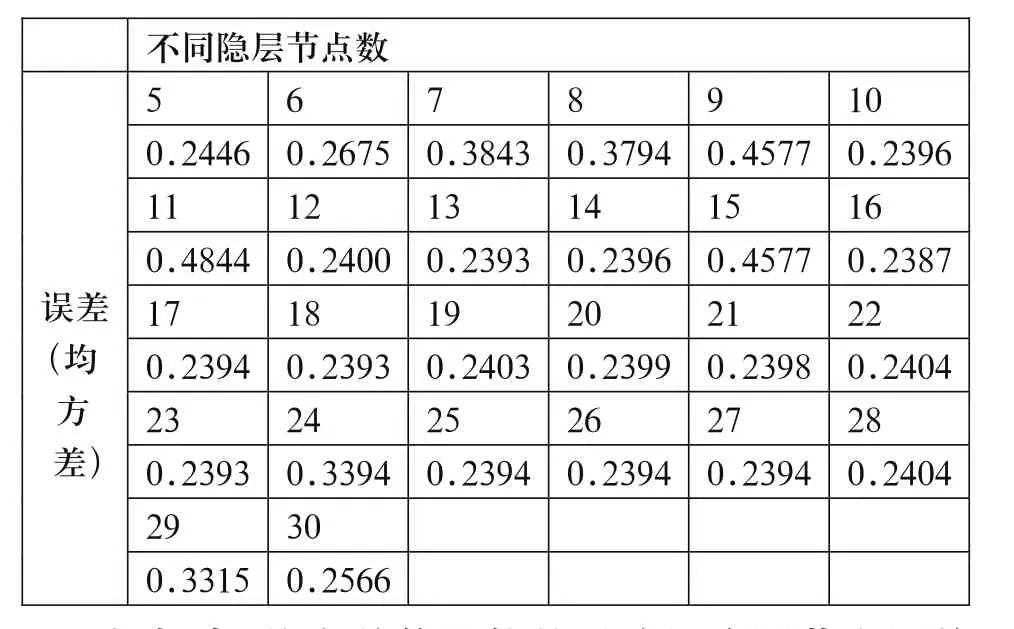
表2 隐层节点数与误差关系表

根据表2均方差的比较结果选择隐层节点层数为16，该神经网络经过65次训练后。目标误差达到要求如图7所示。

每一个训练点对应的径向误差如下图8所示，从该图可知，当隐层节点数为16，输出层节点数为13时，每个训练点的径向误差都比较小，最大不超过1.5%，可见预测效果较好。

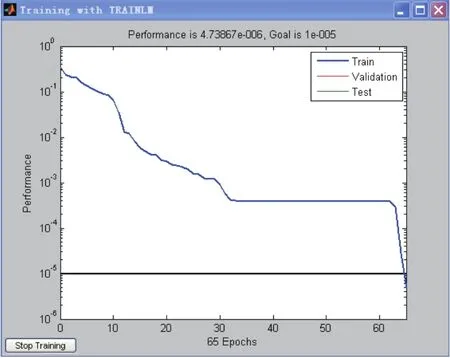
图7 训练过程图

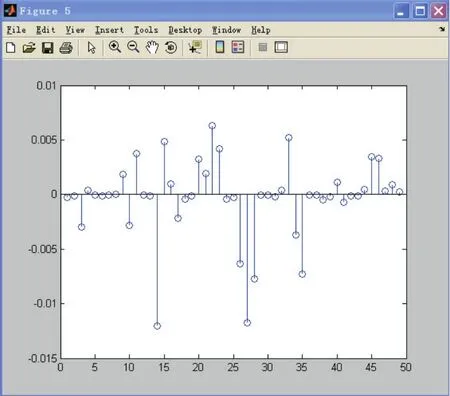
图8 训练点径向误差图

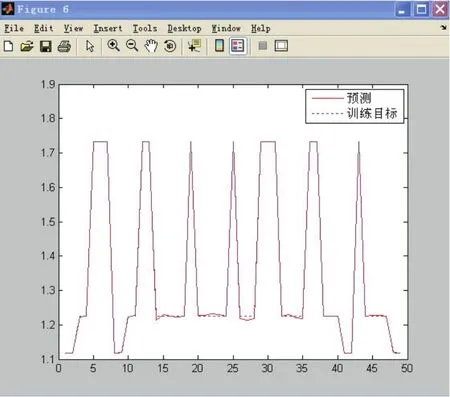
图9 预测曲线与目标曲线对比图

训练曲线与预测曲线对比如下图9所示，由该图可知，采用前面所述模糊推理规则和BP神经网络得到的预测结果曲线和目标曲线基本吻合，对温度达到了良好的控制效果。

以上是以恒温时采用模糊神经网络控制算法为例，分析了采用这种算法的具体思路和效果。升温过程和降温过程的思路与恒温过程大致相似，只需改变相应的隶属函数和模糊推理规则，同样可以得到较好的控制效果。

4 结论

本文所设计的控制算法是基于模糊神经网络的气流雾化染色机温度控制系统，该系统将人工智能中的神经网络控制技术和模糊控制技术相结合，采用闭环控制方式实现对染色过程中的温度的自动控制。其特点是：用神经网络代替传统的模糊控制器的隶属函数和权值，实现了模糊规则的自动更新。该控制系统对无法取得数学模型或数学模型相当粗糙的系统可以取得满意的控制效果；与传统的PID温度控制系统相比，该系统具有控制精度高、速度快,控制质量可靠、稳定等优点。

[1] 谢成祥,张健,邓志良.一种染色机温度控制器的设计[J].控制工程,2005,12(5):455-457.

[2] 陈立秋.染整工业自动化[M].北京:中国纺织出版社,2005.

[3] 郭清华,赵红英,袁利军.基于时间顺序控制的染色温度控制系统的实现[J].染整技术,2006,28(6).

[4] 上海印染工业行业协会.印染手册第2版[M].北京:中国纺织出版社,2001.

[5] 李士勇.模糊控制和智能控制理论与应用[M].哈尔滨:哈尔滨工业大学出版社,1990.

[6] 韩力群.人工神经网络教程[M].北京:北京邮电大学出版社,2006.

[7] 邓朝霞.电阻炉炉温模糊控制系统研究[J].机械与电气2006,(1):65-68.

[8] 飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社,2005.