基于粒子群算法的双工位切削参数优化

徐 剑，林献坤，韩世卓

（上海理工大学 机械工程学院，上海 200093）

0 引言

在现有的实际加工中，铣削用量的选择主要依赖于手册或经验，往往不能达到最优。一些多工位的专用机床的加工工艺不同于普通机床，直接应用手册将无法获取准确的加工参数。本文以双工位同时加工的钢轨整形机为实例，以切削手册的数学模型为基础，考虑加工中整形机的加工工艺和刀具的实际约束，建立了以最低能耗为优化目标的数学模型。并利用粒子群算法，对所建立的数学模型进行优化。

钢轨整形机由两把盘式铣刀组成，可同时对钢轨的踏面(S刀)和圆弧面(R刀)进行铣削。合理选择铣削参数对提高钢轨加工质量、降低能耗和提高刀具的使用寿命有着非常重要的意义。

1 切削参数数学模型

1.1 模型设计变量

切削三要素是指切削速度、进给量和切削深度。由于长钢轨加工时间长，往往需要一次成型，而且切削深度对刀具耐磨度的影响较切削速度和进给量要小，故视为已知量，不行进优化。实际生产加工中，较多使用主轴转速，在刀具确定的情况下，主轴转速与切削速度呈已知的线性关系，故选择主轴转速作为优化变量。整形机采用双刀盘双工位同时加工，考虑到钢轨的加工质量，要求两刀盘的铣削力大小相等，方向相反，故只要选择其中一把刀盘的转速作为优化变量即可，根据优化后的进给速度和刀盘参数即可计算出另一把刀的转速。根据现场实际加工经验，R轴切削量小，刀具寿命长，故选用钢轨踏面铣刀(S轴)转速为优化变量。

1.2 目标函数

长钢轨加工要求多工位同时加工，一次成型。优化的目标为能耗最低。同时给出在最优条件下两主轴的转速。

S刀盘切削力[1]：

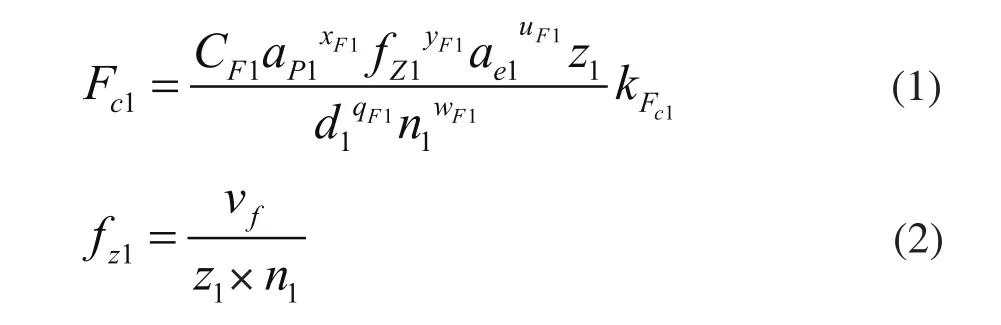
式中：αp1为铣削深度(mm)；fz1为每齿进给量(mm/z)；αe1为铣削宽度(mm)；z1为S刀盘的刀粒数；d1为S刀盘的直径(mm)；n1为S轴的转速(r/min)；vf为进给速度(mm/min)；CF1,xF1,yF1,uF1,wF1,qF1为铣削力系数；kFc1为切削条件改变时，切削力修正系数。

式中：vc1为铣削速度(m/min)。

R刀盘切削力：

1.3 约束条件

长钢轨加工时间长，中途不能换刀。受机床主轴转速、进给速度、刀具耐用度、工件质量等因素的影响，加工过程中设计变量(n1，vf)应满足如下约束条件：

式中：T1为刀具耐用度(min)；Cv1,qv1,xv1,yv1,uv1,pv1,m为刀具耐用度系数。kv1为切削条件改变时切削速度修正系数。

2 优化方法

2.1 粒子群算法概述

粒子群算法(particle swarm optimization, PSO)是由Kennedy和Eberhart 于1995年提出的，是一种基于迭代的优化工具，系统初始化为一组随机解，通过迭代搜索最优解。PSO先生成一群粒子，每个粒子都为优化问题的一个解，并由目标函数为之确定一个适应值。每个粒子将在解空间中运动，并由一个速度决定其方向和距离。通常粒子将追随当前的最优粒子而动，并经逐代搜索，最后得到最优解。在每一代中，粒子将跟踪两个极值，一个为粒子最优解，代表粒子自身的认知水平；另一个为全种群迄今找到的最优解，代表社会认知水平[2～5]。

式中：vi为粒子速度；xi为粒子解空间的位置；w为惯性权重，采用线性递减的策略，以平衡全局搜索和局部搜索能力[6]；C1，C2是学习因子，通常C1=C2=2；rand()是均匀分布在(0,1)之间的随机数；Pi为个体极值，即单个粒子从搜索初始到当前迭代对应的适应度最优的解；g为全局极值，是整个粒子种群从搜索开始到当前迭代对应的适应度最优的解；curCount为当前迭代的次数；loopCount为总的迭代次数。

图1 粒子群优化算法流程图

粒子群优化算法的流程图如图1所示。

2.2 适应度函数

3 实例

3.1 加工参数拟定

由国标 2585-2007，可知U74、U71Mn钢轨踏面稳定硬化区的表面硬度为HBW302～388(HRC32.5～42.0) ；刀具为硬质合金镶齿盘铣刀；加工时不用切削液。

表1 刀具参数

由切削用量手册[1]查得刀具系数，如表2所示。

表2 刀具系数

表3 刀工参数

3.2 优化结果及分析

采用MATLAB语言编写程序，粒子群算法中设定参数如下：群体大小为100，最大迭代次数设定为200，惩罚因子设为10。

表4 优化结果

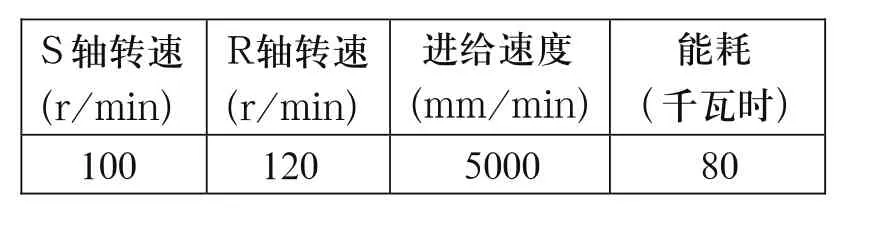
表5 工厂实际加工参数

4 结论

本文对长钢轨双工位整形机切削参数进行了研究，根据整形机的特殊加工工艺，建立了以最低能耗为优化目标，以机床的转速、进给速度、加工质量和刀具耐用度为约束的数学模型。并利用粒子群算法进行优化。对比现场经验参数获得的实际能耗，表明该方法优化的切削参数具有明显的节能效果。

[1] 艾兴,肖诗纲.切削用量简明手册[M].北京:机械工业出版社,1994.

[2] Kennedy J,Eberhart R C.Particle swarm optimization [A].Proceedings of IEEE International Conference on Neural Net2works [C].Piscataway,NJ:IEEE Press,1995.1942-1948.

[3] Eberhart R C,Kennedy J.A new optimizer using particle swarm theory [A].Proceedings of the Sixth International Symposium on Micro Machine and Human Science [C].Nagoya,Japan:IEEE Press,1995.39～43.

[4] Shi Y H,Eberhart RC.Parameter selection in particle swarm optimization.Proceedings of Annual Conference on Evolutionary Programming,San Diego,1998.

[5] 张丽平,俞欢军,陈德钊,胡上序.粒子群优化算法的分析与改进[J].信息与控制,2004,33(5):513-517.

[6] 陈贵敏,贾建援,韩琪.粒子群优化算法的惯性权重递减策略研究[J].西安交通大学学报, 2006,40(1):53-61.