一种降低OFDM系统峰均比的改进算法

高 天 ，李国民

(西安科技大学通信与信息工程学院，陕西西安 710054)

随着通信技术的发展，采用先进技术来有效利用频率资源成为一种必然要求。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术作为一种特殊的多载波传输技术，因其具有高速传输数据能力，高频谱利用率，抗多径干扰等优点被认为是第四代移动通信系统的核心技术之一，目前已广泛应用于HDSL、ADSL、DAB、HDTV、WLAN等领域中。

但由于OFDM信号是多个子载波信号的叠加，因此具有很高的峰均功率比PAPR(Peak-to-Average Power Ratio)，这就对发射机内放大器的线性特性提出了较高要求，如果放大器的动态范围不能满足信号的变化，则会带来信号畸变，使信号的频谱发生变化，从而导致各个子信道间的正交性遭到破坏，产生相互干扰，降低频谱效率，使系统性能恶化。国内外的学者专家对降低OFDM技术峰均比的方法做了大量深入研究，目前降低系统峰均比的方法大概分为3类:第一类是信号失真技术，包括限幅，峰值加窗[1]，峰值抵消等;第二类是编码类技术[2];第三类是概率类技术，典型的技术包括 SLM 技术[3]和 PTS技术[4]。这类技术是通过降低高PAPR序列出现的概率来降低系统的PAPR，因此，不会使信号产生失真。

1 OFDM系统的峰均比

图1是OFDM系统发送端的原理图，其中X表示IFFT之后的数据向量，向量中的元素X(k)，0≤k≤Nc-1。X(k)与s(n)的关系是

X是经过OFDM调制的序列，它经过数模变换、滤波放大等处理后得到OFDM系统的发送信号。接收端再进行相反的处理，通过FFT进行OFDM解调便可以恢复信息序列。

图1 OFDM系统发送端原理图

峰均比定义为[5]信号的峰值功率与平均功率的比值，一般用dB表示PARA的表达式

由式(3)可以看出，OFDM时域信号由N个子载波信号相加而成，这N个子载波由不同的调制符号独立调制。由于传送的数据是一个随机过程，在各个子载波上同时传输的数据是随机的。若所有子载波都被调制在同一个相位上，这时在OFDM信号上就会出现峰值，即在符号持续时间T内，能量集中在很小的时间段上，这就造成了OFDM符号有很高的峰均比。

对于包含N个子载波的OFDM信号，其PAPR的概率分布可以用累积分布函数(CDF，Cumulative Distribution Function)表示为

通常还可以从另一个角度来衡量OFDM系统的PAPR分布，即计算峰均比超过某一门限值z的概率，得到互补累积分布函数(CCDF，Complementary Cumulative Distribution Function)表示为

文中用CCDF来衡量OFDM系统内的PAPR分布。

2 SLM的基本原理

选择性映射方法的基本思想是通过引入小的冗余来提高峰均比的统计特性[6]。在SLM法中，发射机产生一系列不同候选信号的集合，这些信号表示相同信息，从中选择峰均比最小的集合来发射。但无论选择哪个集合都需发送边带信息，这样收方根据边带信息才能进行相应的反变换还原原始数据。因此它同时牺牲了部分发送带宽，增加了系统的计算复杂度以及系统硬件开销。但这种方法的优点是可以用于任意子载波数和调制方式，而且是非畸变地降低OFDM符号的峰均比。其原理框图如图2所示。

图2 SLM算法原理框图

从图2中可以看出，每实施一次SLM，就需要计算D个N点的IFFT变换，DN次复乘，因此，随着D的增大，使系统的计算量呈线性增长，如何降低SLM算法的复杂度是其是否可以得到应用的一个重要因素[7]。

3 改进的SLM算法

3.1 改进的SLM算法原理

如果可以在IFFT运算模块之前选择最优序列，就可以减少D-1组IFFT运算，从而大大减少SLM算法的复杂度。

因此，将SLM算法进行改进，让待映射的二进制比特序列B与M1，M2，…，MU异或，就得到B1，B2，…，BU这U个序列，他们代表相同的信息。这时通过判决算法选择最有可能具有很小PAPR值的最优序列BU进行传输，包括对BU进行映射，串并变换，IFFT以及后续相关处理[8]。可以看出改进后的SLM算法只需要一套IFFT，可以有效降低系统运行的复杂度，但降低了复杂度的SLM算法只是降低了高PAPR出现的概率，并没有完全有效地控制系统大峰值的出现。

打这天开始，阿巴常常跟着韩贝的船出海。阿巴的一切都好起来了，他不再孤独，不再把时间花在去沙滩画船了，他默写总拿满分，各门功课的成绩越来越好……

采用线性峰值抵消技术可以避免限幅滤波和峰值加窗技术对OFDM降低信号PAPR直接操作所带来的带外干扰，又可以进一步降低其PAPR。如果对上述降低了复杂度的SLM算法得到的信号进行峰值抵消，就可以更加有效降低系统的峰值功率比。因此将降低了复杂度的SLM算法与峰值抵消技术融合在一起，对SLM算法进行改进，将是一种非常有效地抑制PAPR的方法，其原理如图3所示。

图3 改进的SLM级联峰值抵消技术框图

3.2 SLM级联峰值抵消算法实现的两个关键内容

3.2.1 最佳序列的判决算法

最佳序列应该是随机性最好的序列，因此，本算法是对B1，B2，…，BU的随机性评判来选择最优序列。二进制 b it序列 B 在下列两种情况下得到的OFDM符号具有较高峰均比:(1)B中0和1的比例不等，即会出现长连0或连1的情况下;(2)当B是短周期的序列，如序列110011001100…。当这样的序列同M序列进行异或后得到的序列便是随机性较好的序列。这样序列的频谱也比较平坦，从而得到的OFDM符号也具有较低的峰均比[9]。因为B本身可能是随机性较好的序列，所以序列M1，M2，…，MU的取值遵循这样的原则:M1为全零序列，即对输入序列不进行加扰，M2，M3，…，MU选择不相关的m序列。

观察随机序列发现这些序列中0，1个数近似相等的序列即是要找的最优序列。频数检验[10]是最基本的检验一个位序列中0和1的个数是否相等。具体的方法是:对于0，1二进制序列b=b1，b2，…，bn定义Sn=(2b1-1)+(2b2-1)+…+(2bn-1)，可以看出当Sn为一负整数时，它表示序列b中0比1多的个数;当Sn为一正整数时，表示1比0多的个数。当越小，表明序列0和1的个数接近，这样的序列越有可能具有好的随机性，所以要选择的序列应该具有很小的可以将作为判决标准。

3.2.2 峰值抵消的实现

经过上述SLM算法，最优序列经过映射，串并变换，IFFT得到OFDM信号xm，这时xm出现高峰均比的概率已经大大低，但为进一步降低系统的PAPR，采用将其级联峰值抵消技术。

峰值抵消技术的基本思想是从信号中减去一个时延的一定幅度的参考函数，使得每个被减的参考函数至少降低信号的一个峰值样点[11]。sinc函数就是一个比较合适的参考函数。该函数的不足之处是它具有无限的响应，因此在实际应用中，应采取某种方法对其截短限时。把它乘以一个窗函数，比如升余弦窗，这样就不会带来不希望的带外干扰。图4为峰值抵消单元结构原理。

图4 峰值抵消单元结构原理

将SLM算法后的输出信号y首先进行峰值检测，提取出峰值特征参数[12-13]，峰值抵消脉冲发生器产生抵消脉冲，抵消信号的幅度可由非线性功率放大器特性决定。采用抽样信号作为抵消脉冲，抵消后的输出信号可以表示为

其中，Ki，φi，τi分别表示 S LM-OFDM 后修正第 i个信号峰值所用的幅度、相位和时延

其中，yth为设定的峰值门限。

文献[12]指出，采用限幅技术可以使系统功率谱带外辐射增加，但在采用同等程度的峰值抵消技术后，与原信号相比，信号的功率谱特性几乎未发生改变，没有产生较大的带外辐射。

4 仿真与结果分析

文中利用仿真手段对SLM级联峰值抵消算法的PAPR性能和在AWGN信道下OFDM系统误码率性能进行了分析，基于系统性能和复杂度的折衷，系统仿真参数为:子载波数 N=128，系统调制方法为BPSK，IFFT点数512;SLM算法中，U=4，M1取全0序列，图5为该算法流程图。

图5 SLM级联峰值抵消算法流程图

仿真结果如图6所示。

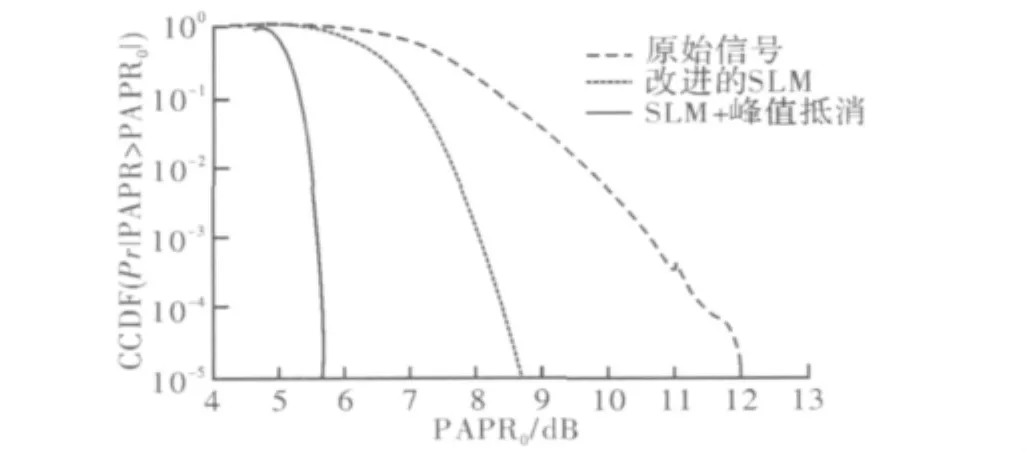
图6 SLM级联峰值抵消算法仿真图

由图6可知，基于m序列的SLM算法可以有效降低系统PAPR，且较传统SLM算法复杂度大为降低，PAPR改善约3.5 dB，当在改进的SLM算法之后增加抵消程度为3 dB的抵消信号后，PAPR将得到明显降低，PAPR值在5～6 dB之间，与改进的SLM算法比较，PAPR降低了约3 dB，由此可以看出，将降低SLM复杂度的改进算法与峰值抵消算法进行融合的改进SLM算法，可以更加有效地对抗系统的PAPR，并且不会产生较大的带外辐射。

图7 系统误码率性能

为研究在不同抵消程度下系统的误码率性能，图6比较了在AWGN信道中不同峰均比性能下系统的误码率(BER)性能。仿真结果表明，随着对系统的峰均功率比门限值的不断减小，系统的误码率有所增加，但相比没有经过SLM级联的限幅技术，误码率性能衰落很微小。

5 结束语

提出了一种基于SLM级联峰值抵消的PAPR抑制的改进算法，对系统PAPR性能有良好的改善。从仿真结果来看，基于m序列的SLM算法可以有效降低系统的PAPR，但所能达到的PAPR约为8 dB，当将其级联峰值抵消算法后，PAPR约降低了5.6 dB，且系统不产生带外辐射，但随着PAPR门限值的增加，系统的误码率性也降低，当抵消程度为3 dB时，与原始信号相比，误码率性能衰落很微小。因此，与传统SLM算法和峰值抵消技术相比，这种级联方式可以在较低误码率和带外辐射的基础上，明显改善PAPR的性能。

[1]HYUNG J K，SEONG C C，HYUN S，et al.Adaptive clipping technique for reducing PAPR on OFDM systems[C].VTC'2003-Fall，2003，3:1478-1481.

[2]GOLAYM J E.Complementary series[J].IRE Trans on Information Theory，1961，IT-7:82-87.

[3]BAUML R W，FISCHER R FH，HUBER J B.Reducing the peak-to-average power ratio of multi-carrier modulation by selected map-ping[J].Electronic Letters 24th，1996，32(22):2056-2057.

[4]MULLER S H，BAUML R W.OFDM with reduced peakto-average power ratio by multiple signal representation[J].In Annals of Telecommunications，1997，52(1-2):58-67

[5]汪裕民.OFDM关键技术与应用[M].北京:机械工业出版社出版社，2010.

[6]王文博，郑侃.宽带无线通信OFDM技术[M].北京:人民邮电出版社，2006.

[7]BREILINGM，MULLER-WEIFURTNER S H，HUBER J B.Distortion less reduction of peak power without explicit side information[C].Piscataway N J，USA:Conference Record/IEEE Global Telecommunications Conference v 3，2000:1494-1498.

[8]ZHOU Xuefu，JAMES C J.A new distribution bound and reduction scheme for OFDM PAPR[C].The Sth International Symposium on Wireless Personal Multimedia Communications，2002，l:158-I62

[9]尹长川，罗涛，乐光新.多载波宽带无线通信技术[M]北京:北京邮电大学出版社，2004.

[10]RUKHI N A，SOTO J，NECHVATAL J，et al.A statistical testsuite for random and pseudorandom number generators for cryptographic applications[EB/OL].(2003-09-12)[2010-09-12]http://csrc.nist.gov.

[11]FOSCHINI G J.Simplified processing for high spectral efficiency wireless communication employing mufti-element arrays[J].IEEE Journal on Selected Areas in Communications，1999(11):1841-1852.

[12]HIDEKI O，HIDEKI I.Performance analysis of deliberately clipped OFDM signals [J].IEEE Trans on Communications，2002，50(1):89-101.

[13]PANTA K R，ARMSTRONG J.Effects of clipping on the error performance of OFDM in frequency selective fading channels [J].IEEE Trans on Wireless Communication，2004，3(2):668-671.