洪水预报中的不确定性研究

2011-05-01 07:08英国布莱兹科瓦贝文

水利水电快报 2011年4期

[英国]S.布莱兹科瓦 K.贝文

李红梅译自荷刊《结构与基础结构工程》2009年第 8期

洪水预报中不确定性处理的方法在很大程度上取决于洪水的预报目的,例如,是用于实时预报还是用于洪水风险评估方面的模拟等。在实时预报中,主要目标是在利用事件中可以获得的任何数据,使得预见期精度最大化,并且预测变量的变化范围最小化。因此,这种方法应该是自适应的并且能充分利用同化数据。这种对于预报问题的自适应性意味着能用简单模型来代表系统,并且能超强适应不可避免的误差。如下文所述,可以用历史数据来建立这样的模型。

模型模拟的问题是各不相同的。在寻求最大的精确度和最小的预测不确定性的同时,对不同类型的应用都要求模型能以合适的方式代表水文过程,或者以合适的原因获得正确的水文预报值。这可能会带来一些问题。即使在流域研究中,也常会发生这样的情况:没有足够的信息来确定不明确的自然过程。实际上,获得流域出口的合理的流量模拟可以有很多不同的方式,研究人员把这种现象称为“殊途同归”现象 ,或称为 “模糊 ”、“非唯一 ”、“不可识别”的现象。研究人员用“殊途同归”这一术语暗示其不仅是在很多解决方法中择优,同时也表明所研究的问题具有普遍性。很多模型都可产生合理的结果,可以认为是有很多关于系统过程的假设在起作用,这些假设如果在有足够多的数据的情况下,有些可能得到验证,有些则被拒绝。

多种假设共同作用的方法是根据基于优化的模型率定所遇到的问题而采取的解决方式。这种解决方式当然很自然地将重点置于流域系统的模拟方面,尤其是模型显示出某些“最好”的统计特征,例如最小的误差变化等。然而,经验表明,好的模型可能会有很大的变幅,这取决于所使用数据的系列,而结果残差用常规的统计结构却难以表达。这并不奇怪,水文系统的自然过程模拟受制于每一个事件的输入,这就意味着有期望改变误差的分布。很显然,不合适的误差假设会导致不合适的结果。

如果有多种模型结构,不同的模型运行时的同一参数可能会有不同的值(或者是同一模型的不同方式运行时),这种情况还会更复杂。尺度问题也可能意味着合适的模型参数值可能会与实际测量值不同。而模型需要的有效参数值是由模型的结构决定的。

本文仅仅是研究洪水预报,重点是预报中的不确定性,提出了一种使用“殊途同归”的方法来解决问题及确定有效参数值。

1 洪水预报中的不确定性

在实时预报模型中,原则上是可以使用任何功能完备的降雨产流模型,概念性或者是基于物理的分布式模型。实时预报模型有很多种,但是基于数据的机理模型(DBM)却显示出有较大的优越性。这种模型主要是识别和评估能代表线性转换功能等动态行为的主导模型。非线性问题可以通过输入过滤功能来完成转换。假设在事件的过程中,知道关于降雨或者水位方面的信息,研究人员从处理不确定性出发,目标是预报误差变化范围的最小化。数据同化中一个重要的步骤是使用卡尔曼滤波方法(Kalman filter-based approach)更新预报值和评估预报中的不确定性因素。

基于数据的机理模型(DBM)能够用于产流和汇流的实时预报系统,基于数据的机理模型能和预报流量一样,准确地实时预报水位。这个模型有的是直接使用水位更新预报值,而不必用水位流量曲线将水位转为流量来更新预报值。通过避免水位流量关系曲线的非线性,该方法有望稳定预报变量的异方差,尤其是在发生漫岸流量的时候更是如此。

然而,仍然需要考虑一些非线性关系,例如降雨-水位预测和水位 -水位预测等。研究人员发现,存在于降雨 -水位或者降雨 -流量的非线性关系,能够用一个带有参数的指数关系来表达:

式中 uk代表过滤后的有效降雨;rk代表测量后的降雨;yk是水位或者是代表土壤湿度的流量;c是一个常数;γ是一个幂指数;k代表时间步长的序数。

对于流量或者水位与有效降雨之间的关系,可以采用线性转化函数来表达:

式中 a1…an和 b0…bm是系数;δ是一个时间推迟;k是时间步长的序数;ηk是噪声输入;uk是有效降雨。

经验表明,可以使用2个以上的系数灵活地确定降雨 -水位或者流量模型。这可以分解为一个快速响应和一个慢速响应来代表占主导的系统行为。使用卡尔曼滤波法进行数据处理是最简单的办法,可根据时间变增益来处理不断更新的预报值。其目的是在追求给定的预见期内预报方差的最小化。

2 模拟中的不确定性

洪水预报模拟在确定设计数据时,需要一定重现期的设计水文过程线,如预估一定重现期的洪水淹没范围,或者研究洪水产生机制等等。

通常,模拟方面的不确定性问题由两个部分组成,两个部分的不确定性都有多种来源。首先是预测在指定条件下的流量,尤其是不同重现期下的极端流量。其次是预测这些事件的影响,例如水库入流、洪泛区淹没面积、泥沙输移和财产损失等。这可能需要额外(不确定性)的模型模块。

在这两种情况下,预测的准确性将受制于模型输入的误差,某些系统特征的模型参数,模型率定所使用的数据,以及代表系统主导过程的模型结构自身的误差等。目前存在着很多结构复杂的流域径流产生模型,例如概念性模型(主要是基于很多水库概念的模型)和一些所谓的基于物理的模型(这些模型以一种分布式的微分方程表示)。将各个产流过程统合起来引入了越来越多的参数,以至于不能够很好地确定每个参数的意义,实测数据也没有足够的关于参数的信息用于模型率定。模型的参数由观测到的降雨径流数据率定得到,试图使用不经过参数率定的模型来进行降雨产流模拟肯定是不行的。

模型的校验一开始是由有经验的水文专家根据模型参数的物理意义手工完成,或者采用自动优化步骤完成。由于模拟过程的复杂性,模型的响应面也是复杂的,存在着很多局部最优值。研究人员花费了很多的努力,试图寻找有效的优化方法获得全局最优值。经验表明,相同模型的不同参数系列,或者是非模型的不同参数系列都能够得出同样的结果。模型的识别并非唯一,从这个角度来说,降雨径流模型和环境模型在数学上是不适宜的。因此,不可能将误差具体分解为多种误差源。

优化的参数设置对应于特定的模型输入系列。不同的误差可能会相互抵消,例如参数的误差可能会与某种输入误差相抵消。对于另外一套输入系列,研究者可能会得到另外一套最优化参数设置。解决这种问题的办法就是抛弃最优参数设置和最优模型的观念,并且对能产生合理结果的参数系列(有效参数系列)进行评估。计算的结果是可以从有效预测值的累积分布图上读出预测的包络线。

3 “殊途同归”理论和模型评估

“殊途同归”理论认为模型有很多合理的表达,并且不能轻易被拒绝,还要在预报不可确定性的评估中考虑。这就是研究人员使用的“通用不确定性评估”方法。

在“通用不确定性评估”方法中,参数系列是在物理成因的范围内随机设置,通常在参数设置前并没有关于参数值的信息,而是均匀取值。参数被用来实现不同的模型输出,然后再使用一定的标准进行检验,并且确定每个参数的权重。其中重要的一步是,如果参数不能得出令人可接受的模拟结果,则该参数需要被舍弃。“可能性”在这里比统计学上的“几率”范畴要广。确定“可能性”的措施包括观测流量和模拟流量之间的确定系数,这是一种基于观测数据和模型流量数据的频率曲线之间绝对误差之和,或者其他各种表达观测值与模拟值之间相似程度的模糊判别方法。在进行模拟以前,一些观测误差的范围如果能够确定,将会简化不确定性的分析过程。模型的模拟结果超出误差范围,都应被舍弃。

这种概念下的集合理论模型评估则十分简单,模型结果不在误差范围之内的都要被舍弃。这样可能有很多模型的模拟结果均在误差范围之内,并且会被接受。因此,任何这种类型的模型评估应当仔细考虑模型误差的不同来源,如前所述,这种误差评估在实际中是很困难的。模型误差的来源可以简化为输入误差、模型结构误差和实际测量误差。这些误差不能通过简单地比较观测值和预测值得到,在非线性模拟中,还没有通用的理论来指导分析不同来源的误差。大多数模拟者只是简单地认为这些误差数量相同,即使事实并非如此。因此,在评估模型的可接受程度的时候,有必要考虑确定合适水平的“有效观测误差”来考虑这些差别。这样定义以后,有效观测误差不必要有零均值或者是方差为常数,不必为高斯(Gaussian)分布,尤其是该种误差受着某种物理制约的时候。这样,任何有效模型都应该提供有效观测误差范围之内的模拟结果。

因此,对于一个有参数设置 Θ的模型,如果其所预测的变量 M(Θ,X,t)对于任何一个变量 Q(X,t)来说,满足:

则认为该模型是可以接受的。根据模型的可见性能,假设[Qmin(X,t),Qmax(X,t)]是观测值可能的范围,模型的“可能性”加权方式不一定非要使模型输出的结果在观测值Q(X,t)周围均匀对称,可能有其他多种分布形式。

这组简单的模糊隶属函数或者相对可能性方法适用于所有能提供预报的模型,其所提供的预报范围在可接受的范围之内。模型预报值与观测值很接近,赋予较高的权重;模型预报值超出观测误差范围则被赋予零权重。用这种方式对模型预报值进行限制,是基于如下隐含的假设,即模型预测中的误差与评估中的误差是相似的。

对于任何时刻的变量Q(X,t),如果预测值不在可接受的误差范围之内,则模型将被视为不可接受,并且要被舍弃。这与传统的统计模型不同,在那里一个错误的模型受制于模型结构,有时可能会被误认为是正确的,且在结构中补偿模型模拟的不足。如果没有一个模型被证明是理想的,那么表明,模型可能存在着概念上、结构上和数据方面的错误(尽管哪个原因是最为主要的仍然很难确定)。

所有模型的被拒绝或者被舍弃不能认为模型是失败,只是表明研究者需要了解更多的关于模型的系统结构、输入数据或者边界条件方面的信息。输入数据和边界条件是一个重要的考虑因素,因为即使一个“完善”的模型在输入数据有较大误差的情况下,也不能得到具有较高精确度的预测。所以需要将输入数据和边界数据的实际情况和模型参数共同进行评估,以确保模型误差是在观测误差的范围。最终结果是希望得到一些可接受的模型,每个模型赋有一定的可能性权重。

这种方法提供了一种比较好的模型检验和评估方式,通过假定有效的观测误差来避免对模拟误差进行假设。重点放在模型可预测变量和实际所观测变量在评价合理观测误差上的差异。

用散点图(将可能性空间的点投射到以单个参数为坐标轴的图上)可以说明模型的“殊途同归”理论和估计有效参数的可能范围。在大多数模型的应用中,只有1～2个参数是具有敏感性的,那些不敏感的参数在整个范围的模拟过程中能反应出模型是否可接受(图1)。图1为可能性散点,即确定性(图中的横轴为参数范围;纵轴为可能性检测;每个点为一次模拟)。

有时,模型需要考虑多个变量,例如在评估水力学模型的时候,出口的水文过程线和洪水淹没范围都可用作确定可能性。在评估洪泛区淹没范围的过程中,研究人员使用了一个淹没插值与观测值之间差异的方法,其方程式为:

还有研究者在评估洪水淹没范围的模型时是采用模糊方法,其结果是显示了一个给定流量下淹没范围的概率分布,提供一个未来事件淹没风险的简单评估办法。

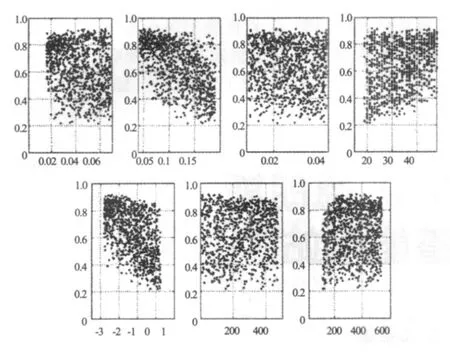
图1 可能性散点示意

在提供土壤含水量空间分布水文模型中,可能性评估方法是两个标准的组合,即流域出口流量模拟符合程度,以及土壤饱和模拟与实测区域的对比。

4 实例研究

下面用一个实例来讲述“通用不确定性评估”方法在热利夫卡(Zelivka)河流域洪水频率研究方面的应用。

研究流域面积为1186 km2,被分为7个子流域,其中 4个流域的流量信息是可以获得的。计算过程详见图2和图 3。模拟是使用的顶级模型(TOPMODEL)的频率模块进行的,该模型适用于在雨雪累积和融化的大型流域。

对于每个有观测数据的流域,设置一个模糊模型,同时结合以下 3个标准:即洪水频率曲线的拟合、洪水历时曲线和年最大水(雪)深(见图2)。

图2 短历时(100a)模拟可能性计算

在此基础上,对区域子流域模拟的可能性进行了研究。3个子流域的可能性评估,以及有长历时的观测数据的下克拉洛维采(Dolni Kralovice)站的流量频率可能性评估,坝址处洪水历时可能性评估,再加之跨流域融雪水当量评估,这些都是第2个模糊系统的输入。基于此,对以小时为单位的100a的短历时模拟进行了评估,然后用其参数进行了10000a的长系列模拟,以获得较长历时频率统计的较好评估。最后的评估也是以一种模糊的方式进行的,并使用了模拟降雨和最大可能降雨(PMP)的关系。预测的百分位通过从所有有效模型及相关的最终模糊可能性估计得到的预测值取权重来确定。图 3显示的是下克拉洛维采站的洪水频率曲线的包络线及观测数据。

图3 长历时(10000a)模拟可能性计算

5 结论

“通用不确定性评估”方法要求有很多主观因素,例如决定模型的参数,哪些是固定的,哪些是要变化的,以及参数范围、有效观测误差的合理范围、可能性的标准、输入数据和边界条件误差的处理等。然而,为便于分析和改变所有这些参数,都要精心考虑确定。例如对于洪水频率的评估问题,与终端用户讨论设计频率曲线的预测百分位是有必要的:他们是否会认为 95%的预测边界太高了?

最近几年,“通用不确定性评估”方法已经扩展为更加依赖与观测值有关的模型合理性的预估。这将会使人们的注意力集中到不可比较的误差(由于尺度或者不均匀性导致的预测值和观测值之间的差异),以及输入误差的影响方面,这两方面往往会被忽略。模拟只考虑预测值在有效观测误差范围之内的模型行为评估。