瑞士扩建格洛里特斯坝提高泄洪能力

[瑞士]M.比尔里 M.费德施皮尔 J.L.博伊拉特[法国 ]B.乌当 F.德洛米

胡卫东 译自英刊《水电与大坝》2010年第5期

对于格洛里特斯(Gloriettes)坝的扩建方案,考虑到几何与水力边界条件,除了尾水渠之外,两种不同形状的钢琴键型堰在瑞士的 EPFL水利建设实验室(LCH)通过物理模拟(比例尺1∶30)进行了试验与优化。

由于实测的水文数据增加并且研究开发了一些新方法用于洪水流量估算,社会上就有关安全方面的问题也提出了更高的要求,因此现有的许多大坝都需要对溢洪道进行改建,以提高它们的泄洪能力。正如其他许多国家的情况一样,就修改的设计洪水流量而言,已发现法国电力公司的数座大坝的泄洪能力不足。因而,提高溢洪道的泄洪能力,已成为水电工程管理者所面临的一个重要问题。

1 格洛里特斯坝

由法国电力公司(EDF)负责管理的奥德埃斯陶伯(Gave d'Estaubé)河上的格洛里特斯混凝土拱坝位于比利牛斯(Pyrenees)山山区,建于1949年至1951年间。最初的泄洪系统包括有坝顶高程1667 m处的 4孔自由溢流闸,在最高运行水位为1667.8m时,其泄流量约为70m3/s。对于重现期为1000a一遇的新设计洪水流量,洪峰流量定为150m3/s。为了弥补80m3/s的不足泄流能力,需要在右岸增修一座溢洪道,选用被称之为钢琴键型堰(PKW)的迷宫式溢洪道设计方案。设计了两种不同的堰顶形状,其堰顶高程与原有溢洪道的堰顶高程相同,并已通过了物理模型试验且进行了评估。

新 PKW坝址的下游属于岩土不稳定带,除了环境整体化的要求之外,不允许在尾水渠进行简单与直接的射流,但可用水流方向突变的方式替代。主要设计目的是产生连续的、最大的消能,以避免水流泛滥。

尾水渠的最初设计包括通过夹角为120°的曲线来相互连接的两段斜坡渠底(平面上成)直线的渠段,初步评价是基于分析水位、流速与消能。应用柏努利方程计算陡坡上水流的能头,消能以经典的科尔布鲁克 -怀特法(Colebrook-White approach)为基础。原来的设计只允许低水平的消能,从而导致流速过高(约25m/s)。采用标准的空化公式对渠底的空化指数(σ)进行了计算,结果表明,有数个渠段超过了临界值,即 σ＜0.2(空化风险)。

另一方面,采用纳普(Knapp)经验公式进行了计算,结果表明,在小半径的渠道曲线处形成的内外水深高达 6 m,这是由于离心加速度和驻波所造成的结果,鉴于这种水力特性,作出了具有两个阶梯型渠段与一个中间的消力池的归河渠道的完全新型的设计,要求方向改变120°(图1)。

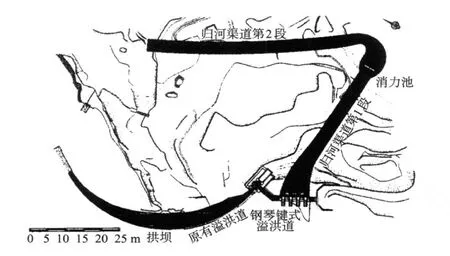
图1 归河渠道最终设计的平面布置

2 设计准则

2.1 边界条件

归河渠道的上游边界条件由 PKW确定。为了评估涉及到坝顶原有溢洪道的两种类型的 PKW的泄水能力,进行了数次试验。关于溢流堰系统的水力学问题,在雷特(Leite)等人(2009年)与比厄里(Bieri)等人(2009年)的著作中都进行了讨论。对于150m3/s的设计洪水流量,这些试验得出的归河渠道中最大泄流量为 80m3/s。采用一维数值模拟(HEC-RAS,version 3.1.3)对河道汇流处的水力学条件进行了计算,并对归河渠道的下游段以及奥德埃斯陶伯河天然河道的一部分进行了模拟,这段天然河段的泄流量为原溢洪道下泄的流量。简单的分析证明,渠道与河道的水流为亚临界流。河道的原有地形在渠道的倒数第2个阶梯上形成水跃,并且在汇流区还产生侧向溢流。

已经提出数次改进河道与渠道下游段形状的建议,包括局部加宽与疏浚,并在数值模型上进行了试验。但是,作为初步数值模拟结果,在物理模拟中未考虑汇流对归河渠道出流的局部会产生一定的影响。

2.2 阶梯渠道段

为了在两个渠道段上获得最大的消能效果,将阶梯沿渠道的纵剖面设置。初步设计是以最近研究的阶梯溢洪道工程为基础。低流量发生跌流水舌,大流量形成滑行水流情况。跌流消能是通过水流对阶梯的冲击进行的。因为阶梯间有截留的水体,滑行水流效率更低。当两种水流流态都部分存在时,这种流态称为渐变流。定义水流流态的公式(1)为渐变流;公式(2)为滑行流;公式(3)中 hc为临界水深;hs为阶梯高度;ls为阶梯长度;qw为单宽流量;g为重力加速度。

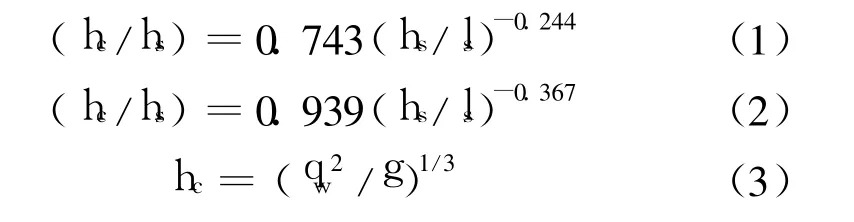
对于阶梯高度与长度的不同比值,消除的能量ΔH一般在有效水头 H0的 85%与 95%之间,水头损失 ΔH是根据实验建立的单宽流量和相对能量损失ΔH/H0两者间的关系进行估算的。这些结果是在试验水槽中按0.06 m阶梯高度取得的。对于1 m的阶梯,比例系数 λ为16.67,对于2m的阶梯,比例系数为33.33。相应的流量比例系数(λ5/2)分别为1.134与6.415。对于泄流量为 80m3/s,且渠道宽度为7.5m的条件,该情形为滑行水流,而且两个阶梯高度的消能率约为 90%。

对两个阶梯的高度(1 m与2m)和阶梯长度是可变的的情况进行了分析。在两种情况下,阶梯构造的主要设计标准则是避免溢流,并使开挖量最小,从而导致阶梯长度是变化的。已知两个渠道段的泄槽坡度θ,阶梯的法向高度 ks(公式4)和陡坡的佛汝德数 Fθ(公式5)是可确定的,并可导出混合均匀流的深度 Z90,u(公式 6)。这个水流深度相当于掺气浓度为 90%。

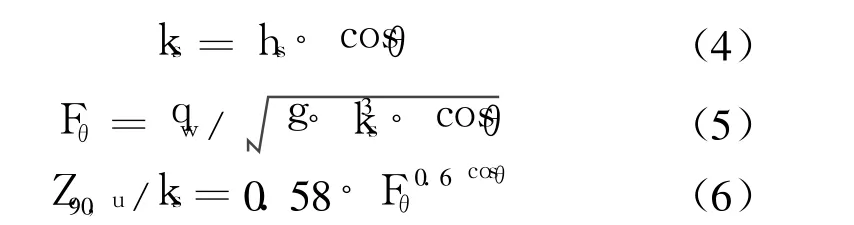
对于1 m和2 m高的阶梯,Z90,u大约分别为1.2m和1.3m。使用安全系数1.5,最大泄流量为80m3/s时,水深为2m。需要用这个深度来确定周边地形至渠底的高差Zs。它可以得出渠道底的下限线,渠道阶梯不应该超出这一下限线。由于阶梯很长,要求开挖的方量很大,而在经济上不可能接受2 m高的阶梯。

2.3 消力池

消力池必须能消除回水渠上段下游端处水流的剩余能量。消力池的布置与设计必须结合原有地形考虑,以便在第2段渠道的入口处得到临界水流条件,为了确保消力池突扩段具有令人满意的性能,已证实中央消力槛是有效的。消力槛的最优设计导致消力池内形成对称而且稳定的水跃,侧面漩涡对消能过程有明显作用的尾水流速分布近乎均匀。

对于给定的泄流量,入流深度 h1、水流速度 v1与第1段渠道出流处的佛汝德数 F1都能采用公式(6)进行计算。然后采用贝兰格尔(Bélanger)公式计算下游水流共轭水深 h2。对于 80m3/s的设计洪水流量,h1为1.1m;v1为9.7 m/s;Fr1为 3.0,结果h2为 4.1 m。

在麻城市石桥垸村，共同缔造活动实施了村庄环境提升、垃圾分类评比等工程，清理了杂乱的建筑，生活垃圾和污水收集处理更加规范，村里的水塘也通过专业的环保企业进行了治理，村庄环境得到明显改善。

按不莱梅(Bremen)法,消力池长度 xj用公式(7)确定。为了引导消力池曲线部分的水流流向出口,将 xj的计算值(约16 m)增加了5 m。

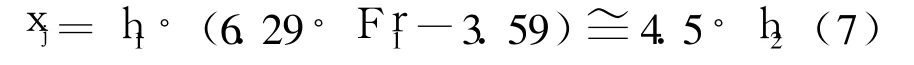
除了 h1和 b1之外,消力槛的最佳形状主要取决于 Fr1、消力池宽度 b2和渠道宽度 b1之间的扩展比。在目前情况下,b2(15 m)选定为 b1(7.5m)值的2倍。最佳水流条件通过高于0.8的无量纲的消力槛位置 Xp获得。考虑到入流部分逐渐扩大,Xp固定在1.75。相对于渠道出口的消力槛最优位置 xs可通过公式(8)确定,计算结果为6.5m:

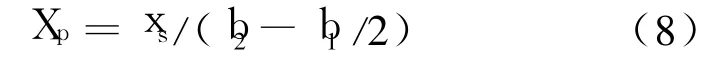
消力槛高度 s由公式(9)确定,等于1.6 m。

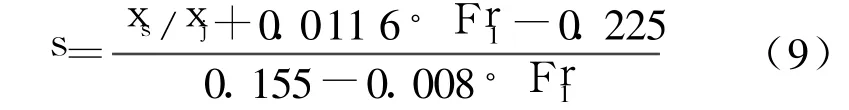
消力槛宽度 bs可用公式(10)计算,计算结果为9.4m。

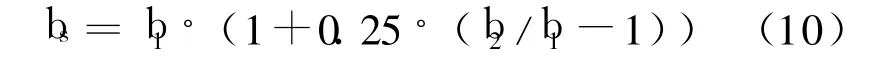
由于要求环境整体化,最初的模型构造和理论要求之间唯一的不同之处是消力池光滑而成圆形的边墙,因而水流流态十分相似。

3 物理模型试验

3.1 实验装置和测量设施

考虑到原有溢洪道格洛里特斯坝的新 PKW和归河渠道的水力学特性,认为采用1∶30的总几何比尺是恰当的,以避免缩尺效应。应用佛汝德相似性,这就意味着惯性力与重力之比保持不变。

模型包括两个相关联的部分。第一部分布置在正方形的钢板水池内,复制水库、拱坝和溢洪道。另一部分就是模拟归河渠道,在周边挡墙范围内对该渠道进行复制,允许在整个三维方向扩展。渠道段和消力池用 PVC制作。为了在回水渠道上开展试验,已将原有溢洪道关闭。这种措施可以对 PKW的下泄流量进行精确地控制,这一部分的流量由实验室的供水网络提供并用电磁流量计测量,钢板水池中的水位由两个超声波传感器控制,流速用精度为1 mm/s的微型螺旋桨测量,作用在消力池中消力槛上的静水与动水压力,由测压管和取样频率为100Hz的压力电阻效应传感器进行测量。

3.2 试验程序与优化过程

为了进行性能测试和优化,应用了一个迭代的系统程序。所有的试验最初都是按 80m3/s的设计洪水流量来完成的。优化后的结构体型则是用20m3/s、40m3/s和 60m3/s的较小流量进行验证。

第一步只是模拟、试验和改进归河渠道的第1段。为了检查水流的横向分布情况,测量了阶梯两边边界区的水位。紧靠 PKW下游的曲线部分的水流性状需要加以特别注意。已经制定了水流平衡与防止漫溢的两种综合措施,并进行了试验。一方面,通过降低转弯渠段内侧的高度和增加外侧高度,使阶梯成横向倾斜。另一方面,对阶梯的纵向体型也做了相应的修改。

此外,为了降低拱坝基础附近的漫流和冲蚀的风险,在外岸设置了一面导墙。不仅该结构的高度,而且其形状都是优化过程的组成部分。

第1段渠道下游的消力池的主要作用是允许方向在亚临界流条件下改变120°。简易而适宜的试验设施就可对消力池的几个单元进行优化。除了毗邻的天然地形之外,消力池的底部高程、周围的形状、入流和出流结构体型、消力槛的高度和形式都进行了系统的调整和定性的评估,而且对特大洪水情况下的消力槛上的静水和动水压力都进行了测量。为了从结构上确定有问题的频率,还进行了能谱密度分析。

为了模拟无覆盖开挖的岩石面的糙率,采用估计的原型不平整度为5～10cm,在渠道和消力池相对应的表面处增加了一层粗糙水泥浆。另外还在横向上敷设了一些约2 mm高和10mm宽的板条。原型上的实际糙率在理论上相当于斯特里克勒(Strickler)系数 35m1/3/s。

对于有无加糙层两种情况的最终外形,又测量了水位。对于两个渠道段末端处的出流流速,按规则网格采用微型螺旋桨进行了测量。亚临界水流的总体平均流速使得有可能估算其动能以及总水头,并最终估算对应的消能效率。

3.3 结 果

与上游部分有关的渠道第1段的优化,导致对横向倾斜的混凝土阶梯和边墙进行特殊的设计,以便避免漫溢。归河渠道的第2段平滑地弯曲,且其阶梯比第1段的阶梯长。在消力池的出口处,侧面导墙为获得适当的水流分布创造了条件。在第2段渠道的出口处,水流被安全地引导到朝向天然河道的轴线方向。

渠道两段出口处的平均流速使得计算消能效率、水头损失比与总水头之比成为可能。效率随流量增大而下降,这也是通过计算值预测的,计算值略低于实测值。对于低泄流量的水头损失进行了计算(对应跌流水舌情况),计算结果表明,其与实验结果非常相符。对于滑行水流情况,差别则是随泄流量增大而增大,不规则的阶梯布置以及渠道的曲率可能是导致这些差异的原因。对于粗糙层,在渠道出口处实测的流速较低,而结果是水头损失和消能效率较高。

消力池优化后的设计为方向上要求作120°变化创造了条件。它由一个开挖的圆池组成,并受到左岸和下游部分的侧墙的限制。为了在设计洪水条件下的消力池的水深稳定在 4m到5m之间,出口的宽度必须有6.2m宽,且必须由混凝土制作。最大水跃高度大约为 9m。消力槛位于距上段渠道出口5m处,最初确定的1.6m槛高是通过试验确认的。圆形消力池避免了侧面的回流区,但减小了过水断面。由于这个原因,槛宽缩短到7.5m,使其保持与渠宽一致。消力槛前部的实测压力约为5.3m水柱(见表1),且压力分布的左右点不对称,可以解释这是由于消力池的不对称形状引起的。1.3～1.9的标准偏差表明,变化很快的水流具有产生负压的风险。消力槛后部压力负荷约小50%。

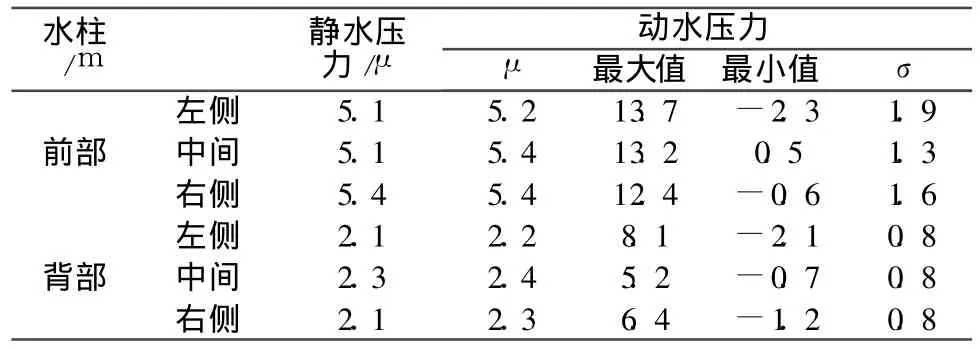
表1 设计洪水流量为 80m3/s时消力槛前部和后部实测的静水压力和动水压力

4 施工进度与费用

格洛里特斯坝位于法国高海拔的比利牛斯山脉的偏僻带。由于道路被雪覆盖且穿过几个雪崩区,在整个冬季期间不可能到坝址区。即使在夏季,从所有的公用设施到坝址都有很长一段路程。例如,驱车到最近的混凝土搅拌厂要1.5 h。

由于施工作业只能在夏季进行(从 6月开始到9月底),因此决定将工程分为2个阶段进行:

(1)第1阶段,在2009年夏季期间,主要工程包括第2段渠道、消力池及第1段渠道的下半部分岩石爆破与开挖,并修建消力池边墙和渠道段。

(2)第2阶段,在2010年夏季期间,主要工程包括第1段渠道上半部分岩石爆破和开挖、修建第1段渠道上半部分的边墙、锯混凝土墙和修建PKW。

由于拱坝布置在非常靠近开挖地区的位置,所以岩石爆破由位于大坝上和其基础周围的若干个加速计严格控制。2009年7月,对消力池与第2段渠道所在区进行爆破时,记录的最大速度为 4 mm/s,频率为 30Hz。

从地质学观点来看,新溢洪道和渠道段位于河流的右岸,此处由具有强烈的叶理构造方向垂直于河谷轴线的陡倾角片麻岩构成。岩石被先前的冰川割断和磨削,但岩质变化并不是非常严重。尤其是在消力池修建期间,遇到了一些地质难题,比如对粘土断层必须采用混凝土填充的乱堆来进行处理。

溢洪道扩建工程的总费用约120万欧元。主要费用与消能设施(渠道阶梯段和消力池)有关。

5 结 语

为了提高原有大坝的泄洪能力,采用了 PKW这种紧凑而适用的结构。这些结构向下游泄水往往需要采用原有的与创新性相结合的解决方法。格洛里特斯坝溢洪道扩建工程涉及到极其复杂的边界条件,包括120°的方向变化。有2个阶梯段与一个中间消力池的渠道结构布置方案,使得通过消能后引导水流到天然河道成为可能。通过理论方法预先设计几何特征,并通过物理模型试验进行优化,最终达到了以下目的:溢洪道中的水流为均匀流、消能效率大于 90%、开挖量最小,并满足与山区环境融于一体的要求。

所选择的方法涉及初步设计,是以最近研究的理论方法和简单的数值计算为基础的,随后在物理模型上进行系统试验。从技术与经济两个方面来说,这种方法是令人满意的。考虑到环境、结构和经济标准,迭代的试验程序加上适当的试验设备,使得解决复杂的工程问题成为可能。

目前该工程还在建设中。第1阶段的工程已于2009年10月完成,包括第1段渠道的下游部分、消力池与第2段渠道。PKW和第1段渠道的上部分工程目前正在继续施工中。