基于水动力学计算的气泡上升规律研究

缴 健 ，何生荣 ，李玉婷 ，罗玉峰

（1.河海大学 水利水电学院，江苏 南京 210098；2.水利部南京水利水文自动化研究所，江苏 南京 210012）

0 引言

河道流速是水文测验中的重要观测项目，目前一般采用流速仪法进行观测。该方法需要缆道或测船，费工费时且难以实现自动化和连续测流。为了解决上述问题，有学者提出使用河流流量测量的浮子式积深法，即利用浮子自河底上升至水面的冒出时间和随水流动的水平距离，计算得到河流垂线平均流速，进而达到流量测量的目的。可利用人工气泡发生装置从河底发生的气泡作为浮子。杨玉阁[1]根据实测资料拟合出气泡冒出时间和水深之间的关系曲线，论证了气泡作为浮子在小水深、低流速河流中测量流量的可行性。在气泡浮子法测流中，气泡冒出时间是影响测流精度的重要因素，因此其上升过程、速度等是需要重点关注的问题。

液体中气泡的上升运动规律问题，在化工、舰船等领域被广泛关注。Málaga 用积分法研究了稀释聚合物溶液中气泡形状[2]；Jiang 研究了假塑性流体中气泡群的混沌合并情况[3]；Basarová 研究了气泡与颗粒物体碰撞，得出理论模型，并对实际生产过程中气泡与大颗粒碰撞的轨迹误差进行了计算[4]。在气泡上升速度研究中，蒋炎坤根据试验数据拟给出了气泡加速阶段粗略的描述[5]。程文通过实验数据描绘了气泡终速度与气泡直径的关系曲线，并计算得到某一气泡直径上升终速度[6]60，但并未考虑加速段对上升速度的影响。刘胜通过公式推导给出不同流态下终速度与水深之间的关系曲线[7]，但未明确指出气泡直径对流态的影响。也有人关注到气泡在上升过程中由于压力变化所产生的形状变化问题，Amaya-Bower 利用格子波尔兹曼法对此进行了模拟[8]。徐炯试验结果表明，直径为 0.5～4.0 mm 的气泡，其上升高度与时间呈良好的线性关系[9]。程文通过试验观察，认为气泡直径在5.0 mm 以内可以认为是球形，5.0～8.0 mm 认为是椭球形[6]58。因此，为了排除气泡上升过程形状变化对上升时间的影响，用于浮子法测流的气泡直径不宜大于 5.0 mm。

采用气泡作为浮子进行流量测量目前尚处摸索阶段，首先需要研究静水中气泡沿垂线方向上升的运动规律，本文旨在针对直径为 0.5～4.0 mm 静水中的气泡上升规律进行研究，为采用气泡作为浮子进行流量测量奠定部分理论上的基础。

1 理论分析

气泡在上升过程中，受到浮力、重力及阻力的共同作用，气泡上升的动力学方程为[6]58

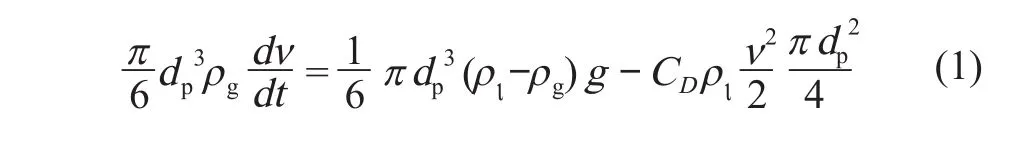
式中：ρι及ρg分别为液体及空气的密度；dp为气泡直径；g 为重力加速度，取 9.8 m/s2；v 为液体流动速度；CD称为阻力系数。

流体流动状态不同阻力系数 CD的计算公式也有差异，雷诺数可作为判别流体流动状态的准则，由流体力学颗粒雷诺数计算公式[10]可知，气泡雷诺数Re 计算公式为

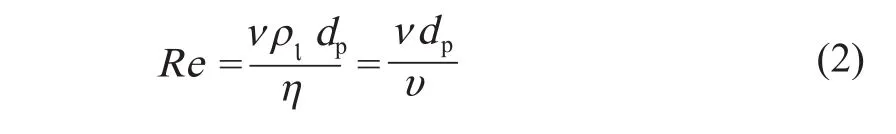
式中：η 为水的动力粘度：υ 为水的运动粘度。查液体粘度表可知，水在常温（20℃）下，η = 1.005×10-3Pa·s， υ = 1.007×10-6m2/s。

流态分别表述如下：

1）层流区（斯托克斯定律区，Re ≤2），CD可表示为

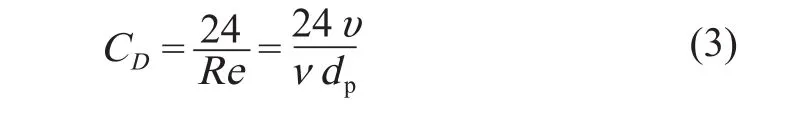
2）过渡区（阿仑定律区，2 ＜ Re ≤500），CD可表示为

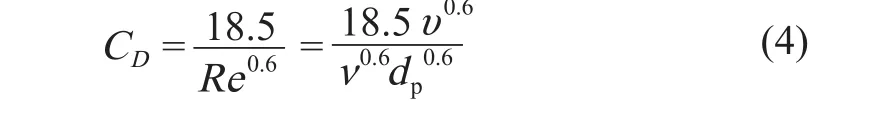
3）紊流区（牛顿定律区，500 ＜ Re ≤ 2×105），CD可表示为

4）紊流边界层区（Re ＞ 2×105），CD可表示为

根据气泡直径不变假设，气泡从发生到水面会经历先加速后匀速的上升过程。当加速度= 0 时，加速上升段结束，匀速上升段开始，对应的速度一般称为终速度。根据式 (1) 整理，可得最终速度的计算公式为

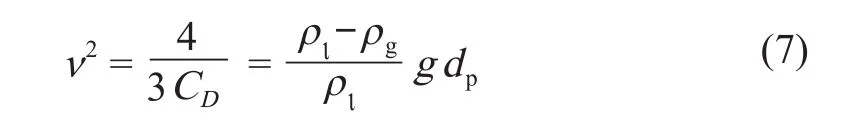
2 计算过程与结果

2.1 气泡上升最终速度

由于流态未知，故式 (7) 中 CD无法直接确定。在此采用试算的方法，即假定某直径气泡在最终速度时的流态，将式 (3)～(6) 代入式 (7)，约化后计算最终的速度，然后再根据式 (2) 计算雷诺数，检验假定的流态正确与否；若假定的流态不正确，则重新假定并计算验证，直至假定与验证相符为止。

经计算，直径为 0.5～2.0 mm 的气泡最终速度为0.0493～0.2404 m/s，颗粒雷诺数为 24.48～477.52，流态处于过渡区；直径为 2.0～4.0 mm 的气泡最终速度为 0.2405～0.3443 m/s，颗粒雷诺数为 520.31～1367.80，流态处于紊流区。因此，直径 0.5～4.0 mm的气泡匀速上升时雷诺数为 24.48～1367.80，流态在过渡区及紊流区，不存在层流区或紊流边界层区。计算结果如图 1 所示。

图1 气泡直径 dp 与上升速度 v 的关系曲线

图1 表明，直径为 0.5～4.0 mm 的气泡上升速度随直径增大而增大，以 2.0 mm 为拐点，在过渡区与紊流区最终速度与气泡均近似呈线性关系，且过渡区最终速度随气泡半径变化率较紊流区大。

2.2 气泡加速上升时间及高度

水中气泡上升存在先加速后匀速的过程，那么加速段所占的时间和上升高度如何，在整个上升计算过程中是否可以忽略？这是关系到能否进行简化计算的重要问题。

气泡从河底气泡发生装置冒出以后，初始速度为 0 m/s，随着上升高度的变化做变加速运动直至达到最终速度。根据式 (1) 可得加速度计算公式为

查密度表，取常温（20℃）下水的密度 ρι=998.20 kg/m3，空气的密度 ρg= 1.29 kg/m3。

由于雷诺数与气泡上升速度呈正比例关系，故若最终速度下的气泡处于过渡区，则其加速上升阶段的流态必经历层流区、过渡区；若最终速度下的气泡处于紊流区，则其加速上升阶段的流态必经历层流区、过渡区、紊流区。

当流态在层流区时，将式 (3) 代入式 (8) 得

当流态在过渡区时，将式 (4) 代入式 (8) 得

当流态在紊流区时，将式 (5) 代入式 (8) 得

由于阻力随速度的增大而增大，所以气泡在启动后至匀速上升之前，均作变加速运动。对式 (9)，(10)，(11) 进行一次积分可求得加速上升时间，二次积分可求得加速上升距离。针对直径分别为 0.5，1.0，1.5，2.0，2.5，3.0，3.5，4.0 mm 的气泡计算，并进行一、二次梯形积分，并以水深 0.1 m 为例计算气泡冒出时间。计算结果如表1 所示。

由表1 可知，若取水深为 0.1 m，气泡加速与冒出时间之比最大仅为 0.05710 %。如果水深增加，加速时间占冒出时间的比例会更小，因此可考虑将加速段速度按最终速度做近似处理，即气泡匀速上升。近似处理的误差分析结果如表2 所示。

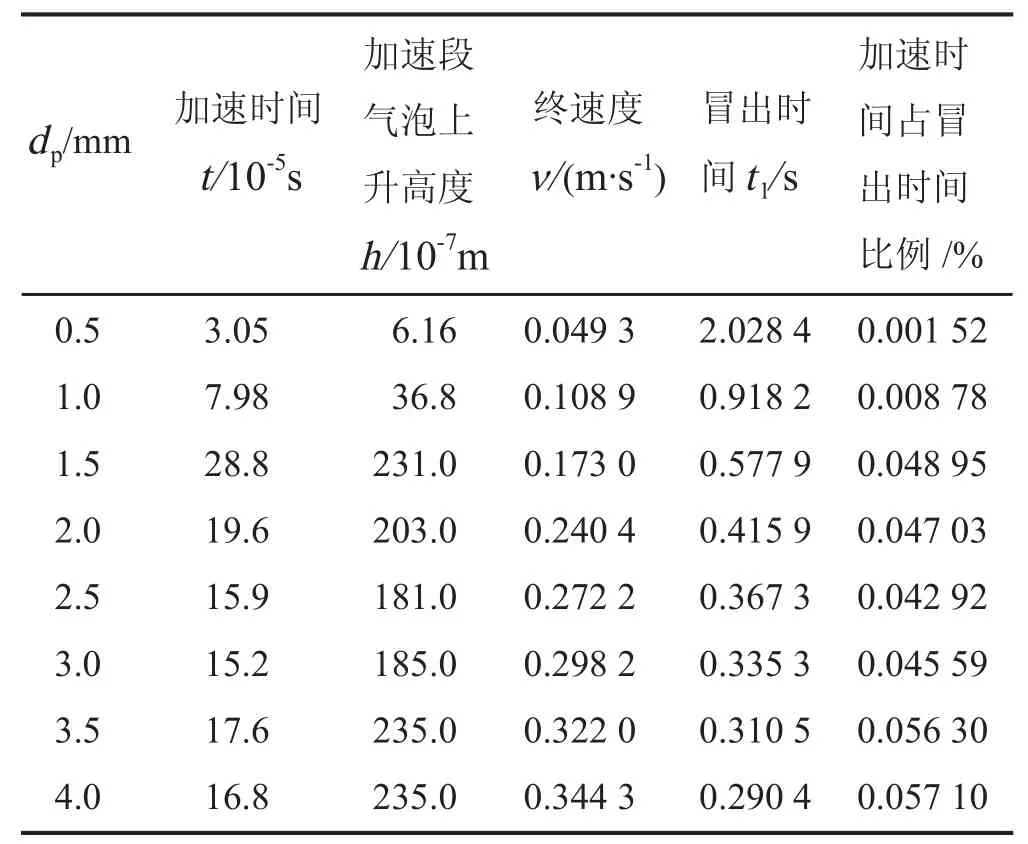
表1 水深为 0.1 m 时加速上升时间占冒出时间的比例

表2 冒出与近似冒出时间比较（水深为 0.1 m）

由表2 可知，当加速段速度近似取为最终速度，即认为气泡自河底发出至冒出做匀速运动时，冒出时间的最大误差仅为 0.023105 %，可忽略不计。由于水深越大加速段占总上升过程的比例越小，所以一般情况下可以将气泡整个上升过程视为匀速运动。

2.3 不同直径气泡冒出时间与水深之间的关系

根据以上结果，将气泡整个上升过程视为匀速运动，即可根据直径与速度关系求出气泡冒出时间与水深的关系。以 1.0，2.0，3.0，4.0 mm 直径气泡为例，计算结果如图 2 所示。

图2 表明，气泡冒出时间与水深呈线性关系，这是由于气泡上升过程按照匀速运动处理；相同水深下，气泡直径越大，冒出时间越短。

图2 不同直径气泡冒出时间与水深关系线

3 结语

气泡从河底发生装置发生至冒出过程中，先经历变加速过程，达到最终速度后作匀速上升运动。根据计算，得出以下结论：

（1）对于直径在 0.5～4.0 mm 的气泡，直径在[0.5，2.0]mm 区间时最终速度的流态处于过渡区，在 (2.0，4.0]mm 区间时最终速度的流态处于紊流区。

（2）气泡加速段经历不同流态，其时间与高度占总体比例极小，将加速段近似看作以最终速度作匀速运动对气泡冒出时间的计算结果影响甚微，所以可对气泡上升全过程近似做匀速处理。

（3）对于直径在 0.5～4.0 mm 的气泡，气泡直径越大，最终速度越大，在水深一定的情况冒出时间越短。

[1]杨玉阁，陈祖辉. 气泡上升规律的研究与应用[J]. 东北水利水电，2010 (10): 47-48.

[2]Málaga C, Rallison J M. A rising bubble in a polymer solution [J].Journal of Non-Newtonian Fluid Mechanics,2007,141 (1): 59-78.

[3]Jiang S, Ma Y, Fan W, et al. Chaotic Characteristics of Bubbles Rising with Coalescences in Pseudoplastic Fluid [J].Chinese Journal of Chemical Engineering,2010,18 (1):18-26.

[4]Basarová P, Machon V, Hubicka M, et al. Collision processes involving a single rising bubble and a larger stationary spherical particle [J].International Journal of Mineral Processing, 2010, 94 (1-2): 58-66.

[5]蒋炎坤. 水下排气气泡运动特性及其数值模拟研究 [J].华中科技大学学报（自然科学版）， 2004 (10): 49-50.

[6]程文，周孝德，郭瑾珑，等. 水中气泡上升速度的实验研究 [J]. 西安理工大学学报，2000 (1): 57-60.

[7]刘胜，杨成渝，王平义. 水中气泡运动规律的研究 [J]. 重庆交通学院学报，2007 (3): 136-139，152.

[8]Amaya-Bower L, Lee T. Single bubble rising dynamics for moderate Reynolds number using Lattice Boltzmann Method[J].Computers & Fluids, 2010, 39 (7): 1191-1207.

[9]徐炯，王彤，杨波，等. 静止水下气泡运动特性的测试与分析[J]. 水动力学研究与进展 A 辑，2008 (6): 709-714.

[10]谢振华. 工程流体力学[M]. 3 版. 北京：冶金工业出版社，2007:170-173.