箭载GPS实时定位滤波算法研究

赵树强,许爱华,苏 睿,王家松

(1.宇航动力学国家重点实验室,陕西西安710043;2.中国西安卫星测控中心,陕西西安710043)

0 引 言

目前,运载火箭GPS实时定位多采用运动学方法,利用最小二乘法解算火箭的弹道参数,该方法模型简单,无需了解动态接收机动力学模型,基本满足数据处理精度要求,但存在弹道参数随机差较大的缺陷。在箭载GPS动态定位中,动态接收机天线是一个遵循一定规律不断变化的动态系统。在不同时刻对该系统的状态进行观测,各观测量历元间存在一定的相互关系[1],而最小二乘难以充分利用历元间这些规律和相互关系进行数据处理。为消除高动态GPS定位数据中的随机误差,就必须应用最优估计方法将真实的状态从各种随机干扰中实时地估计出来。卡尔曼滤波是在线性无偏最小方差估计原理下,导出的一种递推滤波方法。它引入了状态空间的概念,借助系统的状态转移方程,根据前一时刻的状态估计和当前时刻的观测值,递推估计新的状态估值。因此,卡尔曼滤波更适合箭载GPS动态定位的数据处理。利用从GPS卫星信号获得的具有噪声误差的离散观测量序列,建立动态模型来描述箭载GPS接收机随运载火箭的运动状态,其中被估计信号是由白噪声激励引起的随机响应,激励源与响应之间的传递结构已知,量测量与被估计量之间的函数关系也已知。因此,在箭载GPS动态数据处理中可将卡尔曼滤波用于GPS数据的实时定位,能有效减小弹道参数的随机误差,提高定位精度。

1 箭载GPS动态滤波数学建模

箭载GPS实时定位一般都将GPS卫星轨道视为已知[1-5],利用观测值就可以直接求解运动载体的位置速度,而无需任何作用于目标上的作用力的信息。因此,运动载体的动态模型(状态方程),可以用动态位置、速度和加速度来表示。动态模型难以用精确的数学公式表示[3-4],在实际应用中,一般都是在保证一定精度前提下,采用简化的动态模型,常用的模型包括常速度、常加速度模型[1-2]。采用哪种模型,取决于运动载体的运动状态和采样率的高低。在高动态箭载GPS定位中,数据采样率一般都为0.1 s或更高。在此情况下,可采用常加速模型,且假定动态噪声为零均值高斯噪声。

1.1 系统模型的构建

动态方程为

式(1)中,Φk,k-1为非奇异状态一步转移矩阵;Wk-1为系统在tk-1时刻的状态噪声向量,为零均值的高斯白噪声随机序列,即

式中:Qk是系统的过程噪声向量序列Wk的方差矩阵,为对称非负定矩阵;δkj是 Kronecker-δ函数,其定义为

状态转移矩阵为

其中:

则系统噪声方差矩阵为

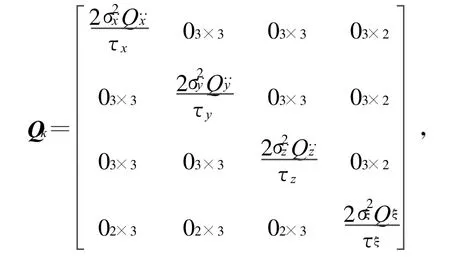
《杂文月刊》文摘版2018年10月下中姚正安老师写的《熟人生处》，读后收益很大。我把这篇文章让妻子和上大学女儿认真去阅读，让她们明白一个很浅显的道理，这就是家人之间也要“生处”，这样家才能真正变成温馨的港湾。

Q﹒ξ为观测历元间隔。

1.2 系统测量模型的建立

设箭载GPS接收机在k时刻同步观测到n颗GPS卫星的伪距和伪距率,则观测矩阵可表示为

线性化方程为

其中:

伪距ρik的非线性公式为

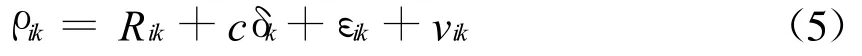
对于多普勒频移可表示为

2 箭载GPS动态滤波定位计算分析

利用箭载GPS数据进行处理,该数据格式为专用格式,采样间隔为每秒10点。系统加速度噪声给定(10-5)2,伪距测量噪声为22,伪距率测量噪声为0.12,协方差矩阵的初值给定为

首先对箭载GPS观测数据进行预处理,然后进行最小二乘(LS)计算和卡尔曼动态滤波,处理流程见图1所示。

图1 箭载GPS实时定位滤波流程图

图2给出卡尔曼滤波和最小二乘(LS)定位结果位置分量和速度分量的互差曲线。从图中可以看出,卡尔曼滤波结果与LS定位结果在X、Y、Z方向位置差都在±10 m范围内波动,X、Z方向速度差在±0.5 m/s范围内,Y方向速度差在±1.0 m/秒范围内。由此可见,卡尔曼滤波结果与LS定位结果吻合度很好。

表1为LS和卡尔曼滤波定位结果位置分量和速度分量随机误差的统计表。图3为LS和卡尔曼滤波位置分量和速度分量随机误差比对曲线。

从表1中可以看出,LS方法得出的GPS定位结果在X、Y、Z三个方向上的随机差在1～2 m,而卡尔曼滤波方法能使三个方向的随机差都大大下降,达到1 cm左右。对于速度分量,卡尔曼滤波方法也能使三个方向上的随机差减小一个量级。

表1 LS和kalman滤波位置和速度分量随机误差的统计表

从图3中可以明显看出,卡尔曼滤波方法的随机差都明显小于LS方法,而且随机差分布的更加均匀,这说明运载火箭的GPS接收机在高动态、高采样率情况下能较好地匹配均加速模型,适合卡尔曼滤波的解算方法。需要说明的是,统计的随机误差较大的地方是弹道特征点附近,接收机在特征点前后测量数据有个别失锁现象,但其统计结果也优于LS方法。

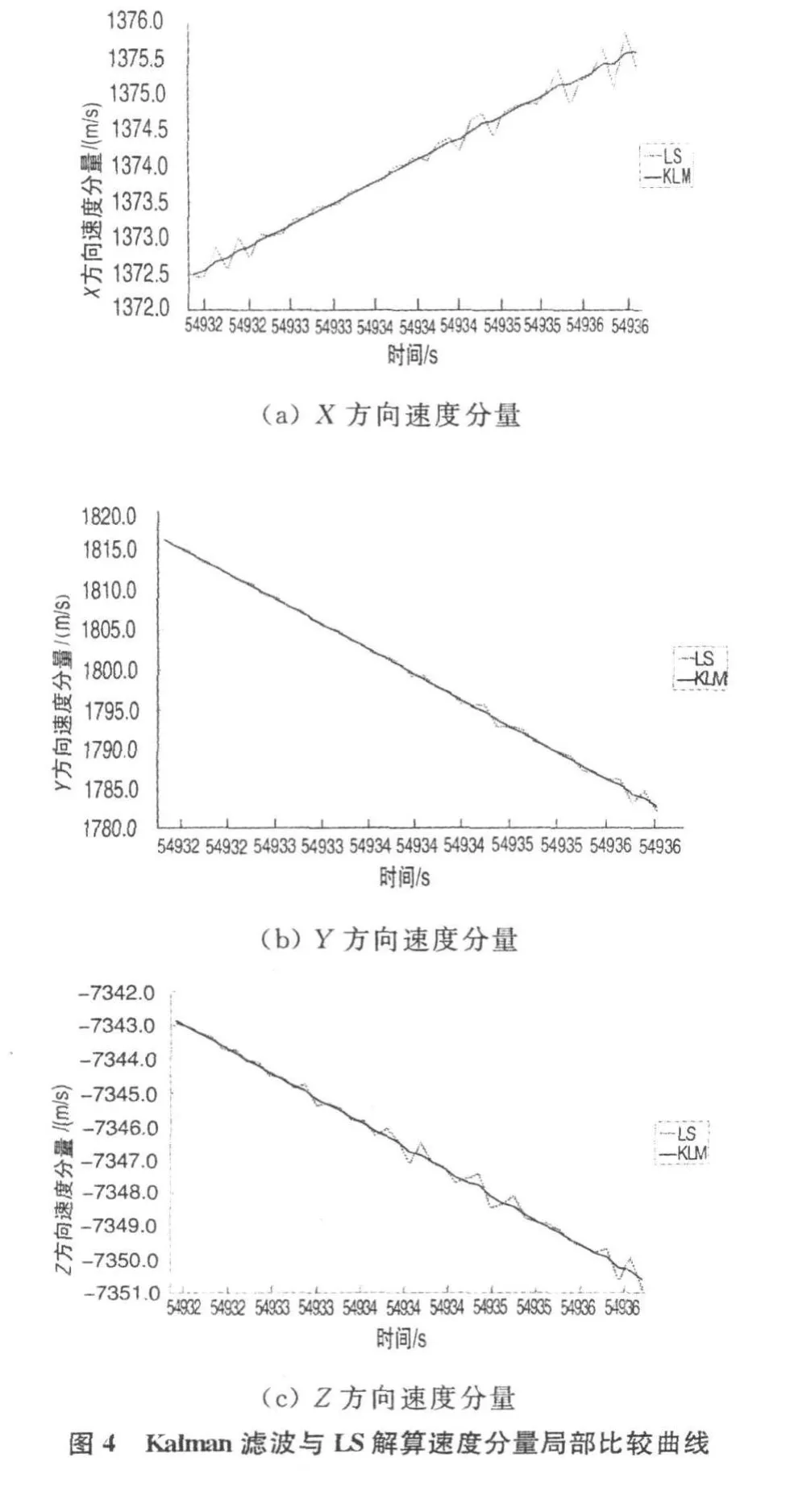
图4为速度分量局部曲线,从图中可以看出,卡尔曼滤波解算出的火箭弹道在 X、Y、Z三个方向的速度分量都比LS的结果更加光滑,更符合火箭弹道的实际飞行情况。

3 结 论

针对最小二乘在箭载GPS实时定位中的缺陷,研究了箭载GPS动态定位实时算法,给出了滤波的动态定位模型,并利用实测数据进行了分析计算,从以上结果分析可以看出,箭载GPS动态滤波计算的弹道参数随机误差在位置分量减小一个数量级,速度分量的随机误差比最小二乘方法减小至少50%,有效地提高了火箭GPS弹道参数的精度。同时,与最小二乘相比,动态滤波不进行迭代运算,矩阵的运算量相对较少。经统计验证,每个历元的弹道参数解算都能在10 ms以内完成,远小于10 Hz的采样间隔时间,能很好满足实时定位的要求。

本算法能有效抑制高动态情况下的随机误差,具有高精度、低复杂度等特点,可进一步推广应用于导弹、航天器或飞机试飞等高动态GPS实时定位中。

[1] 万德钧,房建成,王 庆.GPS动态滤波的理论方法及其应用[M].南京:江苏科学技术出版社,2000.

[2] 张守信等.GPS技术与应用[M].北京:国防工业出版社,2004年.

[3] 付梦印,邓志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003年.

[4] 杨元喜,张双成,高为广.GPS导航解算中几种非线性Kalman滤波的理论分析与比较[J].测绘工程,2005,14(3):4-7.

[5] 文援兰.卫星导航系统分析与仿真技术[M].北京:中国宇航出版社,2009年.