航空推进系统性能寻优控制的系统模型
尹大伟,樊照远,廖 瑛
(1.国防科学技术大学航天与材料工程学院,长沙 410073;2.海军驻沈阳地区发动机专业军事代表室,沈阳 110043)
1 引言
随着数字式电子控制器和软件技术的发展,现代控制理论开始应用于航空发动机控制领域。20世纪80年代末,美国NASA开始航空推进系统性能寻优控制(PSC)研究,并将其在配装F-15战斗机的F100系列发动机上在亚声速和超声速飞行条件下成功地完成几种模式的飞行试验[1,2]。大量的仿真计算和飞行试验表明,性能寻优控制技术的应用,使发动机的推力增大、耗油率降低和涡轮进口温度降低,极大挖掘发动机潜能[3]。
性能寻优控制是基于模型的连续寻优控制,因此各个步骤所采用的模型是其关键技术之一[4]。
对于航空推进系统性能寻优控制技术,国内外进行了大量研究[5~7],根据模型不同,主要采用2种技术方案:(1)通过求解发动机部件性能参数退化量修正基准模型[8];(2)是通过求解可测参数偏离量修正基准模型[9,10]。本文主要采用第1种方案进行系统模型分析。
2 性能寻优控制模型选择
PSC是基于模型的控制,通常要求模型准确和计算实时性,即要保证计算速度。但是,精确的模型往往很复杂,无法满足实时计算的要求。对于航空发动机部件级非线性模型,复杂气动热力计算和多维隐式非线性方程组求解在现有运算能力的机载控制计算机上很难实现实时。性能寻优控制为保证实时计算,各部分模型都简化处理,主要途径是给定参考工作条件,在一系列选定的基准工作点,对非线性模型线性化得到简化的分段线性化模型,通过相似变换可获得全包线内分段线性化模型。所建简化线性模型虽然能够满足快速计算的要求,但是显然无法满足高精度要求,因此,采取对简化模型进行修正的策略,以同时满足计算精度和速度的要求,这是性能寻优控制中解决模型精度与计算速度矛盾的基本原理[3]。
根据PSC原理,认为参数的基准模型计算值与测量值不一致是由部件性能退化引起的,由部件性能参数退化量(EDP)来修正基准模型,以达到相关参数计算值与测量值一致。因此,需要建立相应的模型,采用适当的算法求解部件性能退化参数退化量。该模型仍需满足实时计算的要求。根据前面模型精度与计算速度分析,建立估计所用的分段线性化模型,选择线性估计算法Kalman滤波器估计EDP。最终的性能优化算法在实际工程实现时,也是采用线性最优化的方法优化修正后的线性化推进系统模型,以保证计算速度。因此,性能寻优控制的系统组成、各部分模型以及算法选择的基本原则是保证实时计算和通过修正计算提高模型的精度。这种在线的模型实时修正即为相关研究文献中所描述的机载自适应模型[11]。
3 性能寻优控制模型描述
根据推进系统性能寻优控制的基本原理,性能寻优过程主要包括参数估计、模型修正和性能寻优。其主要模型包括2类:(1)是用于采用Kalman滤波器求解发动机性能退化参数的估计模型;(2)是推进系统稳态模型,是进气道、发动机和喷管的综合模型。这2类模型都是在选定的稳态基准点处的线性化模型,模型系数矩阵存储于控制计算机中,当前工作模型根据飞行参数进行选择。如前所述,由于是在线性能寻优,对寻优计算速度要求很高,为保证计算的快速性,需要采用的模型尽可能简单,因此,各环节采用的模型都是简化模型。系统模型的总体结构如图1所示(只考虑单独的推进系统性能优化,未考虑飞行/推进综合优化)。
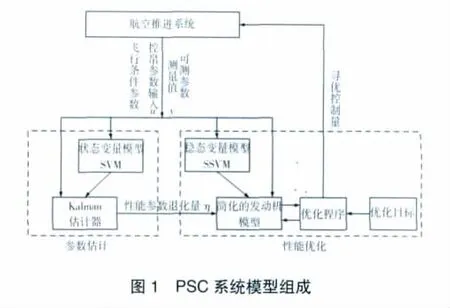
3.1 估计模型
估计模型是Kalman滤波算法估计性能参数退化量所用的模型,通常称为状态变量模型(SVM)。SVM是在参考飞行条件下,根据发动机非线性模型,在选定的基准点处进行线性化而获得的分段线性化模型。对不同选定的基准点模型系数矩阵,进行离线计算,存储在机载计算机中,模型覆盖标准发动机工作范围。估计模型还包括所用的基准点值表。
状态变量模型描述为
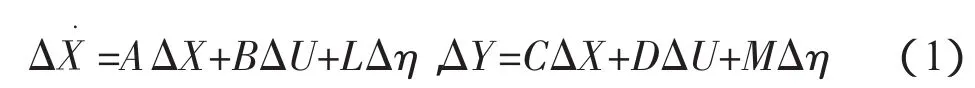
式中:ΔX=X-Xb,ΔY=Y-Yb,ΔU=U-Ub,分别为相对于基准点的状态增量、可测输出增量和控制输入增量;Δη为待估计的性能参数退化量。
具体应用时只需根据不同型号发动机选择相应的状态变量(高、低压转子转速)、可测参数(如低压涡轮进口总温、加力燃烧室进口总压等)和控制输入参数(如供油量、喷管喉部面积等),通过相似变换获得全飞行包线模型。为了估计性能参数退化量,将Δη作为扩展状态变量,则SVM记为
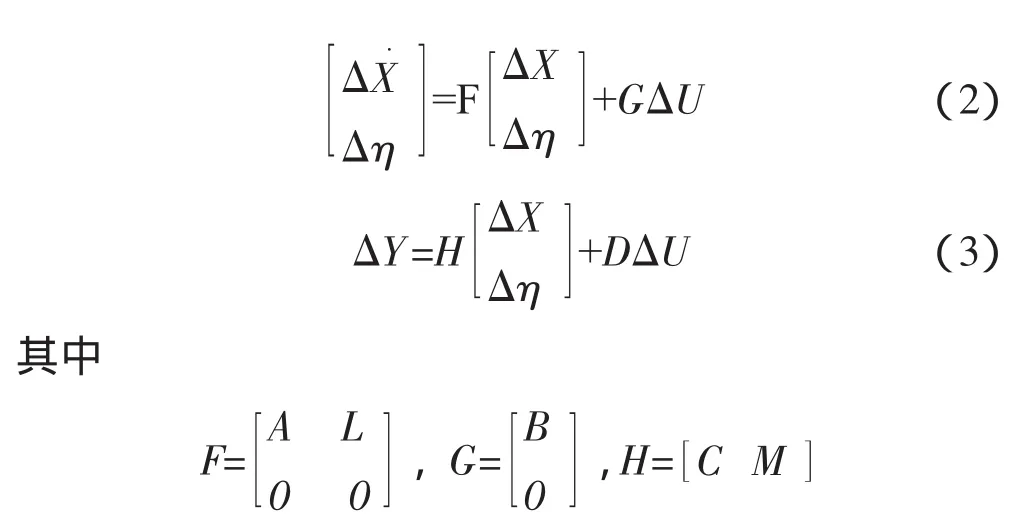
根据系统状态模型和测量参数值,采用Kalman滤波算法可估计出各计算基准点的部件性能退化量Δη。根据Kalman滤波稳定的条件,要保证估计结果收敛,需要保证系统能观测的要求,对于上述模型,系统能观测的必要条件是可测参数个数不少于待估计的性能参数个数,即 dim(Y)≥dim(Δη)。
算法实现时,根据选定的查表用测量参数值,通过查表选择当前的模型系数矩阵和当前的计算基准点。以F100发动机性能寻优的实现为例,参考飞行条件:飞行马赫数为0.9,飞行高度为9144 m,选择的49个基点覆盖了发动机推力调整范围,通过燃烧室出口总压Pt4值确定当前工作模型(最初的Pt4不是可测参数,由发动机进口总压Pt2和可测的燃烧室静压PB计算得到,后来Pt4改为可测参数,范围是16.17~182.80 g/mm2),为避免模型的频繁切换,选择与当前Pt4最接近的对应矩阵组,即SVM[11]。估计模型结构如图2所示。

3.2 性能优化模型
性能寻优控制最终采用优化算法优化发动机性能参数,为保证计算速度仍采用简化模型。简化的推进系统稳态模型(CPSM)包括2个子模型:简化的进气道模型(CIM)和简化的发动机模型(CEM)。进气道模型包括亚声速CIM和超声速CIM。本文主要分析简化的发动机模型。
简化的发动机模型是由非线性的气动热力模型分段线性化的稳态公式,称为稳态变量模型(SSVM)。稳态变量模型根据基本模型和前1步辨识出来的性能参数进行模型修正。
加入性能参数修正的SSVM表达式
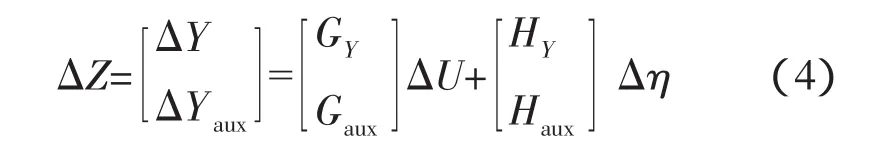
式中:下标aux为需要计算的不可测参数;ΔY、Yaux分别为可测输出和不可测输出参数的增量;ΔZ统一代表工作过程输出参数增量。
式(4)中代表不同工作状态的模型矩阵同样基于选定的基准点分段线性化离线计算得到的,并根据基准点列表存储,通过插值来确定当前的模型矩阵。以F100发动机PSC为例,当前模型矩阵是根据燃烧室出口总压Pt4和加力燃烧室进口总压Pt6插值获得[11](Pt6为可测参数)。
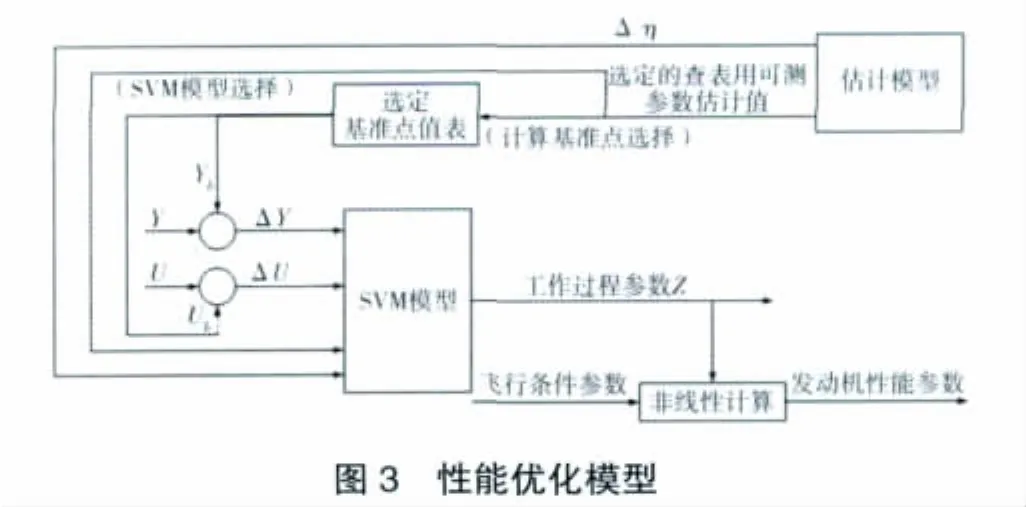
根据所建立的SSVM计算得到工作过程参数,由该参数通过非线性计算可求得推力、耗油率、喘振裕度等发动机性能参数,加上发动机稳定安全工作约束,如高压涡轮进口温度、压气机喘振裕度等限制,选择优化算法对选定的性能参数进行优化计算,可得到优化后的控制参数。根据NASA对PSC前期的研究,基于简化线性模型的性能寻优,采用线性规划算法作为优化算法,保证计算速度。性能优化模型结构如图3所示。
4 结束语
根据航空推进系统性能寻优控制的基本过程和原理分析了相关系统模型。描述了PSC中状态变量模型(SVM)和稳态变量模型(SSVM)及实际应用时模型选择的方法。随着计算机技术的发展,运算速度将不断加快,可能采用非线性参数辨识和非线性优化算法,直接使用航空发动机非线性气动热力模型完成计算,可进一步提高模型的精度。因此,非线性性能寻优控制技术也是目前和今后该领域的重点研究方向之一[5,10,12]。
[1]Golyard G, Orme J. Subsonic Flight Test Evaluation of a Performance Seeking Control Algorithm on an F- 15 Airplane[R].AIAA- 92- 3743.
[2]Orme J S, Conners T R. Supersonic Flight Test Results of a Performance Seeking Control Algorithm on a NASA- 15 Spacecraft[R]. AIAA- 94- 3210.
[3]Gilyard G B, Orme J S. Performance- seeking Control - program Overviewand Future Directions[R]. AIAA- 93- 3765.
[4]袁春飞,姚华,杨刚.航空发动机机载实时自适应模型研究[J].航空学报,2006,27(4):561-564.
[5]吴丹.航空推进系统非线性性能寻优控制研究[D].西安:西北工业大学,2004.
[6]欧阳舟.航空发动机部件性能跟踪滤波器研究[D].西安:西北工业大学,2004.
[7]朱之丽,王晓波.高推重比涡扇发动机性能寻优分析研究[J].航空动力学报,1999(3):260-264
[8]Luppold R H, Gallops GW, Kerr L J, et al. Estimating In- Flight Engine Performance Variations Using Kalman Filter Concepts [R]. AIAA- 89- 2584.
[9]Alag G, Gilyard G. A Proposed Kalman Filter Algorithm for Estimation of Unmeasured Output Variables for an F100 Turbfan Engine[R]. AIAA- 90- 1920.
[10]袁鸯.发动机自适应建模与神经网络控制[D].南京:南京航空航天大学,2005.
[11]Maine T, Gilyard G, Lambert H. A Preliminary Evaluation of an F100 Engine Parameter Estimation Process Using Flight Data [R]. AIAA- 90- 1921.
[12]王芳.航空发动机性能寻优控制研究[D].西安:西北工业大学,2005.

