涡轮盘低循环疲劳可靠性设计方法

高 阳,杨昌军,白广忱,林 垲

（1.中航工业贵州航空发动机研究所，贵阳 550081；2.北京航空航天大学能源与动力工程学院，北京 100191）

1 引言

随着现代航空发动机对结构可靠性要求的提高，发动机典型结构可靠性设计分析方法已经成为高推重比发动机研制的关键技术。作为发动机关键部件，涡轮盘在高温、高转速下工作，其低循环疲劳寿命受到结构几何尺寸、温度、转速和材料性能等众多随机因素的影响。近年来，国内涡轮盘疲劳寿命可靠性研究主要集中在寿命概率模型[1～4]和可靠性分析方法[5～7]研究。在涡轮盘结构低循环疲劳可靠性设计分析中往往只考虑材料循环应变-寿命曲线分散性的影响，而忽略材料循环应力－应变曲线分散性的影响。大量疲劳试验证明，循环应力－应变曲线同样存在较大分散性，导致在同样载荷条件下结构的应变响应呈现随机性，进而影响结构低循环疲劳寿命的概率评估。

本文基于现有疲劳试验数据，建立了涡轮盘材料GH4133合金的循环应力－应变概率模型，提出涡轮盘低循环疲劳可靠性设计方法。

2 循环应力－应变概率模型

弹塑性材料的循环应力－应变曲线可以表示为

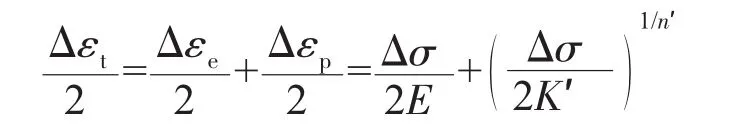
对弹性应变分量和塑性应变分量分别取对数得到

因此，对应弹、塑性应变分量的随机线性方程可以表示为

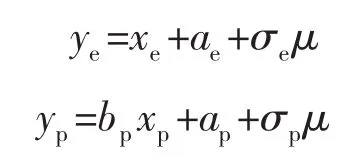
式中：μ为标准正态随机变量，则一定温度下材料循环应力-应变概率模型可以表示为[8]

根据文献[9]中GH4133合金在250、400和500℃下的疲劳试验数据，计算得到250℃下循环应力-应变概率模型

400℃下循环应力-应变概率模型

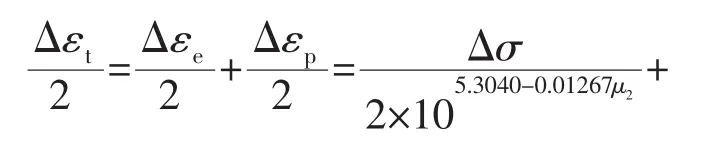
500℃下循环应力-应变概率模型

式中：μ1、μ2、μ3均为标准正态随机变量，分别描述了250、400和500℃下GH4133合金循环应力-应变曲线的分散性。

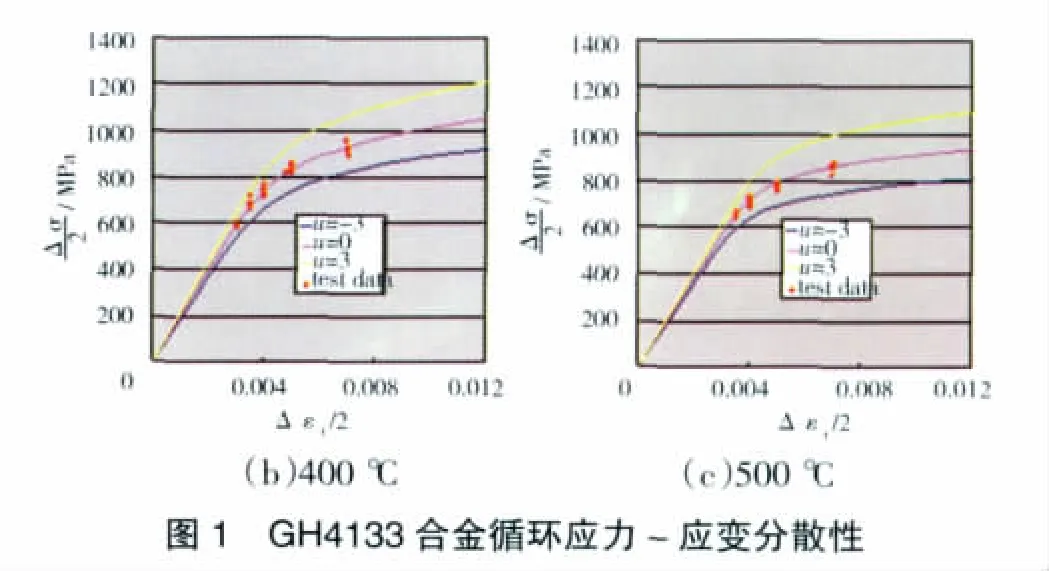
在涡轮盘结构概率分析中，如果将表示不同温度下循环应力 -应变曲线分散性的 μ1、μ2、μ3作为相互独立的随机变量，则可能会出现在相同应力水平的高温条件下，其应变值反而小于低温条件下的应变值的情况，很明显与实际情况不符。另外，由于疲劳破坏试验不可能得出同一试件在不同温度下的循环应力- 应变响应，因此也难以获得变量 μ1、μ2、μ3之间的相关性。为此，假设同一试样在任意温度下测定的循环应力-应变曲线所对应的概率百分位是定值，即假设μ1=μ2=μ3。则在涡轮盘结构概率分析中用同一标准正态随机变量μ来表示不同温度下材料循环应力-应变曲线的分散性。GH4133合金在250、400和500℃下疲劳试验得到的循环应力-应变数据点及对应取μ＝0、±3的循环应力-应变曲线如图1所示。可以看出,本文给出的概率模型能够较好地描述循环应力-应变曲线的分散性。

3 涡轮盘低循环疲劳可靠性设计

涡轮盘低循环疲劳寿命受到转速、温度场、材料和结构几何尺寸等随机因素的影响，而对于初步方案已经确定了发动机性能和轮盘材料的情况，转速、温度场、材料性能等的随机性已经确定，涡轮盘低循环疲劳可靠性设计的任务就是在充分考虑各随机因素影响的条件下，反复调整轮盘结构关键尺寸，使涡轮盘低循环疲劳寿命满足一定的可靠性要求。

涡轮盘低循环疲劳可靠性设计流程如下：在ANSYS平台下，利用APDL语言进行涡轮盘3维参数化建模；考虑载荷、温度、材料循环应力－应变关系和几何参数随机性，进行灵敏度分析，以确定涡轮盘结构概率分析中的关键影响参数[10]；通过涡轮盘结构低循环疲劳可靠性分析判断是否满足可靠性设计要求，并对关键几何参数进行反复改进设计，最终获得满足可靠性要求的涡轮盘结构设计。为了验证涡轮盘疲劳可靠性设计方法的可行性，下面给出了某型涡轮盘疲劳可靠性设计实例，设计目标为，通过在一定范围内调整几何结构参数使涡轮盘对应可靠度0.9987的低循环疲劳寿命不低于4000次标准循环。

3.1 涡轮盘结构参数化建模

假设某型涡轮盘结构设计初始方案已确定，利用APDL语言建立的1/12轮盘3维有限元模型如图2所示，轮心内径r0=50 mm，厚度d0=100 mm；轮缘外径r1=260 mm，厚度d1=30 mm；从轮心开始随半径r从r0增大到r2=80 mm，轮盘厚度保持不变，r从r2增大到r3=105 mm，厚度逐渐减小到d2=38 mm，r继续增大到r4=152 mm，厚度保持d2不变，r3的过渡圆角半径rf1=20 mm。为了验证APDL语言3维参数化建模的有效性，在半径r5=127.5 mm的位置均匀分布了12个半径rh=8 mm的螺栓孔。在半径r4的位置有沿径向厚度为db＝6 mm的缘板，与盘体相接位置的圆角半径均为rf2＝12 mm；缘板上侧轮盘厚度d3=30 mm，随半径增大厚度逐渐变小，到r6=225 mm处厚度最小为d4=20 mm；随着半径继续增大，轮盘厚度增大，到r7=240 mm时与外缘厚度d1相等，到轮盘外缘厚度保持不变；厚度最小处的过渡圆角半径rf3=25 mm。建模选取的几何参数和可调范围见表1。涡轮盘材料为GH4133合金，对应标准循环转速ω＝1598.8 rad/s，叶片的离心载荷折合为轮缘面载荷Pb=－159.8 MPa；温度分布用2次幂函数来模拟，如图3所示。轮心温度t0=300℃，轮缘温度t1=650℃，半径r处的温度tr为

3.2 涡轮盘结构参数灵敏度分析

根据循环应力-应变概率模型设定材料参数，并施加约束条件，求解涡轮盘的应力、应变响应。等效应力云图如图4所示，等效应变云图如图5所示。最大等效应力972.3 MPa和最大等效应变0.008073都出现在螺栓孔位置，可以确定该部位为涡轮盘低循环疲劳寿命危险点。考虑到涉及的几何参数很多，而其中有些参数可能对轮盘危险部位的应力和应变影响很小，在可靠性分析中没有必要考虑为随机变量，因此，将表1中几何参数作为可调区间内的均匀分布变量，采用Monte Carlo方法对涡轮盘危险点应变进行几何参数灵敏度分析，其结果如图6所示。

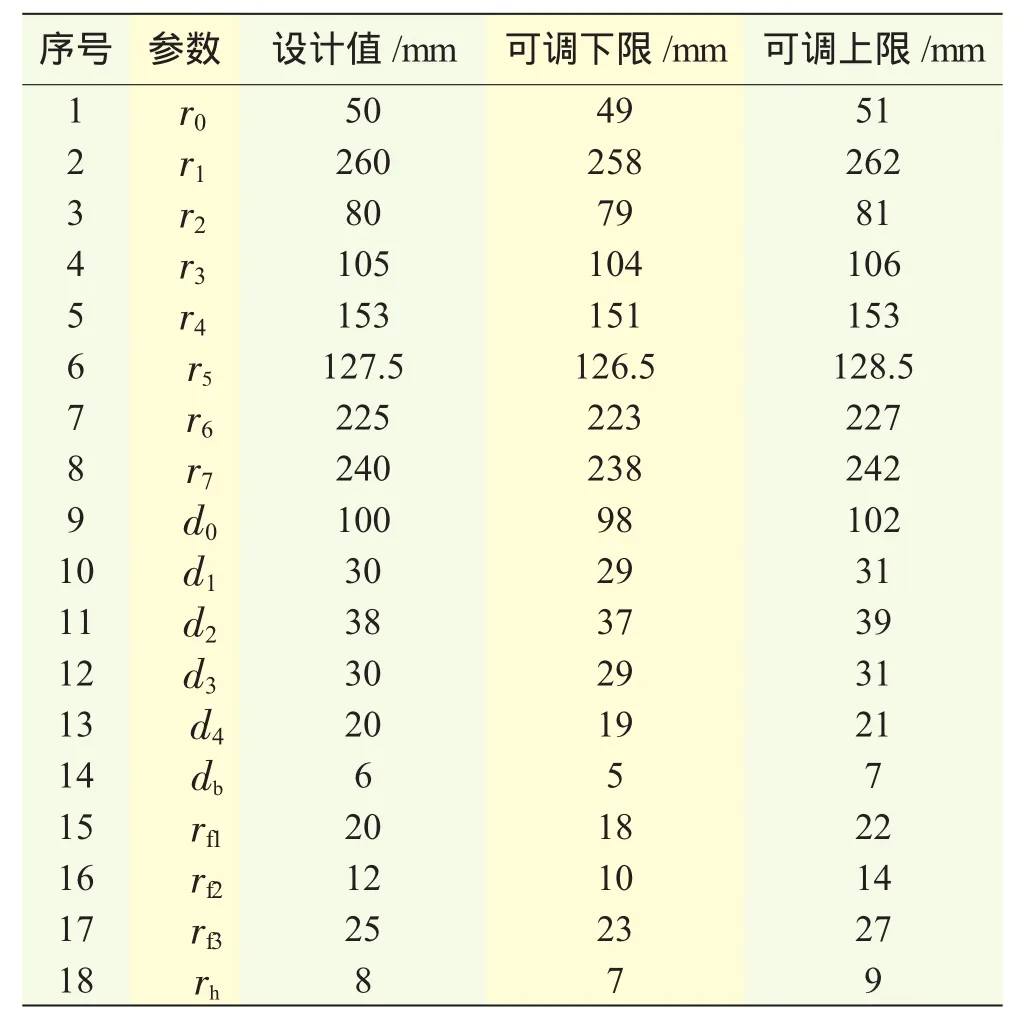
表1 几何参数和可调范围

从图6中可见，对涡轮盘危险点应变水平影响最为明显的5个几何参数为螺栓孔半径rh、径向位置r5、轮盘最小厚度d4、径向位置r7和最小厚度处的过渡圆角半径rf3，其余参数对最大应变的影响较小，在分析中可以忽略。在5个几何参数中，rh、d4、rf3增大会导致应变水平增大，r5、r7增大会导致应变水平减小。

3.3 涡轮盘疲劳寿命可靠性分析

螺栓孔位置的温度为380℃左右，由于缺少该温度下的试验数据和寿命模型，因此，在分析中采用基于线性异方差回归分析的400℃下GH4133合金循环应变－寿命概率模型[11]，平均应力修正采用Morrow修正方法。

疲劳性能参数的随机表达式为

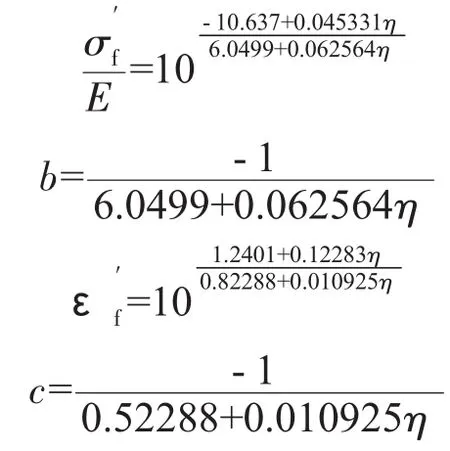
式中：η为标准正态随机变量。

在分析中选取的随机变量包括 rh、d4、rf3、r5、r7，轮盘转速ω、循环应力－应变概率模型和循环应变－寿命概率模型中的标准正态随机变量μ、η等。假设所有尺寸公差范围为±0.5 mm，即几何参数标准差均取0.5/3≈0.167 mm，轮盘转速控制精度为±1%，标准差取 0.01·ω/3≈5.33 rad/s，分析参数的均值、标准差见表2。直接采用Monte Carlo方法求解结构随机可靠性问题计算量非常大，10万次模拟大约需要2000 h以上，因此，采用响应面分析方法[5]。首先，通过79次计算拟合疲劳寿命的响应面函数；其次，对响应面函数进行10万次Monte Carlo抽样计算，统计分析得到涡轮盘危险部位的疲劳寿命分布，如图7所示，疲劳寿命的累积概率密度函数如图8所示。通过分析得出，对应可靠度水平0.9987的涡轮盘寿命为3857次循环，没有达到4000次循环的设计指标，因此需要进一步改进该涡轮盘的结构设计。

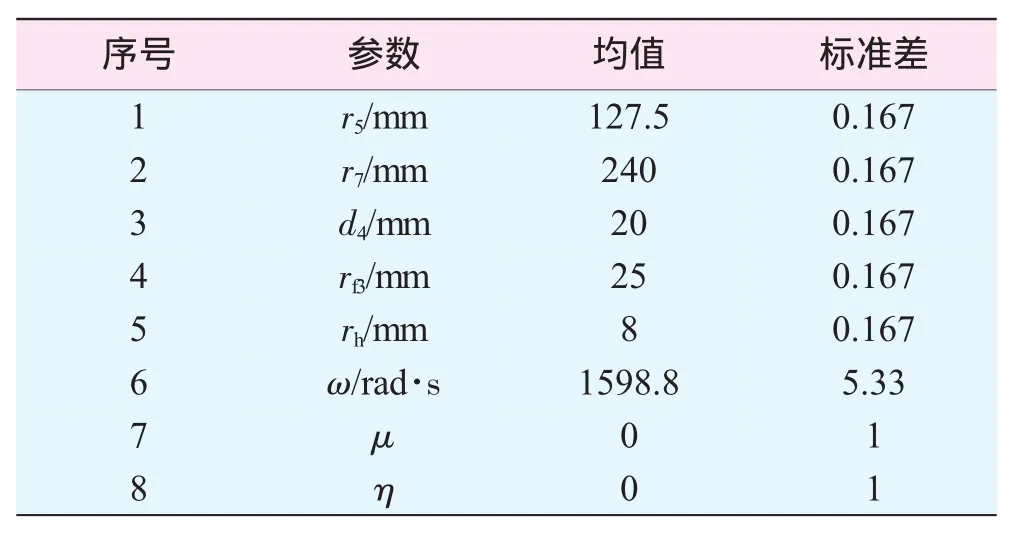
表2 可靠性分析参数

3.4 改进设计

根据设计流程，设计不能满足可靠性要求时，要返回修改结构设计，这里假设几何参数公差范围不变，即只修改几何参数的均值，标准差不变。灵敏度分析结果表明，选取的5个结构几何参数中，rh、d4、rf3增大会导致应变水平增大，r5、r7增大会导致应变水平减小。此外，还要综合考虑修改设计后轮盘体积（质量）的变化，尽量在不增大轮盘体积的条件下使涡轮盘可靠性寿命达到设计指标。经过多次修改，最终确定的几何参数见表3，此时涡轮盘对应可靠度0.9987的寿命达到4004次循环，满足设计要求，并且轮盘的体积也略有减小。

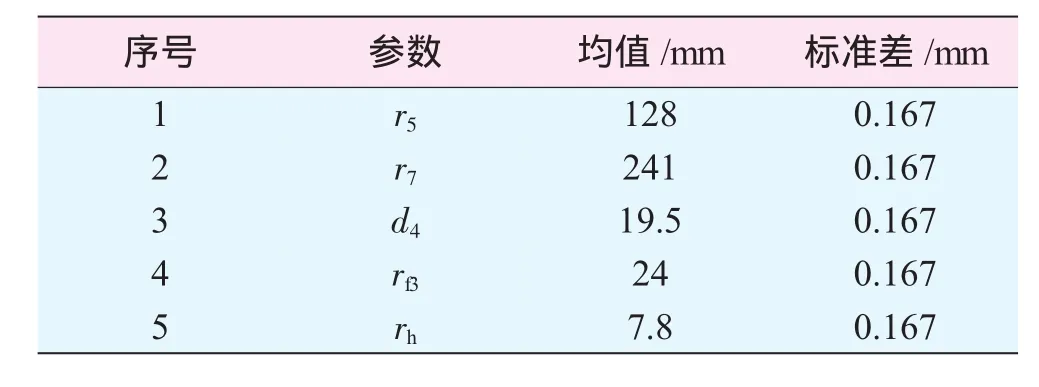
表3 几何参数最终设计值

4 结论

（1）材料循环应力－应变曲线具有明显的分散性，其分散性对结构低循环疲劳寿命具有较大影响，本文建立了循环应力－应变概率模型，并在现有试验数据基础上得到了GH4133合金在不同温度下的应力－应变概率模型。

（2）提出了涡轮盘低循环疲劳寿命可靠性设计方法，并通过算例进行了验证。

（3）采用APDL语言建立了3维参数化的涡轮盘有限元模型，通过灵敏度分析确定关键几何参数，由疲劳寿命可靠性分析得出涡轮盘的可靠性寿命，通过对几何参数的不断修改，最终实现涡轮盘的寿命可靠性设计指标。

[1]唐俊星,陆山.轮盘应变疲劳寿命可靠性分析方法[J].推进技术,2005,26(4):344-347.

[2]高阳,白广忱,张瑛莉.基于应变的结构疲劳概率寿命模型[J].航空制造技术,2008,21：82-85.

[3]高阳,白广忱,张瑛莉.涡轮盘低循环疲劳寿命的概率分析[J].航空动力学报,2009,24(4):804-809.

[4]高阳,白广忱,张瑛莉.涡轮盘多轴低循环疲劳寿命可靠性分析[J].航空学报,2009,30(9):1678-1682.

[5]李辉,白广忱.基于响应面法的涡轮盘低循环疲劳可靠性分析方法[J].航空发动机,2008,34(1):28-30.

[6]蒋向华,杨晓光,王延荣.结构可靠度逐步逼近径向基神经网络响应面法[J].航空动力学报,2008,23(1):26-31.

[7]高阳,白广忱,于霖冲.基于RBF神经网络的涡轮盘疲劳可靠性分析[J].机械设计,2009,26(5):8-10.

[8]高阳.航空发动机涡轮盘低循环疲劳可靠性分析[D].北京航空航天大学博士学位论文.北京：北京航空航天大学，2009.

[9]王卫国.轮盘低循环疲劳寿命预测模型和试验评估方法研究[D].南京：南京航空航天大学,2006.

[10]Wesley Osborn R,Harry R.Millwater.Application of Probabilistic Sensitivities in Probabilistic Fatigue Analysis ofGas Turbine Engine Disks[C].46th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics＆amp;Materials confer,Austin,Texas,2005.

[11]高阳,白广忱.轮盘低循环疲劳寿命可靠性分析方法[J].机械设计与制造,2009(6):60-62.